При встановленні діагнозу і проведенні лікування лікарі все більше покладаються на медичні зображення, до яких відносяться рентгенограми, УЗІ, магнітно-резонансна томографія (MRI - Magnetic Resonance Imaging), комп'ютерна томографія (CT - Computed Tomography), томографія на позитивному випромінюванні (PET - Positive Emission Tomography) тощо. Використання медичних зображень зростає з кожним роком, внаслідок впровадження новітньої медичної техніки в лікарнях і діагностичних центрах. Об'єкти на медичних зображеннях володіють великою складністю і багатофакторністю, що зумовлює високі вимоги до надійності, точності та достовірності результатів досліджень. Швидкий розвиток цифрової і аналогової техніки останнім часом відкриває нові можливості перед розробниками. Наприклад, збільшення швидкодії обчислювальної техніки дозволяє використовувати складні, критичні до часу алгоритми, а завдяки появі кольорових телевізійних датчиків високого дозволу можна отримувати і обробляти кольорові зображення. Саме нові технічні можливості дозволяють значно розширити коло досліджень, відкривають нові шляхи вирішення завдань, що стосуються аналізу зображень.

     На сьогоднішній день дуже великий обсяг медичної інформації міститься у всіляких знімках. Знімки володіють різною складністю і многофактурностью [2], постійно виникає завдання точного пошуку об'єктів і меж об'єктів на представлених знімках для точного встановлення діагнозу. Дану задачу можна вирішувати з допомогою методів цифрового аналізу зображень. Сегментація є завданням складним, методи для вирішення завдання кожного разу вибираються різні, все залежить від характеристик і властивостей аналізованого зображення.

     Алгоритм мурашиних колоній (ACO) - застосовується в багатьох задачах оптимізації і показує добрі результати роботи. При застосуванні його до задачі сегментації ми отримуємо ефективність. На сьогоднішній день подібні розробки ведуться, але до практичного впровадження ще необхідні додаткові дослідження та результати.

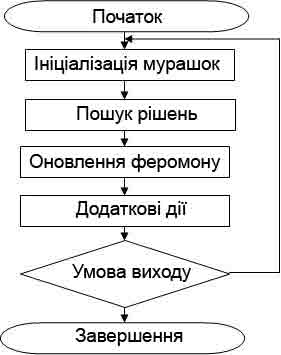
Рисунок 1 - Загальний вигляд алгоритму мурашиних колоній

     Для того, щоб побудувати відповідний мурашиний алгоритм для вирішення якої-небудь задачі, необхідно [4]:

1. Представити задачу у вигляді набору компонент і переходів або набором неорієнтованих зважених графів, на яких мурахи можуть будувати рішення.

2. Визначити значення сліду феромона.

3. Визначити евристику поведінки мурашки, коли будуємо рішення.

4. Якщо можливо, то реалізувати ефективний локальний пошук

5. Вибрати специфічний ACO алгоритм і застосувати для розв'язання задачі.

6. Налаштувати параметр ACO алгоритму

Також визначальними є:

• кількість мурашок;
• баланс між вивченням та використанням;
• поєднання з жадібними евристиками або локальним пошуком;
• момент, коли оновлюється феромон.

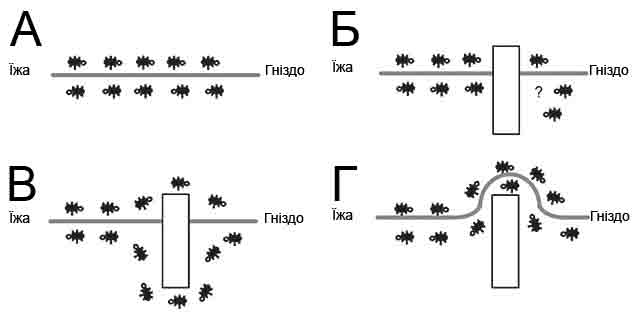
Рисунок 2 - Пошук мурашками шляху від гнізда до джерела їжі

     Алгоритм мурашиних колоній будемо використовувати разом з методом кластеризації k-середніх, для збільшення ефективності сегментації зображень [2]. Розроблюваний змішаний алгоритм почнемо з вибору кількості кластерів і випадковим чином инициализируем їх центри. Тепер, згідно з алгоритмом кластеризації к-середніх ми повинні визначити приналежність кожного пікселя зображення певного кластеру. На цьому етапі найважливішу роль відіграє алгоритм мурашиних колоній він визначає зв'язок кожного пікселя з кластерами зображення. Це виконується згідно ймовірності, яка обернено пропорційна відстані між пікселом і центром кластера та змінної t, яка представляє рівень феромону. Рівень феромона визначаємо пропорційно мінімального відстані між кожною парою центрів кластерів і назад пропорційно відстані між кожним кожним пикселом і його центром. Таким чином, значення рівня феромона зростає із збільшенням дистанції між центрами кластерів і при більшій компактності пікселів в кластере.Прі цих же умовах зростає і ймовірність приєднання пікселя до кластеру [5].
     Випаровування феромона розраховується для того, щоб послабити вплив попередніх вибраних рішень, які є менш пріоритетними. Аналогічно алгоритму к-середніх, в розподіленому стані відбувається оновлення кластерних центрів, шляхом перерахунку середнього значення пікселів в кожному кластері і це продовжується до тих пір, поки зміна значення кластерного центру суттєво не змінюється. На відміну від алгоритму к-середніх, що розробляється метод не зупиняється на цьому етапі. Процес кластеризації продовжують виконувати m мурашок, кожен з яких в кінцевому підсумку знаходить рішення. Критерій знаходження кращого рішення і оновлений рівень феромону відповідно для наступної групи m мурашок є провідними для наступної групи. При виконанні критерію зупину кластеризація завершується Таким чином, краще рішення знайдено.
     Алгоритм починається з визначення рівня феромона t і завдання евристичної інформації h для кожного пікселя. Потім, кожен мураха визначає приналежність пікселя кластера з імовірністю P, яка розраховується з виразу (3.1):

(3.1)

де 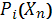- вірогідність належності пікселя кластеру i, і - і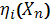нформація про феромон та евристична змінна належності пікселя кластеру i відповідно, 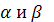- постійні параметри, які визначають відносний вплив феромона та евристичної інформації, К – кількість кластерів. Евристична інформація 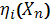обчислюється згідно з виразом (3.2):

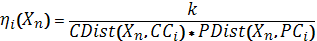
(3.2)

де 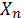- піксель номер n, - i-тый спектральний кластерний центр і 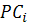– i-ий просторовий центр кластера. 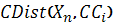- відстань між 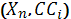відповідно до кольорових характеристик пікселів і - евклідова відстань між , відповідно розташування пікселя на зображенні. Константа k використовується для балансування значень n і t.Значення рівня феромонів на початковому етапі встановлюється рівним 1, тому на першій ітерації він не впливає на ймовірність переходу.

     Припустимо m - кількість мурашок, обраних для кластеризації зображення. Кожен мураха знаходить своє індивідуальне рішення задачі. Після того, як m мурах сегментували зображення, вибирається краще рішення для поточної ітерації, для нього инкрементируется рівень феромону і відбувається оновлення всіх центрів кластерів відповідно до обраного кращому вирішенню. На наступній ітерації ініціалізація мурашок відбувається відповідно до попереднього досвіду. На кожній ітерації кожен з m мурах знаходить індивідуальне рішення, яке коригується власними евристичними знаннями, загальним кращим рішенням, знайденим усіма мурахами. Це повторюється, поки буде знайдено рішення, яке задовольняє всім заданим умовам. Загальне рішення з m індивідуальних рішень вибирається згідно 2 параметрів:

1. Евклідова відстань між кластерними центрами виходячи з колірних характеристик (відособленість кластерів).

2. Сума евклідова відстаней між центром кластера і кожним його пікселем згідно колірних і просторових характеристик (схожість та компактність кластерів).

Щоб вибрати найкраще рішення з усіх локальних необхідно, щоб виконувалися наступні умови:

1. Евклідова відстань між кластерними центрами виходячи з колірних характеристик (відособленість кластерів)

2. Сума евклідова відстаней між центром кластера і кожним його пікселем згідно колірних і просторових характеристик (схожість та компактність кластерів).

3. Сума евклідова відстаней між центром кластера і кожним його пікселем згідно просторових характеристик повинна бути маленькою, відповідно кластери будуть більш компактними.

Рисунок 3 - Сегментація зображення алгоритмом к-середніх

     Для того, щоб виконати першу умову, ми розраховуємо для кожного мурашки відстані між кожною парою центрів кластерів і сортуємо їх. Потім вибираємо мінімальні серед всіх мурах і порівнюємо їх, вибираючи максимальний [MinMax (k)].
     Для виконання пунктів 2 і 3 необхідно підрахувати суми відстаней між кластерними центрами та їхньою пікселями, потім відсортувати. Вибрати максимальне для кожного мурашки і мінімальне з цих значень. Кожного разу вибране значення отримує додатковий пріоритет. Саме пріоритетне є кращим. Після того як вибрано краще рішення оновлюється значення рівня феромона відповідно до виразу (3.3):

(3.3)

де коефіцієнт випаровування 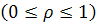, який впливає на раніше встановлений рівень феромону. Завдяки цьому коефіцієнту посилюється вплив більш пізніх пріоритетних рішень і послаблюється більш ранніх. Параметр 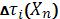у виразі (3.3) – різниця рівня феромона, яка додається до попередньої успішним мурахою. Вона обчислюється відповідно до [3]:

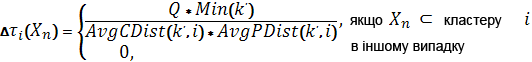(3.4)

де Q - позитивна константа, яка пов'язана з величиною доданого мурахами феромона, - мінімальне з колірних дистанцій між кожними двома центрами кластерів, знайдене мурахою k '(найуспішнішим мурахою). AvgCDist (k ', i) - середнє з колірних евклідова відстаней і AvgPDist (k', i) - середнє з просторових евклідова відстаней між кожним пікселем і центрами (колірним і просторовим) для самого успішного мурахи. Min (k') - причина збільшення феромона при більшій віддаленості кластерів. AvgCDist (k', i) і AvgPDist (k', i) - причини збільшення рівня феромона при більшій однорідності і компактності кластеру.      Змішаний алгоритм мурашиних колоній і к-середніх далі представлений покроково [5]:

1. Ініціалізіруем основні параметри алгоритму: значення рівня феромонів на першому етапі вважаємо рівним 1, кількість кластерів К, кількість мурашок m.

2. Ініціалізіруем m мурашок для К случаймо вибраних центрів кластерів.

3. Нехай кожен мураха пов'язує кожен піксель з одним із кластерів i, випадковим чином, з імовірністю з виразу (3.1).

4. Обчислюємо нові центри кластерів. Якщо нові центри збігаються з попередніми, то переходимо до наступного кроку, якщо ні, переходимо до пункту 3.

5. Зберігаємо краще рішення з усіх знайдених m мурахами.

6. Оновлюємо рівень феромону для кожного пікселя згідно 3.3 та 3.4

7. Коригуємо загальне краще рішення виходячи зі знайдених індивідуальних рішень кожного мурахи.

8. Якщо виконується критерій зупину, то переходимо до наступного кроку. У зворотному випадку, переходимо до пункту 3.

9. Знайдено спільне краще рішення.

Рисунок 4 - Приклад сегментації зображення

Висновок

     Хоча алгоритми обробки зображень можуть забезпечити одержання точних кількісних показників (наприклад, вимір фракції викиду лівого шлуночка серця по динамічній послідовності зображень) або можуть вирішувати деякі завдання, які нездійсненні при ручній обробці (наприклад, точна реєстрація мультимодальних зображень), проблеми надійності та відповідальності залишаються головними перешкодами на шляху широкомасштабного використання цих алгоритмів. Перевірка правильності алгоритму часто буває скрутна через відсутність теорії, що дозволяє кількісно порівнювати результати обробки.

Література

1. Вадим Конушин, Владимир Вежневец,Методы сегментации изображений: интерактивная сегментация, // Вестник МГУ им Ломоносова – №4, 2008. – С. 107-118

2. L. Lucchese and S.K. Mitra “Color Image Segmentation: A State-of-the-Art Survey”, 2001

3. N. R. Pal and S. K. Pal, “A Review on Image Segmentation Techniques,” Pattern Recognition, Vol. 26, No 9, 2000

4. R. Laptik, D. Navakauskas, Application of Ant Colony Optimization for Image Segmentation [Електроний ресурс]. - Режим доступа: http://www.ktu.lt/lt/mokslas/zurnalai/elektros_z/....

5. Ruobing Zou, Weiyu Yu, Image Segmentation Based on Local Ant Colony Optimization [Електроний ресурс]. - Режим доступа: http://www.computer.org/portal/web/csdl/....

6. Ахметшин А.М., Ахметшина Л.Г., Сегментация низкоконтрастных медицинских радиологических изображений методом пространственно-резонансного отображения [Электронный ресурс]. - Режим доступа: http://www.uacm.kharkov.ua/download/....

7. Tomas Piatrik, Ebroul Izquierdo, An application of ant colony optimization to image clustering [Электронный ресурс]. - Режим доступа: http://citeseerx.ist.psu.edu/....

8. Dzung L.Pham, Chenyang Xu, Jerry L.Prince, A survey of current methods in medical image segmentation [Электронный ресурс]. - Режим доступа: http://www.mcs.csueastbay.edu/....

9. Huizhi Cao, Peng Huang, Shuqian Luo, A novel image segmentation algorithm based on artificial ant colonies [Электронный ресурс]. - Режим доступа: http://books.google.ru/....

10. Myung-Eun Lee, Soo-Hyung Kim, Wan-Hyun Cho, Soon-Young Park, Jun-Sik Lim, Segmentation of Brain MR Images Using an Ant Colony Optimization Algorithm [Электронный ресурс]. - Режим доступа: http://www.computer.org/....

Важливе зауваження

     При написанні цього автореферату магістерська робота ще не завершена. Остаточне завершення: 1 грудня 2011 р. Повний текст роботи та матеріали за темою можуть бути отримані у автора або його керівника після зазначеної дати.