При установлении диагноза и проведении лечения врачи все больше полагаются на медицинские изображения, к которым относятся рентгенограммы, УЗИ, магнитно-резонансная томография (MRI - Magnetic Resonance Imaging), компьютерная томография (CT - Computed Tomography), томография на позитивном излучении (PET – Positive Emission Tomography) и т.д. Использование медицинских изображений растет с каждым годом, вследствие внедрения новейшей медицинской техники в больницах и диагностических центрах. Объекты на медицинских изображениях обладают большой сложностью и многофакторностью, что обусловливает высокие требования к надёжности, точности и достоверности результатов исследований. Быстрое развитие цифровой и аналоговой техники в последнее время открывает новые возможности перед разработчиками. Например, увеличение быстродействия вычислительной техники позволяет использовать сложные, критичные ко времени алгоритмы, а благодаря появлению цветных телевизионных датчиков высокого разрешения можно получать и обрабатывать цветные изображения. Именно новые технические возможности позволяют значительно расширить круг исследований, открывают новые пути решения задач, касающихся анализа изображений.

     На сегодняшний день очень большой объем медицинской информации содержится во всевозможных снимках. Снимки обладают различной сложностью и многофактурностью [2], постоянно возникает задача точного поиска объектов и границ объектов на представленных снимках для точной постановки диагноза. Данную задачу можно решать с помощью методов цифрового анализа изображений. Сегментация является задачей сложной, методы для решения задачи каждый раз выбираются разные, все зависит от характеристик и свойства анализируемого изображения.

     Алгоритм муравьиных колоний(ACO) – применяется во многих задачах оптимизации и показывает хорошие результаты работы. При применении его к задаче сегментации мы получаем эффективность. На сегодняшний день подобные разработки ведутся, но до практического внедрения еще необходимы дополнительные исследования и результаты.

Рисунок 1 - Общий вид алгоритма муравьиных колоний

     Для того чтобы построить подходящий муравьиный алгоритм для решения какой-либо задачи, необходимо[4]:

1. Представить задачу в виде набора компонент и переходов или набором неориентированных взвешенных графов, на которых муравьи могут строить решения.

2. Определить значение следа феромона.

3. Определить эвристику поведения муравья, когда строим решение.

4. Если возможно, то реализовать эффективный локальный поиск

5. Выбрать специфический ACO алгоритм и применить для решения задачи.

6. Настроить параметр ACO алгоритма

Также определяющими являются:

• количество муравьёв;
• баланс между изучением и использованием;
• сочетание с жадными эвристиками или локальным поиском;
• момент, когда обновляется феромон.

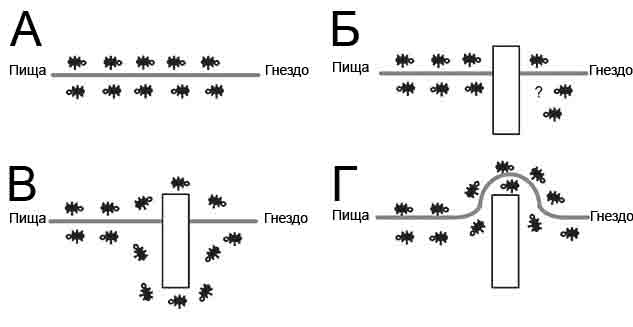
Рисунок 2 - Поиск муравьями пути от гнезда до источника пищи

     Алгоритм муравьиных колоний будем использовать совместно с методом кластеризации k-средних, для увеличения эффективности сегментации изображений[2]. Разрабатываемый смешанный алгоритм начнем с выбора количества кластеров и случайным образом инициализируем их центры. Теперь, согласно алгоритму кластеризации к-средних мы должны определить принадлежность каждого пикселя изображения определенному кластеру. На этом этапе самую важную роль играет алгоритм муравьиных колоний он определяет связь каждого пикселя с кластерами изображения. Это выполняется согласно вероятности, которая обратно пропорциональна расстоянию между пикселом и центром кластера и переменной t, которая представляет уровень феромона. Уровень феромона определяем пропорционально минимальному расстоянию между каждой парой центров кластеров и обратно пропорционально расстоянию между каждым каждым пикселом и его центром. Таким образом, значение уровня феромона растет с увеличением дистанции между центрами кластеров и при большей компактности пикселей в кластере.При этих же условиях возрастает и вероятность присоединения пикселя к кластеру[5].
     Испарение феромона рассчитывается для того, чтобы ослабить воздействие предыдущих выбранных решений, которые являются менее приоритетными. Аналогично алгоритму к-средних, в распределенном состоянии происходит обновление кластерных центров, путем пересчета среднего значения пикселей в каждом кластере и это продолжается до тех пор, пока изменение значения кластерного центра существенно не меняется. В отличие от алгоритма к-средних, разрабатываемый метод не останавливается на этом этапе. Процесс кластеризации продолжают выполнять m муравьев, каждый из которых в конечном итоге находит решение. Критерий нахождения лучшего решения и обновленный уровень феромона соответственно для следующей группы m муравьев являются ведущими для следующей группы. При выполнении критерия останова кластеризация завершается Таким образом, лучшее решение найдено.
     Алгоритм начинается с определения уровня феромона t и задания эвристической информации h для каждого пикселя. Затем, каждый муравей определяет принадлежность пикселя кластера с вероятностью P, которая рассчитывается из выражения (3.1):

(3.1)

где - вероятность принадлежности пикселя кластеру i, и - информация о феромоне и эвристическая переменная принадлежности пикселя кластеру i соответственно, - константные параметры, которые определяют относительное влияние феромона и эвристической информации, К – количество кластеров. Эвристическая информация вычисляется согласно выражению (3.2):

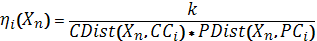
(3.2)

где - пиксель номер n, - i-тый спектральный кластерный центр и – i-тый пространственный центр кластера. - расстояние между согласно цветовым характеристикам пикселей и - эвклидово расстояние между , согласно расположения пикселя на изображении. Константа k используется для балансировки значения n с t.Значение уровня феромона на начальном этапе устанавливается равным 1, поэтому на первой итерации он не оказывает влияние на вероятность перехода.

     Предположим m – количество муравьев, выбранных для кластеризации изображения. Каждый муравей находит свое индивидуальное решение задачи. После того, как m муравьев сегментировали изображение, выбирается лучшее решение для текущей итерации, для него инкрементируется уровень феромона и происходит обновление всех центров кластеров согласно выбранному лучшему решению. На следующей итерации инициализация муравьев происходит согласно предыдущему опыту. На каждой итерации каждый из m муравьев находит индивидуальное решение, которое корректируется собственными эвристическими знаниями, общим лучшим решением, найденным всеми муравьями. Это повторяется, пока будет найдено решение, удовлетворяющее всем заданным условиям. Общее решение из m индивидуальных решений выбирается согласно 2 параметров:

• Эвклидово расстояние между кластерными центрами исходя из цветовых характеристик (обособленность кластеров)

• Сумма Эвклидовых расстояний между центром кластера и каждым его пикселем согласно цветовых и пространственных характеристик (похожесть и компактность кластеров).

Чтобы выбрать лучшее решение из всех локальных необходимо, чтобы выполнялись следующие условия:

• Эвклидово расстояние между кластерами с точки зрения цветовых характеристик должно быть велико, соответственно кластеры будут отличными друг от друга.

• Сумма эвклидовых расстояний между центром кластера и каждым его пикселем согласно цветовых характеристик должна быть маленькой, соответственно кластер будет более однородным.

• Сумма эвклидовых расстояний между центром кластера и каждым его пикселем согласно пространственных характеристик должна быть маленькой, соответственно кластеры будут более компактными.

Рисунок 3 - Сегментация изображения алгоритмом к-средних

     Для того, чтобы выполнить первое условие, мы рассчитываем для каждого муравья расстояния между каждой парой центров кластеров и сортируем их. Затем выбираем минимальные среди всех муравьев и сравниваем их, выбирая максимальный [MinMax(k)].
     Для выполнения пунктов 2 и 3 необходимо подсчитать суммы расстояний между кластерными центрами и их пикселями, затем отсортировать. Выбрать максимальное для каждого муравья и минимальное из этих значений. Каждый раз выбранное значение получает дополнительный приоритет. Самое приоритетное является лучшим. После того как выбрано лучшее решение обновляется значение уровня феромона согласно выражению (3.3):

(3.3)

где коэффициент испарения , который воздействует на ранее установленный уровень феромона. Благодаря этому коэффициенту усиливается влияние более поздних приоритетных решений и ослабляется более ранних. Параметр в выражении (3.3) – разница уровня феромона, которая добавляется к предыдущей успешным муравьем. Она вычисляется согласно[3]:

(3.4)

где Q – положительная константа, которая связана с величиной добавленного муравьями феромона, - минимальное из цветовых дистанций между каждыми двумя центрами кластеров, найденное муравьем k’ (самым успешным муравьем). AvgCDist(k',i) – среднее из цветовых эвклидовых расстояний и AvgPDist(k',i) – среднее из пространственных эвклидовых расстояний между каждым пикселем и центрами(цветовым и пространственным) для самого успешного муравья. Min(k') – причина увеличения феромона при большей отдаленности кластеров. AvgCDist(k',i) и AvgPDist(k',i) – причины увеличения уровня феромона при большей однородности и компактности кластера.      Смешанный алгоритм муравьиных колоний и к-средних далее представлен пошагово[5]:

1. Инициализируем основные параметры алгоритма: значение уровня феромона на первом этапе полагаем равным 1, количество кластеров К, количество муравьев m.

2. Инициализируем m муравьев для К случаймо выбранных центров кластеров.

3. Пусть каждый муравей связывает каждый пиксель с одним из кластеров i, случайным образом, с вероятностью из выражения (3.1).

4. Вычисляем новые центры кластеров. Если новые центры совпадают с предыдущими, то переходим к следующему шагу, если нет, переходим к пункту 3.

5. Сохраняем лучшее решение из всех найденных m муравьями.

6. Обновляем уровень феромона для каждого пикселя согласно 3.3 и 3.4

7. Корректируем общее лучшее решение исходя из найденных индивидуальных решений каждого муравья.

8. Если выполняется критерий останова, то переходим к следующему шагу. В обратном случае, переходим к пункту 3.

9. Найдено общее лучшее решение.

Рисунок 4 - Пример сегментации изображения

Вывод

     Хотя алгоритмы обработки изображений могут обеспечить получение точных количественных показателей (например, измерение фракции выброса левого желудочка сердца по динамической последовательности изображений) или могут решать некоторые задачи, которые невыполнимы при ручной обработке (например, точная регистрация мультимодальных изображений), проблемы надежности и ответственности остаются главными препятствиями на пути широкомасштабного использования этих алгоритмов. Проверка правильности алгоритма часто бывает затруднительна из-за отсутствия теории, позволяющей количественно сравнивать результаты обработки.

Литература

1. Вадим Конушин, Владимир Вежневец,Методы сегментации изображений: интерактивная сегментация, // Вестник МГУ им Ломоносова – №4, 2008. – С. 107-118

2. L. Lucchese and S.K. Mitra “Color Image Segmentation: A State-of-the-Art Survey”, 2001

3. N. R. Pal and S. K. Pal, “A Review on Image Segmentation Techniques,” Pattern Recognition, Vol. 26, No 9, 2000

4. R. Laptik, D. Navakauskas, Application of Ant Colony Optimization for Image Segmentation [Электронный ресурс]. - Режим доступа: http://www.ktu.lt/lt/mokslas/....

5. Ruobing Zou, Weiyu Yu, Image Segmentation Based on Local Ant Colony Optimization [Электронный ресурс]. - Режим доступа: http://www.computer.org/portal/web/csdl/....

6. Ахметшин А.М., Ахметшина Л.Г., Сегментация низкоконтрастных медицинских радиологических изображений методом пространственно-резонансного отображения [Электронный ресурс]. - Режим доступа: http://www.uacm.kharkov.ua/download/....

7. Tomas Piatrik, Ebroul Izquierdo, An application of ant colony optimization to image clustering [Электронный ресурс]. - Режим доступа: http://citeseerx.ist.psu.edu/....

8. Dzung L.Pham, Chenyang Xu, Jerry L.Prince, A survey of current methods in medical image segmentation [Электронный ресурс]. - Режим доступа: http://www.mcs.csueastbay.edu/....

9. Huizhi Cao, Peng Huang, Shuqian Luo, A novel image segmentation algorithm based on artificial ant colonies [Электронный ресурс]. - Режим доступа: http://books.google.ru/....

10. Myung-Eun Lee, Soo-Hyung Kim, Wan-Hyun Cho, Soon-Young Park, Jun-Sik Lim, Segmentation of Brain MR Images Using an Ant Colony Optimization Algorithm [Электронный ресурс]. - Режим доступа: http://www.computer.org/....

Важное замечание

     При написании данного автореферата магистерская работа еще не завершена. Окончательное завершение: 1 декабря 2011 г. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.