Lehrstelle:
Thema von Masterarbeit:
Betreuer: Prof. Dr.-Ing. Volodymyr Svjatnyj |
Kontakte:
|
Referat
Thema: Ausarbeitung und Untersuchung des Subsystems von parallelen Gleichungloesern der verteilten parallelen Simulationsumgebung (VPSU)
Ziel der Arbeit:
Forschung, Entwicklung und Implementierung des Subsystems von parallelen Gleichungslösern in Rahmen von virtueller paralleler Simulationsumgebung.
Arbeitsaufgaben:
Im Rahmen der Meisterarbeit sind solche Probleme zu lösen:
- Überprüfung der Arbeiten, die in Richtung der parallelen verteilten Simulationsumgebungen (VPSU) und parallelen Gleichungslösern insbesondere durchgeführt sind.
- Definition der Funktionen und Struktur des Subsystems von Gleichungslösern.
- Es ist ein Testlöser zu entwickeln – MIMD-Oszillator.
- Es ist ein MIMD-Löser des Koshiproblems zu realisieren, der sich auf blockartigen numerischen Verfahren basiert.
- Man muss eine System-Software Implementierung des Subsystems von Gleichungslösern im Rahmen VPSU geben.
Wissenschaftliche Neuheit der Arbeit:
- Implementierung von Algorithmen der parallelen Gliechungslöser und ihre Anwendung als separates Subsystem in VPSU.
- Realisierung und Einführung in VPSU eines MIMD-Lösers, der sich auf blockartigen numerischen Verfahren basiert.
- Entwicklung und Einführung in VPSU eines MIMD-Oszillators, der als ein Effizienztester vom Computing-System verwendet werden kann.
Arbeitsaktualität
Heute ist durch ein schnelles Wachstum der verschiedenen Technologien charakterisiert. Was war ein paar Jahre relevant, ist jetzt vielleicht nur unnötig. Deshalb können wir sicher sagen, dass jetzt auf ersten Plan Modellierung kommt, die noch in der Entwurfsphase die optimalen Parameter des zukünftigen Geräts bestimmen, versteckte Mängel aufspüren und das Verhalten in bestimmten Bedingungen bewerten kann. Ein gutes Modell vergrößert die Zeit, wenn ein Produkt auf dem Markt noch aktuell ist. Je mehr Produktion man produziert, desto größere Rolle spielt Modellierung. Zum Beispiel, bei der Projektierung von automatisierten technischen Anlagen, Verarbeitungsbetrieben und Leitungen, die als komplexe dynamische Systeme (KDS) definiert sind, kommt sie auf den Vordergrund.
Seit Mitte der 80en Jahre begann ein intensiver Übergang zur digitalen Simulationen von KDS: die sequentielle Block und Gleichung orientierte Modellierungssprache wurden entwickelt und implementiert (ISRSIM, ACSL, Simulink, DYMOLA u.a.), schnell wächst Hardware-und Software-Basis von Modellierung – PCs, Parallel-Computing, SIMD- und MIMD-Architekturen, Sprachen, Bibliotheken und Standard paralleler und verteilter Programmierung. In entwickelten Ländern werden ganze Super-Rechnen-Zentren gebaut (HPCC - High Performance Computer Center), neue Fachbereiche und Institute der parallelen und verteilten Berechnungen werden gegründet.
Lätze Zeit entstehen neue Richtungen von Entwicklungen und Forschungsergebnissen – parallele Simulation (Parallel Simulation Technology, Parallele Simulationstechnik), geografisch verteilte Simulation, die sich auf GRID-Technologien basiert. Zentrales Problem der parallelen Simulation komplexer dynamischer Systeme ist die Konstruktion der verteilten parallelen Simulationsumgebungen (VPSU), wo paralleler Gleichungslöser eine Schlüsselrolle spielt.
Die Analyse der Entwicklung von VPSU und parallelen Gleichungslösern
Konzeption der verteilten parallelen Simulationsumgebung (VPSU) für komplexe dynamische Systeme mit konzentrierten und verteilten Parametern war im Jahr 1992 im Rahmen der wissenschaftlichen Zusammenarbeit zwischen Fakultät der Rechentechnik und der Informatik (FRTI, DonNTU) und Institut für Parallele und Verteilte Systeme (IPVS) der Universität Stuttgart (Deutschland) in ASIM-Bericht veröffentlicht [2] und in Arbeiten [3,4,9] weiter entwickelt.
Das Problem von VPSU-Entwicklung befindet sich in dem Staatsprogramm der Ukraine „Entwicklung wettbewerbsfähiger Modellierung komplexer Systeme“. In diesem Thema schreibt man Studenten-, Kurse-, Diplom- und Masterarbeiten.
Es gibt Zusammenarbeit mit Institut für Simulation und Graphik (ISG) der Universität Magdeburg in Fragen der Entwicklung von MIMD-Komponente problem-orientierter Umgebung, die sich auf einem Cluster von parallelen Computern basiert. Entwicklung von problem-orientierten Umgebungen wird mit Institut für Systemdynamik und Regelungstechnik (ISR, Universität Stuttgart), Max-Planck-Institut für Dynamik komplexer technischer Systeme (Magdeburg) und Unternehmen "Azot" (Sewerodonezk) durchgeführt. Das Problem der Integration von CAD-Modellierung mit Simulationsumgebungen wird zusammen mit Institut für Automatisierungs-und Softwaretechnik (IAS) der Universität Stuttgart untersucht.
Mit der Unterstützung des Bundesministeriums für Bildung und Forschung (BMBF, Deutschland) und der Universität Erlangen hat Fakultät der Rechentechnik und der Informatik (FRTI, DonNTU) die Forschung über Konzeption von automatisierten Systemen zur Unterstützung der DSVP (Projekt PROAUT) durchgeführt. Ein großes technisch orientiertes Forschungsprojekt ist die Entwicklung vom Modellierungs- und Service-Center für den Steinkohlenbergbau in der Ukraine [8].
Experimentelle Modelle von VPSU wurden auf der Grundlage des fernen Zutrittes zu parallelen Ressourcen der Universität Stuttgart gebaut. Während dieser Zeit bekamen DonNTU-Mitarbeiter praktische Erfahrung in Realisierung von parallelen Modellen auf solchen Systemen, als MasPar (16K Prozessor-Elemente), Intel Paragon, Cray T3E.
Seit Dezember 2005 kann VPSU die Ressourcen vom System NEC SX8 benutzen, das in High Performance Computing Center Stuttgart (HLRS) ist, wo schon heute man NEC SX9, Cray XT5m und CRAY XE6 verwendet. Seit 2009 hat die Fakultät für Informatik und Technologie ein paralleles MPI-Cluster NeClus (100 Knoten) in Betrieb gesetzt.
Konzept der VPSU
Verteilte parallele Simulationsumgebung (VPSU) – eine systematische Organisation von gemeinsamen Betrieb der parallelen Hardware-Ressourcen, System-Modellierung und Software, die alle Phasen der Entwicklung, Umsetzung und Anwendung der parallelen Modellen von KDS gemäß bestimmten Bedingungen stützt[1,2].
Die wichtigste Bestimmung des VPSU-Konzepts ist die Notwendigkeit voll funktionsfähige parallele Algorithmen und Methoden, Modellierungs-Software (Modellierung und Simulation-Software) für DSKP, DSVP zu entwickeln. Die Analyse zeigt, dass die parallele und SIMD-, MIMD-Strukturen 90er Jahren die spezielle Sprachen der parallelen Programmierung hatten, die auf Sprachen Fortran, C, C + +, Modula-2 und so weiter basiert wurden. Intensive Entwicklung von parallele Rechnersystemen der MIMD-Architektur, objekt-orientierte Ansätze stimulierten die Standardisierung von paralleler und verteilter Programmierung. So definiert ANSI und ISO C++-Standard mit MPI-, PVM- und Pthreads-Bibliotheken [5].
Das Konzept sieht vor, den Nutzern und Entwicklern von parallelen Modellen die Sprache und System-Tools geben, die in Fragen des Services besser werden, als fünfte Generations der Modellierungssprache. In dieser Richtung gibt es Arbeiten, die sich mit einer Verallgemeinerung der KDS-Topologie beschäftigen. Komplexe "Topologische Analysatoren - Gleichungsgeneratoren - Löser" wandeln Beschreibungen der KDS-Ebene in parallele Programme um.
In der realisierten VPSU ist die Kontinuität mit früheren Generationen von Simulation vorgesehen, die heute in SISD-Strukturen von Computer implementiert sind. Gleiche Situation ist mit der Parallelisierung der numerischen Verfahren. VPSU ist heute nicht so erforschtes Thema. Ein Beitrag hier wird von Professor Svyatny V.A. vorgeschlagen. Er schlägt die Zersetzung von Umgebung in funktionsvolle Subsysteme vor. Diese Subsysteme sollen mit GRID-Systemen verbunden sein.
Definition des Gleichungslöser-Subsystems
Universelle und problemorientierte VPSU verwendet man effektiv für die Modellierung komplexer dynamischer Systeme mit konzentrierten (DSKP) und verteilten Parametern (DSVP). Mathematische Beschreibung der Modelle (DSKP und DSVP) als Objekte paralleler Simulationen haben formale Darstellung der Topologie (technologische Schemen, Grafiken, Strukturen der Automatisierungssysteme, Sekundärstrukturen wegen Annäherungen usw.)
Nach der topologischen Analyse des Objekts werden Matrix-Vektor-Gleichungssysteme generiert, die als Grundlage für sequentielle oder parallele Objektmodellerzeugung sind. Generiertes System soll durch gewähltes numerisches Verfahren gelöst werden. Diese Verfahren muss Entwickler des Modelles auswählen. Programme, die numerische Verfahren realisieren, bilden Subsystem von Gleichungslösern.
Nach [6,7] folgt, dass ein Subsystem von Gleichungslösern wie ein Teil von Modellierungs-Software der verteilten parallelen Simulationsumgebung ist (SW VPSU) (Abb. 1).
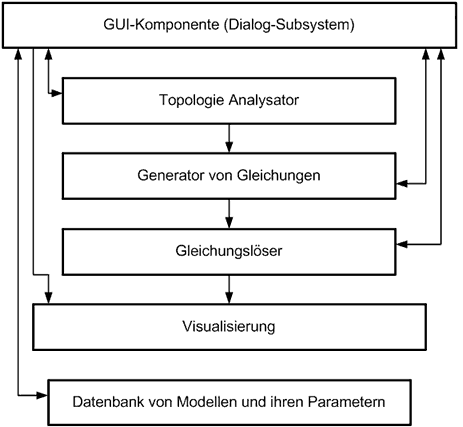
Abbildung 1 – Struktur von VPSU
Aus Abb.1 kann man sehen, dass das Subsystem von Gleichungslösern eng mit dem Gleichungsgenerator-Subsystem gekoppelt ist. Als Eingabeparameter soll Gleichungslöser ein System von Gleichungen in verständlicher für Simulationstools Form (Simulation Model) erhalten. Er soll auch für dieses System die Algorithmen und Software-Lösungen (parallele und sequentielle) entwickeln.
Gleichungslöser stellt ein Programm vor, das den Algorithmus von paralleler numerischer Lösung des Matrix-Vektor-Modells vom Objekt implementiert.
Struktur des Gleichungslösers [7] kann man auf Abb.2 sehen.
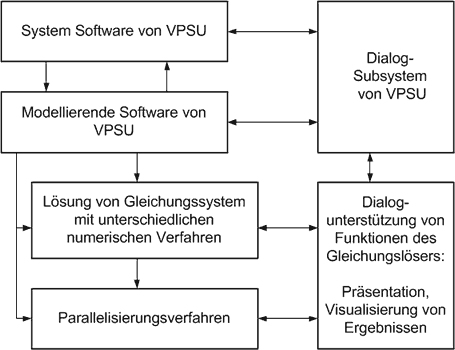
Abbildung 2 – Struktur des Gleichungslösers
Entwicklung des Gleichungslösers besteht aus solchen Etappen.
- Das Zeichnen eines Flussdiagramms konsequenter Lösung des Simulationsmodells, in welchen Berechnungsblöcken der Systemkomponenten sich detaillieren. Anstellung der Reihenfolge für die Berechnung der Variable (abhängig von dynamischen Prozessen).
- Vorschlag und Analyse der möglichen Ansätze zur Parallelisierung. Zeichnen des Flussdiagramms von parallelen Algorithmen zur Lösung des Simulationsmodell, in dem die Blöcke, die parallel berechnet werden, und Informationsaustauschen zwischen parallelen Einheiten detailliert werden.
- Die Implementierung von parallelen und sequentiellen Algorithmen.
- Die Rentabilitätsanalyse, Auswahl des besten parallelen Lösers.
Alle Ansätze zur Parallelisierung kann man in 4 Stufen (Granulationsebene der Prozesse) teilen (Abb. 3).
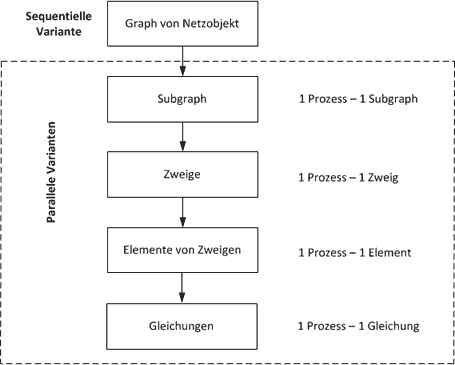
Abbildung 3 – Ansätze zur Parallelisierung
Gleichungslöser soll die beste Variante der Parallelisierung finden, weil von der Auswahl der Parallelisierungsmethode die Geschwindigkeit der Lösung von konkretem Simulationsmodell abhängt.
Funktionen des Subsystems von Gleichungslösern
Aus der Analyse der Struktur von VPSU und Gleichungslöser kann man solche wesentliche Funktionen des Subsystems nennen.
- Die Kommunikation zwischen Subsystemen von topologischer Analyse und Gleichungsgenerator. Die Einführung von diskreten virtuellen parallelen Simulationsmodellen, die schon zur Implementierung bereit sind.
- Die Lösung der Systeme von algebraischen, gewöhnlichen Differentialgleichungen und Gleichungen in partiellen Ableitungen mit Hilfe von parallelen numerischen Verfahren, die in DSKP- und DSVP-Bibliotheken zusammengestellt sind.
- Die Analyse von Konvergenz und Nachhaltigkeit der Lösungen. die Optimierung der Parameter, die sich ändern können.
- Bewertung und Optimierung von Effektivität-Metriken paralleler Lösungen im Vergleich mit sequentiellen Methoden.
- Formierung der Lösungsergebnisse für Visualisierung.
Es ist zu akzeptieren, dass Algorithmen vom Gleichungslöser nicht nur parallele Variante, sondern auch sequentielle Variante unterstützen sollen, weil Hauptprinzip so ist, dass eine Vererbung zwischen alten (sequentiellen) und neuen (parallelen) Modellen sein muss.
Zusammenfassung
Bei der Analyse von Materialien rund um das Thema der Master-Arbeit wurde es festgestellt, dass die Frage der Entwicklung paralleler Gleichungslöser für verteilte parallele Simulationsumgebung und Fragen der Modellierung sehr aktuell heute sind.
Es gibt große Menge von wissenschaftlichen Arbeiten, die nicht nur von Studenten und Aspiranten in DonNTU gemacht sind, sondern auch von ausländischen Autoren. Es gibt wissenschaftliche Zusammenarbeit zwischen FRTI und ausländischen Partnern (Universität Stuttgart, Erlangen, Max-Plank Institut (Magdeburg)), staatlichen Unternehmen („Azot“, Sewerodonezk) und Steinkohlenunternehmen.
Es war Hauptkonzeption von VPSU beschrieben, die Definition des Subsystems von Gleichungslösern war gegeben. Auch waren Etappen der Projektierung des parallelen Gleichungslösers definiert, Funktionen und Eigenschaften des Subsystems wurden festgestellt.
Im Gesamtergebnis, kann man sagen, dass Thema der Master-Arbeit aktuell und nützlich ist. Von Erfüllung der Arbeitsaufgaben sollte sowohl wissenschaftliche Gesellschaft als auch Industrie profitieren.
Literaturverzeichnis
- Абрамов Ф.А., Фельдман Л.П., Святный В.А. Моделирование динамических процессов рудничное Аэрология.- К.: Наук. Мысль, 1981.-284с.
- Святный В.А. Моделирование аэрогазодинамических процессов и разработка систем управления проветривание систем шахт. Докт. дисс, Донецк, ДПИ, 1986
- W. Group, E. Lusk, A. Skjellum Using MPI. Portable Parallel Programming with the Message-Passing Interface. - The MIT Press, Cambridge, Massachusetts, London, England: 1995. - 303с.
- Ахмеров г.г, Численные методы решения обыкновенных дифференциальных уравнений
- Svjatnyj V., Moldovanova O., Smagin A., Resch M., Keller R.: Rabenseifner R. Virtuelle Simulationsmodelle und ein Devirtualisierungsvorgang für die Entwicklung der parallelen Simulatoren von komplexen dynamischen Systemen / 19. Symposium ASIM 2006, Tagungsband, 2006, S. 416 - 421.
- Святный В.А. Проблемы параллельного моделирования сложных динамических систем. Научные труды ДонГТУ, Серия «икота», вып. 6, 1999
- Молдованова О.В. Магистерская работа, ДонГТУ, Донецк, 2000
- Svjatnyj V., Beljaev O., Lapko V., Tschepzov O., Hohmann R.: Zur Entwicklungsorganisation des Simulations-und Servicezentrums für die Kohleindustrie. In: F. Hülsemann u.a. (Hrsg.), Tagungsband 18. ASIM-Symposium Simulationstechnik, Erlangen 2005, SCS 2005, 554-559
- L. P. Feldmann, V. A. Svjatnyj, M. Resch, M. Zeitz: Forschungsgebiet: parallele Simulationstechnik. Научные труды ДонНТУ, 2008.
