Abstract

1 Introduction

2 Problem statement

3 Review of existing methods of visualization of reliefs

   3.1 Irregular network of triangles

   3.2 Technology with limited adaptability

   3.3 Hierarchical triangulation based on the square tree and binary tree of triangles

   3.4 Clustered triangulation

4 Conclusions. Goals and objectives for further research

5 References

1 Introduction

In complex systems, highly realistic virtual reality one of the problems of synthesis of the visual environment is to generate images of terrain.

Technology for synthesizing images of landscapes and relief are needed in many areas of human activity, since the scope of imaging techniques is very wide. Main applications:
1) Submission of topographic data in geographical information systems.
2) Simulators (aircraft, ground-based road transport, trains), which include terrain modeling.
3) Programs for the design of landscape design and construction.
4) Various Computer and video games related to visualization of the reliefs.
5) Systems of the virtual expanded reality.

Consequently, methods of synthesis of realistic images of landscapes and relief are very topical at the moment and will be further developed and improved by the emergence of high-performance GPU and the latest technologies such as CUDA (NVidia) and FireStream (ATI), allowing to make calculations on the GPU for general purposes.

2 Problem Statement

This work will focus on polygon rendering techniques, building the polygonal approximation of the modeled objects in a homogeneous space and expecting lighting, shading and other properties nongeometric on the basis of approximation.

From a geometric point of view, the relief can be represented as three-dimensional surface of general type. The most natural way to specify such a surface is two-dimensional vector function: 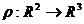, which can be given parametrically: .

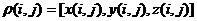The most natural vector formats are TINs, piecewise-linear approximating the simulated terrain 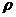network of triangles. Bitmaps, which are two-dimensional grid functions with regularly spaced, typically shows a map of the heights of , such that , where W and H - the width and height of the elevation map, respectively [8]. The last presentation in this paper, we selected the basic input format.

The main task is to construct a reasonably accurate polygonal approximation of the input data that satisfy certain criteria of approximation, a homogeneous space and its subsequent visualization. There are two classes of criteria: view-depended (VD) and view-independed (VI). Errors made by the algorithm for constructing approximations are evaluated step by step, and the total error of the algorithm is considered as the average error, either as the maximum error. When imaging is typically not seen the whole model, but only a part limited four-dimensional cube whose projection on the original three-dimensional space represented by the so-called truncated pyramid of sight.

To perform the tasks required visualization frame rate in the range 50-100 FPS (frames per seconds). One of the important factors in the synthesis of relief and landscapes is the performance of the equipment. Modern graphics systems on a PC can provide rendering performance at the level of 108 triangles per second. Therefore, to increase performance of visualization techniques to most effectively use the GPU for most calculations.

Thus, the problem of synthesizing realistic images of relief and landscapes can be represented as follows:
1. In the world coordinate system is defined height map with a regular step;
2. Necessary to build accurate polygonal approximation of the height field;
3. Visualization of results (Fig. 1), polygonal approximation, taking into account the effects of lighting and shading.

3 Review of existing methods of visualization of reliefs

Direct solution, ie visualization of polygonal mesh terrain elevation map is implicitly defined, hardware and software of the target platform, not a solution to the problem at least for two reasons:
1) it is impossible to achieve interactivity on the target hardware platform due to lack of computing power to render the required number of triangles;
2) an increase in the size of an elevation map proportionally reduced speed construction of the frame

These requirements make it necessary to construct a simplified polygonal model. Such simplification is possible due to:
- Discarding polygons that are not involved in the VF (VF-clipping, VFC);
- Discarding polygons that completely covered by other polygons that are closer to the observer;
- Representation of certain sections of topography with less detail, the simplified polygonal models are called levels of detail (LOD).

Task polygonal network can be constructed from the composition of individual triangles and connected families of triangles, called patches or patches that are more effective approach. Typical data structures with the use of which may be implemented to construct LOD:
- A network of triangles with ancillary information in the form of a tree or other data structures;
- Set monospaced patches placed mosaic manner;
- Wood, typically a binary tree of triangles or squares square tree containing the nodes triangles or patches (patches);
- A set of concentric symmetrical tessellated figures, typically circles or squares cut out the center.

3.1 Irregular network of triangles

The most generalized LOD-algorithms can be regarded as approximations algorithms, expressed in terms of the TIN, ie Reducing the input TIN by reducing the number of triangles contained in it on the basis of certain criteria, which are typically expressed in the requirements on the number of triangles in the target or TIN in the value of the maximum permissible error of approximation.

Fundamentally, the algorithms simplification of polygonal models can be divided into 3 sub-classes:
1) decimation vertex [9];
2) clustering vertex [10];
3) iterative removal of edges.

3.2 Technology with limited adaptability

The method of tile blocks (Fig. 2) using multiple representations of parts of the relief, typically square blocks, processed and stored in advance. At the time of imaging, on the basis of VD-parameters of the stored units collected by the relevant approximation. Since different parts of the terrain can be visualized using blocks of various structures on their boundaries can be formed discontinuities [8].

Technique of geometric mipmapping (GeoMipmaps) [1] generalizes this approach by using an analogy with the texture mipmapping. For each square block of pre-established chain of levels of detail (blocks 17x17), geometric data are redistributed for effective RT-visualization. Selecting the level of detail is rendered on the basis of the distance to the observer and the pre-calculated estimate error screen. Discontinuities on block boundaries are removed dynamically adjusted index of vertices on the boundary of the block with greater detail, providing an exception peaks, causing ruptures.

Geometric maps clipping (Geometry Clipmaps Fig. 3) [2] - contemporary approach to the visualization allows you to transfer a substantial part of the process of constructing LOD of hardware blocks video. VD-approximation of the rendered terrain cached in LVM as mipmaps-pyramid, each level of which is land elevation map covering a 2-fold greater area. In the process of movement of the camera, the levels of the pyramid are shifted, and missing data are incrementally loaded into LVM

3.3 Hierarchical triangulation based on the square tree and binary tree of triangles

The main idea of the described algorithms to create a hierarchy of semiregular nets LOD through iterative detail or coarsening of basic geometric models. Detailing is an iterative bisection base of an isosceles right triangle, generating two similar triangle of smaller size. When roughening used the reverse process - a pair of right-angled triangles iteratively merged.

Work [3] introduced a representation of relief with the use of spatial partitioning based quad-tree, each level is represented by a regular grid with a fixed number of nodes. Root of the tree defines all the workable height map, each level represents one quarter of the area the previous level. In the process of visualization is bypassing quad-tree, during which decisions about using the required level to visualize the site of the approximated surface. In order to eliminate discontinuities at the boundaries of blocks used vertical polygons (walls).

Some works are based on the introduction of additional restrictions and regulations that control the iterative partitioning. Partition quad-tree limited so that the hierarchical levels of tree leaves, represent adjacent areas should not vary by more than one. Such partitions are called limited quad-tree triangulation (RQT, Fig. 4).

Classical algorithm that uses a hierarchical triangulation based on a binary tree of triangles, is ROAM [4]. It is based on a binary tree of triangles, which is a special case of the iterative bisection base of the triangle on the base top. During the operation detail, a pair of triangles divided by a common base peak, located on the adjacent grounds (Fig. 5).

ROAM triangulation algorithm is based on maintaining two priority queues - queues and queue partitions associations. At the time of visualization of these bursts sampled and supported by a binary tree update is suitable, that makes effective use of inter-frame coherence of the processed data and update the final band of triangles incrementally. Priorities for the partitions and associations based on the estimate of the error, defined on the set of triangles.

3.4 Clustered triangulation

Due to the increasing power of the GPU and the constant increase in data to be processed, it is necessary to apply new algorithms relief, allowing to use all the power of GPU. Requested several modern techniques that reduce the average time of processing primitives, with their compositions in the pre-clusters (patches), organized for efficient visualization. The main feature of these approaches is the use of so-called cluster triangulation (Fig. 6), dislodging the primitive unit for constructing LOD of vertices or triangles to the block represents a contiguous portion of the relief.

Algorithm RUSTIC [5] is an extension of ROAM, under which it is proposed to use pre-prepared binary subtrees triangles. CABTT [6] uses a similar idea of caching subtrees of the ROAM, created as needed. Clusters of triangles that are dynamically generated based on the triangulation of the above subtrees can be cached in LVM as vertex arrays, organized in strips of triangles. Chunked LOD [7] - an algorithm that satisfies the task fully. When organizing a parallel streaming of data from persistent storage to meet the requirement for hard real-time visualization of terrain practically unlimited size.

4 Conclusions. Goals and objectives for further research

In the course of the study analyzed the existing problems have been solving this problem. From the perspective of the task, the highest efficiency when rendering static topography show algorithms that use hierarchical triangulation based on the square tree and binary tree of triangles, and their further optimization algorithms cluster triangulations.

The main objectives of this study will be:
1) a detailed analysis of algorithms for synthesizing realistic images of relief and landscapes and their characteristics;
2) study the feasibility of the most effective (realistic) synthesis algorithms on parallel architectures, computer systems, including the architecture of modern GPU graphics card PC, and evaluation of its effectiveness;
3) creation of a prototype software model of the synthesis of realistic images of landscapes and relief using parallel GPU architectures and analysis of the synthesis process in comparison with "classic" solution of the problem.

5 REFERENCES

1. Willem H. de Boer: Fast Terrain Rendering Using Geometrical MipMapping, E mersion Project, October 2000.
2. Losasso F. and Hoppe H. Geometry clipmaps: terrain rendering using nested regular grids. ACM Trans. Graph., 23(3):769–776, 2004.
3. Lindstrom, P., Koller, D., Hodges, L.F., Ribarsky, W., Faust, N., Turner, G.: Level-of-detail management for real-time rendering of phototextured terrain. Tech. rep., Graphics, Visualization, and Usability Center, Georgia Tech (1995). TR 95-06
4. Duchaineau, M., Wolinsky, M., Sigeti, D.E., Miller, M.C., Aldrich, C., Mineev-Weinstein, M.B.: ROAMing terrain: Realtime optimally adapting meshes. In: Proceedings IEEE Visualization, pp. 81–88 (1997)
5. Pomeranz, A.A.: ROAMusing surface triangle clusters (RUSTiC). Master’s thesis, University of California at Davis (2000)
6. Levenberg, J.: Fast view-dependent level-of-detail rendering using cached geometry. In: Proceedings IEEE Visualization, pp. 259– 266. Computer Society Press (2002)
7. Ulrich, T.: Rendering massive terrains using chunked level of detail. In: Super-size-it! Scaling up toMassive VirtualWorlds (ACM SIGGRAPH Tutorial Notes). ACM SIGGRAPH (2000)
8. Визуализация рельефа в реальном времени [Электронный ресурс]. - Режим доступа: http://www.mutpu4.com/docs/terrain-rendering-overview
9. William J. Schroeder, Jonathan A. Zarge, and William E. Lorensen.: Decimation of triangle meshes. Computer Graphics (SIGGRAPH ’92 Proc.), 26(2):65–70, July 1992.
10. Jarek Rossignac and Paul Borrel. Multi-resolution 3D approximations for rendering complex scenes. In B. Falcidieno and T. Kunii, editors, Modeling in Computer Graphics: Methods and Applications, pages 455–465, 1993.

Important note

Master's thesis is not completed yet, while writing this author's abstract. Final Completion: December 2011 Full text of the work and materials on the subject can be obtained from the author or his manager after that date.