Реферат по теме выпускной работы

1 Введение

2 Постановка задачи

3 Обзор существующих методов визуализации рельефов

   3.1 Иррегулярные сети треугольников

   3.2 Техники с ограниченной адаптивностью

   3.3 Иерархическая триангуляция на основе квадродеревьев и бинарных деревьев треугольников

   3.4 Кластерные триангуляции

4 Выводы. Цели и задачи дальнейшего исследования

5 Литература

1 Введение

В сложных системах виртуальной реальности одной из задач синтеза визуальной обстановки является генерация изображений рельефов местности.

Технологии синтеза изображений рельефов и ландшафтов необходимы во многих сферах человеческой деятельности, так как область применения техник визуализации очень широка. Основные области применения:
1) Представление топографических данных в географических информационных системах.
2) Тренажеры-симуляторы (авиационные, наземного автомобильного транспорта, поездов), которые включают в себя моделирование рельефа.
3) Программы для проектирования ландшафтного дизайна и строительства.
4) Различные компьютерные и видео игры, связанные с визуализацией рельефов.
5) Системы виртуальной расширенной реальности.

В связи со сложностью методов синтеза реалистичных изображений рельефов и ландшафтов становится актуальной задача их параллельного решения на существующих параллельных вычислительных системах, а также их решения на появивишихся и широкоиспользуемых в последнее время параллельных вычислительных системах на базе GPU с применением технологий CUDA (NVidia) и FireStream (ATI).

Научная новизна работы - исследование возможности реализации синтеза изображений рельефов и ландшафтов на параллельных вычислительных системах общего назначения GPU с использованием технологии CUDA, а также получение качественных (количество полигонов, ошибка аппроксимации сцены) и временных характеристик (время загрузки карты высот в память, скорость смены кадров) синтеза в сравнении с "классическим методом" решения задачи синтеза изображений рельефов. Планируется получение повышения качества построенных моделей рельефов и уменьшение временных характеристик.

2 Постановка задачи

Данная работа будет фокусироваться на полигональных техниках визуализации, строящих полигональную аппроксимацию моделируемых объектов в однородном пространстве и рассчитывающих освещение, затенение и другие энергетические свойства повершинно либо пофрагментно на основе аппроксимации.

С геометрической точки зрения, рельеф может быть представлен как трехмерная поверхность общего вида. Наиболее естественным способом задания такой поверхности является двумерная векторная функция 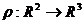, которую можно задать параметрически: .

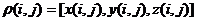Наиболее естественным векторным форматом являются TINs, кусочно-линейно аппроксимирующие моделируемый рельеф 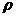сетью треугольников. Растровые форматы, являющиеся двумерными сеточными функциями с регулярным шагом, типично представлены картами высот , такой что , где W и H – ширина и высота карты высот соответственно [8]. Последнее представление в данной работе выбрано основным входным форматом.

Основной задачей является построение достаточно точной полигональной аппроксимации входных данных, удовлетворяющим некоторым критериям аппроксимации, в однородном пространстве и последующая ее визуализация. Выделяют два класса критериев: видозависимые (VD) и видонезависимые (VI). Ошибки, внесенные алгоритмом построения аппроксимаций оцениваются пошагово, и общая ошибка алгоритма рассматривается как средняя ошибка, либо как максимальная ошибка. При визуализации типично рассматривается не вся модель, а только ее часть, ограниченная четырехмерным кубом, проекция которого на изначальное трехмерное пространство представлена так называемой усеченной пирамидой видимости.

Для выполнения задач визуализации необходима скорость смены кадров в пределах 50-100 FPS (frames per seconds). Одним из немаловажных факторов при синтезе рельефов и ландшафтов является производительность аппаратуры. Современные графические системы на базе ПК могут обеспечить производительность визуализации на уровне 108 треугольников в секунду. Следовательно, для увеличения производительности методов визуализации необходимо максимально эффективно применять GPU для большинства вычислений.

Таким образом, задачу синтеза реалистических изображений рельефов и ландшафтов можно представить следующим образом:
1. В мировой системе координат задана карта высот с регулярным шагом;
2. Необходимо построение точной полигональной аппроксимации по карте высот;
3. Визуализация результатов (рис. 1) полигональной аппроксимации с учетом эффектов освещения и затенения.

3 Обзор существующих методов визуализации рельефов

Прямое решение, т.е. визуализация полигональной сетки рельефа, неявно заданной картой высот, аппаратно-программными средствами целевой платформы, не является решением поставленной задачи как минимум по двум причинам:
1) невозможно достичь интерактивности на целевой аппаратной платформе ввиду недостатка вычислительной мощности для визуализации необходимого количества треугольников;
2) при увеличении размеров карты высот, пропорционально уменьшается скорость построения кадра.

Эти требования приводят к необходимости построения упрощенной полигональной модели. Такое упрощение возможно за счет:
- отбрасывания полигонов, не попадающих в VF (VF-отсечение, VFC);
- отбрасывания полигонов, полностью перекрытых другими полигонами, находящимися ближе к наблюдателю;
- представления некоторых участков рельефа с меньшей детализацией, упрощенные полигональные модели получили название уровней детализации (LOD).

Целевая полигональная сеть может быть построена из композиции как отдельных треугольников, так и связных семейств треугольников, называемых заплатками или патчами, что является более эффективным подходом. Типичные структуры данных, с использованием которых может быть реализовано построение LOD:
- сеть треугольников со вспомогательной информацией в виде дерева либо другой структуры данных;
- множеств одноразмерных заплаток, размещенных мозаичным способом;
- дерево, типично бинарное дерево треугольников или квадродерево квадратов, содержащее в узлах треугольники или заплатки (патчи);
- множество концентрических симметричных тесселированных фигур, типично окружностей или квадратов с вырезанным центром.

3.1 Иррегулярные сети треугольников

Наиболее обобщенными LOD-алгоритмами можно считать алгоритмы построения аппроксимаций, выраженные в терминах TIN, т.е. редуцирующие входную TIN путем сокращения количества содержащихся в ней треугольников на основании некоторых критериев, которые типично выражены в требованиях на количество треугольников в целевой TIN либо в значении максимально допустимой ошибки аппроксимации.

Принципиально, алгоритмы упрощения полигональных моделей можно разделить на 3 подкласса:
1) прореживание вершин [9]. Агоритм, суть которого заключается в итеративном выборе вершины для исключения, удаления всех прилегающих граней и ретриангуляции образовавшихся “пустот”.
2) кластеризация вершин [10]. Алгоритм ориентирован на обработку произвольных полигональных входных данных. Вокруг обрабатываемой модели описывается ограничивающий объем, регулярно тесселируемый на прямоугольные параллелепипеды (клетки). Вершины, находящиеся в пределах одной клетки, объединяются, и грани модели обновляются соответствующим образом. Описанный процесс может быть эффективно реализован, однако он может внести в модель очень значительные топологические изменения.
3) итеративное удаление граней. Основной проблемой данного подхода типично считается то, что построенный на нем процесс симплификации не может объединять несвязные области, однако это редко является проблемой при RT-визуализации рельефа. Существенная разница между этими алгоритмами заключается в стратегии выбора очередной грани, подлежащей удалению.

3.2 Техники с ограниченной адаптивностью

Метод тайловых блоков (рис. 2) использует множественные представления частей рельефа, типично квадратные блоки, обработанные и сохраненные предварительно. В момент визуализации, на основании VD-параметров, из сохраненных блоков собирается соответствующая аппроксимация. Поскольку различные участки рельефа могут быть визуализированы с использованием блоков различной структуры, на их границах могут образовываться разрывы [8].

Техника геометрического мипмаппинга (GeoMipmaps) [1] обобщает этот подход, используя аналогию с текстурным мипмаппингом. Для каждого квадратного блока предварительно создается цепочка уровней детализации (блоки 17x17), геометрические данные которых перераспределяются для эффективной RT-визуализации. Выбор визуализируемого уровня детализации делается на основе расстояния до наблюдателя и предварительно рассчитанной оценки экранной ошибки. Разрывы на границах блоков устраняются динамической коррекцией индексирования вершин, расположенных на границе блока с большей детализацией, обеспечивающей исключение вершин, вызывающих разрывы.

Геометрические карты отсечения (Geometry Clipmaps рис.3) [2]– современный подход в визуализации, позволяет перенести существенную часть процесса построения LOD на аппаратные блоки видеоадаптера. VD-аппроксимация визуализируемого ландшафта кешируется в LVM как мипмап-пирамида, каждый следующий уровень которой представляет участок карты высот, охватывающий в 2 раза большую площадь. В процессе передвижения камеры, уровни пирамиды сдвигаются, а недостающие данные инкрементно загружаются в LVM.

3.3 Иерархическая триангуляция на основе квадродеревьев и бинарных деревьев треугольников

Основная идея описываемых алгоритмов в создании иерархии полурегулярных сеток LOD посредством итеративных детализации или огрубления базовых геометрических моделей. Детализация заключается в итеративной бисекции основания равнобедренного прямоугольного треугольника, порождающей два подобных треугольника меньших размеров. При огрублении используется обратный процесс – пары прямоугольных треугольников итеративно объединяются.

Работа [3] вводит представление рельефа с использованием пространственного разбиения на основе квадродерева, каждый уровень которого представлен регулярной сеткой с фиксированным числом узлов. Корень дерева задает всю обрабатываемую карту высот, каждый следующий уровень представляет одну четверть от площади предыдущего уровня. В процессе визуализации производится обход квадродерева, в ходе которого принимаются решения об использовании необходимого уровня для визуализации участка аппроксимируемой поверхности. Для устранения разрывов на границах блоков используются вертикальные многоугольники (стенки).

Некоторые работы основаны на введении дополнительных ограничений и правил, контролирующих итеративные разбиения. Разбиение квадродерева ограничивалось таким образом, что иерархические уровни листьев дерева, представляющих соседние области, не должны различаться более чем на один. Такие разбиения получили название ограниченные квадродеревья триангуляции (RQT, рис. 4).

Классическим алгоритмом, использующим иерархическую триангуляцию на основе бинарных деревьев треугольников, является ROAM [4]. Он основан на бинарном дереве треугольников, которое является специальным случаем итеративной бисекции основания треугольника по базовой вершине. В процессе операции детализации, пара треугольников разбивается по общей базовой вершине, находящейся на смежных основаниях (рис. 5).

Алгоритм триангуляции ROAM основан на поддержании двух очередей с приоритетами – очереди разбиений и очереди объединений. В момент визуализации из этих очередей производится выборка и поддерживаемое бинарное дерево обновляется соответствующе, что позволяет эффективно использовать межкадровую когерентность обрабатываемых данных и обновлять конечные полосы треугольников инкрементально. Приоритеты разбиений и объединений основаны на оценке ошибки, определенной на множестве треугольников.

3.4 Кластерные триангуляции

В связи с увеличением мощности GPU и постоянным увеличением обрабатываемых данных, необходимо применять новые алгоритмы построения рельефов, позволяющих использовать всю мощность GPU. Предложено несколько современных техник, уменьшающих среднее время обработки примитивов, с помощью предварительной их композиции в кластеры (патчи), организованные для эффективной визуализации. Основной чертой этих подходов является использование так называемой кластерной триангуляции (рис. 6), смещающий примитивную единицу построения LOD от вершин или треугольников до блоков, представляющих непрерывную часть рельефа.

Алгоритм RUSTIC [5] является расширением ROAM, в рамках которого предлагается использовать заранее подготовленные бинарные поддеревья треугольников. CABTT [6] использует похожую идею кеширования поддеревьев ROAM, создаваемых по мере необходимости. Кластеры треугольников, динамически формируемые на основании триангуляции вышеописанных поддеревьев, могут быть закешированы в LVM как вершинные массивы, организованные в полосы треугольников. Chunked LOD [7] – алгоритм, который удовлетворяет поставленной задаче в полной мере. При организации параллельной потоковой загрузки данных с постоянного носителя, обеспечивается выполнение требований жесткого реального времени при визуализации рельефа практически не ограниченного размера.

4 Выводы. Цели и задачи дальнейшего исследования

В ходе проведения исследования проблемы были проанализированы существующие решения поставленной задачи. С точки зрения задачи синтеза изображений рельефов и ландшафтов, наибольшую эффективность при визуализации статического рельефа показали алгоритмы, использующие иерархическую триангуляцию на основе квадродеревьев и бинарных деревьев треугольников, а также их дальнейшая оптимизация в алгоритмы кластерных триангуляций.

Главными задачами данной работы будут являться:
1) детальный анализ алгоритмов синтеза реалистических изображений рельефов и ландшафтов и их характеристик;
2) исследование возможности реализации наиболее эффективных алгоритмов синтеза на параллельных архитектурах вычислительных систем, включая архитектуры GPU современных видеокарт ПК, и оценка ее эффективности;
3) создание прототипа программной модели синтеза реалистических изображений рельефов и ландшафтов с использованием параллельных архитектур GPU и анализ характеристик процесса синтеза в сравнении с «классическим» решением задачи.

5 Литература

1. Willem H. de Boer: Fast Terrain Rendering Using Geometrical MipMapping, E mersion Project, October 2000.
2. Losasso F. and Hoppe H. Geometry clipmaps: terrain rendering using nested regular grids. ACM Trans. Graph., 23(3):769–776, 2004.
3. Lindstrom, P., Koller, D., Hodges, L.F., Ribarsky, W., Faust, N., Turner, G.: Level-of-detail management for real-time rendering of phototextured terrain. Tech. rep., Graphics, Visualization, and Usability Center, Georgia Tech (1995). TR 95-06
4. Duchaineau, M., Wolinsky, M., Sigeti, D.E., Miller, M.C., Aldrich, C., Mineev-Weinstein, M.B.: ROAMing terrain: Realtime optimally adapting meshes. In: Proceedings IEEE Visualization, pp. 81–88 (1997)
5. Pomeranz, A.A.: ROAMusing surface triangle clusters (RUSTiC). Master’s thesis, University of California at Davis (2000)
6. Levenberg, J.: Fast view-dependent level-of-detail rendering using cached geometry. In: Proceedings IEEE Visualization, pp. 259– 266. Computer Society Press (2002)
7. Ulrich, T.: Rendering massive terrains using chunked level of detail. In: Super-size-it! Scaling up toMassive VirtualWorlds (ACM SIGGRAPH Tutorial Notes). ACM SIGGRAPH (2000)
8. Визуализация рельефа в реальном времени [Электронный ресурс]. - Режим доступа: http://www.mutpu4.com/docs/terrain-rendering-overview
9. William J. Schroeder, Jonathan A. Zarge, and William E. Lorensen.: Decimation of triangle meshes. Computer Graphics (SIGGRAPH ’92 Proc.), 26(2):65–70, July 1992.
10. Jarek Rossignac and Paul Borrel. Multi-resolution 3D approximations for rendering complex scenes. In B. Falcidieno and T. Kunii, editors, Modeling in Computer Graphics: Methods and Applications, pages 455–465, 1993.

Важное замечание

При написании данного автореферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2011 г. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.