Реферат з теми випускної роботи

1 Введення

2 Постановка завдання

3 Огляд існуючих методів візуалізації рельєфів

   3.1 Іррегулярні мережі трикутників

   3.2 Методи з обмеженою адаптивністю

   3.3 Ієрархічна тріангуляція на основі квадродерев і бінарних дерев трикутників

   3.4 Кластерні тріангуляції

4 Виводи. Цілі і завдання подальшого дослідження

5 Література

1 Введення

У складних високо реалістичних системах віртуальної реальності одним із завдань синтезу візуальної обстановки є генерація зображень рельєфів місцевості.

Технології синтезу зображень рельєфів і ландшафтів необхідні в багатьох сферах людської діяльності, оскільки область застосування техніки візуалізації дуже різноманітна. Основні області застосування:
1) Представлення топографічних даних в географічних інформаційних системах.
2) Тренажери-симулятори (авіаційні, наземного автомобільного транспорту, потягів), які включають моделювання рельєфу.
3) Програми для проектування ландшафтного дизайну та будівництва.
4) Різні комп'ютерні і відео ігри, пов'язані з візуалізацією рельєфів.
5) Системи віртуальної розширеної реальності.

У зв'язку зі складністю методів синтезу реалістичних зображень рельєфів і ландшафтів стає актуальним завдання їх паралельного вирішення на існуючих паралельних обчислювальних системах, а також їх вирішення на з’явившихся та загально використовуваємих останнім часом паралельних обчислювальних системах на базі GPU із застосуванням технологій CUDA (Nvidia) і Firestream (ATI).

Наукова новизна роботи - дослідження можливості реалізації синтезу зображень рельєфів і ландшафтів на паралельних обчислювальних системах загального призначення GPU з використанням технології CUDA, а також отримання якісних характеристик (кількість полігонів, помилка апроксимації сцени) і характеристик часу (час завантаження карти висот в пам'ять, швидкість зміни кадрів) синтезу порівняно з "класичним методом" рішення задачі синтезу зображень рельєфів. Планується отримання підвищення якості побудованих моделей рельєфів і зменшення характеристик часу.

2 Постановка завдання

Ця робота фокусуватиметься на полігональній техніці візуалізації, що будує полігональну апроксимацію модельованих об'єктів в однорідному просторі і розраховує освітлення, затінювання та інші енергетичні властивості повершинно або пофрагментно на основі апроксимації.

З геометричної точки зору, рельєф може бути представлений як тривимірна поверхня загального вигляду. Найбільш природним способом завдання такої поверхні є двовимірна векторна функція: 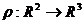, яку можна задати параметрично: .

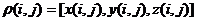Найбільш природним векторним форматом є TINs, що кусочно-лінійно апроксимують модельований рельєф 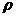мережею трикутників. Растрові формати, що є двовимірними сітковими функціями з регулярним кроком, типово представлені картами висот , такими що , де W і H - ширина та висота карти висот відповідно [8]. Останнє уявлення в даній роботі вибране основним вхідним форматом.

Основним завданням є побудова достатньо точної полігональної апроксимації вхідних даних, що задовольняє деяким критеріям апроксимації, в однорідному просторі і подальша її візуалізація. Виділяють два класи критеріїв: видозалежні (VD) та видонезалежні (VI). Помилки, внесені алгоритмом побудови апроксимацій оцінюються покроково, і загальна помилка алгоритму розглядається як середня помилка, або як максимальна помилка. При візуалізації типово розглядається не вся модель, а тільки її частина, обмежена чотиривимірним кубом, проекція якого на початковий тривимірний простір представлена так званою усіченою пірамідою видимості.

Для виконання завдань візуалізації необхідна швидкість зміни кадрів в межах 50-100 FPS (frames per seconds). Одним з важливих чинників при синтезі рельєфів і ландшафтів є продуктивність апаратури. Сучасні графічні системи на базі ПК можуть забезпечити продуктивність візуалізації на рівні 108 трикутників в секунду. Отже, для збільшення продуктивності методів візуалізації необхідно максимально ефективно застосовувати GPU для більшості обчислень.

Отже, завдання синтезу реалістичних зображень рельєфів і ландшафтів можна представити таким чином:
1. У світовій системі координат задана карта висот з регулярним кроком;
2. Необхідна побудова точної полігональної апроксимації по карті висот; 3. Візуалізація результатів (мал. 1) полігональної апроксимації з урахуванням ефектів освітлення і затінювання.

3 Огляд існуючих методів візуалізації рельєфів

Пряме рішення, тобто візуалізація полігональної сітки рельєфу, неявно заданою картою висот, апаратно-програмними засобами цільової платформи, не є рішенням поставленої задачі як мінімум по двох причинах:
1) неможливо досягти інтерактивності на цільовій апаратній платформі, зважаючи на недолік обчислювальної потужності для візуалізації необхідної кількості трикутників;
2) при збільшенні розмірів карти висот, пропорційно зменшується швидкість побудови кадру.

Ці вимоги приводять до необхідності побудови спрощеної полігональної моделі. Таке спрощення можливе за рахунок:
- відкидання полігонів, що не потрапляють в VF (VF-відсічення, VFC);
- відкидання полігонів, повністю перекритих іншими полігонами, що знаходяться ближче до спостерігача;
- представлення деяких ділянок рельєфу з меншою деталізацією, спрощені полігональні моделі отримали назву рівнів деталізації (LOD).

Цільова полігональна мережа може бути побудована з композиції як окремих трикутників, так і зв'язних сімейств трикутників, званих латками або патчами, що є ефективнішим підходом. Типові структури даних, з використанням яких може бути реалізоване побудова LOD:
- мережа трикутників з допоміжною інформацією у вигляді дерева або іншої структури даних;
- безліч однорозмірних латок, розміщених мозаїчним способом;
- дерево, типове бінарне дерево трикутників або квадродерево квадратів, що містить у вузлах трикутники або латки (патчі);
- безліч концентричних симетричних тесселірованних фігур, типово кіл або квадратів з вирізаним центром.

3.1 Іррегулярні мережі трикутників

Найбільш узагальненими LOD-алгоритмами можна вважати алгоритми побудови апроксимацій, виражені в термінах TIN, тобто що редукують вхідну TIN шляхом скорочення кількості трикутників, що містяться в ній, на підставі деяких критеріїв, які типово виражені у вимогах на кількість трикутників в цільовій TIN або в значенні максимально допустимої помилки апроксимації.

Принципово, алгоритми спрощення полігональних моделей можна розділити на 3 підкласи:
1) проріджування вершин [9];
2) кластеризація вершин [10];
3) ітеративне видалення граней.

3.2 Методи з обмеженою адаптивністю

Метод тайлових блоків (мал. 2) використовує множинні представлення частин рельєфу, типово квадратні блоки, оброблені і збережені заздалегідь. У момент візуалізації, на підставі VD-параметрів, із збережених блоків збирається відповідна апроксимація. Оскільки різні ділянки рельєфу можуть бути візуалізовані з використанням блоків різної структури, на їх межах можуть утворюватися розриви [8].

Техніка геометричного міпмаппінга (Geomipmaps) [1] узагальнює цей підхід, використовуючи аналогію з текстурним міпмаппінгом. Для кожного квадратного блоку заздалегідь створюється ланцюжок рівнів деталізації (блоки 17x17), геометричні дані яких перерозподіляються для ефективної RT-візуалізації. Вибір рівня деталізації, що візуалізується, робиться на основі відстані до спостерігача і заздалегідь розрахованої оцінки екранної помилки. Розриви на межах блоків усуваються динамічною корекцією індексування вершин, розташованих на межі блоку з більшою деталізацією, що забезпечує виключення вершин, що викликають розриви.

Геометричні карти відсікання (Geometry Clipmaps мал.3) [2]- сучасний підхід у візуалізації, дозволяє перенести істотну частину процесу побудови LOD на апаратні блоки відеоадаптера. VD-апроксимація ландшафту кешується, що візуалізується, в LVM як міпмап-піраміда, кожен наступний рівень якої представляє ділянка карти висот, що охоплює в 2 рази більшу площу. В процесі пересування камери, рівні піраміди зрушуються, а необхідні дані інкрементно завантажуються в LVM.

3.3 Ієрархічна тріангуляція на основі квадродерев і бінарних дерев трикутників

Основна ідея описуваних алгоритмів в створенні ієрархії напіврегулярних сіток LOD за допомогою ітеративної деталізації або огрублення базових геометричних моделей. Деталізація полягає в ітеративній бісекції основи рівнобедреного прямокутного трикутника, такій, що породжує два подібні трикутники менших розмірів. При огрубленні використовується зворотній процес - пари прямокутних трикутників ітеративно об'єднуються.

Робота [3] вводить представлення рельєфу з використанням просторового розбиття на основі квадродерева, кожен рівень якого представлений регулярною сіткою з фіксованим числом вузлів. Корінь дерева задає всю оброблювану карту висот, кожен наступний рівень представляє одну чверть від площі попереднього рівня. В процесі візуалізації проводиться обхід квадродерева, в ході якого приймаються вирішення про використання необхідного рівня для візуалізації ділянки поверхні, що апроксимується. Для усунення розривів на межах блоків використовуються вертикальні багатокутники (стінки).

Деякі роботи засновані на введенні додаткових обмежень і правил, контролюючих ітеративне розбиття. Розбиття квадродерева обмежувалося таким чином, що ієрархічні рівні листя дерева, що представляє сусідні області, не повинні розрізнятися більш ніж на один. Таке розбиття отримало назву обмежені квадродерева тріангуляції (RQT, мал. 4).

Класичним алгоритмом, що використовує ієрархічну тріангуляцію на основі бінарних дерев трикутників, є ROAM [4]. Він заснований на бінарному дереві трикутників, яке є спеціальним випадком ітеративною бісекції основи трикутника по базовій вершині. В процесі операції деталізації, пара трикутників розбивається по загальній базовій вершині, що знаходиться на суміжних основах (мал. 5).

Алгоритм тріангуляції ROAM заснований на підтримці двох черг з пріоритетами - черги розбиття і черги об'єднань. У момент візуалізації з цих черг проводиться вибірка і підтримуване бінарне дерево оновлюється відповідно, що дозволяє ефективно використовувати міжкадрову когерентність оброблюваних даних і оновлювати кінцеві смуги трикутників інкрементально. Пріоритети розбиття і об'єднань засновані на оцінці помилки, визначеної на безлічі трикутників.

3.4 Кластерні тріангуляції

У зв'язку із збільшенням потужності GPU і постійним збільшенням оброблюваних даних, необхідно застосовувати нові алгоритми побудови рельєфів, що дозволяють використовувати всю потужність GPU. Запропоновано декілька сучасних методів, що зменшують середній час обробки примітивів, за допомогою попередньої їх композиції в кластери (патчі), організовані для ефективної візуалізації. Основною межею цих підходів є використання так званої кластерної тріангуляції (мал. 6), що зміщує примітивну одиницю побудови LOD від вершин або трикутників до блоків, що представляють безперервну частину рельєфу.

Алгоритм RUSTIC [5] є розширенням ROAM, в рамках якого пропонується використовувати заздалегідь підготовлені бінарні піддерева трикутників. CABTT [6] використовує схожу ідею кешування піддерев ROAM, що створюються в міру необхідності. Кластери трикутників, що динамічно формуються на підставі тріангуляції вищеописаних піддерев, можуть бути закешовані в LVM як вершинні масиви, організовані в смуги трикутників. Chunked LOD [7] - алгоритм, який задовольняє поставленому завданню повною мірою. При організації паралельного потокового завантаження даних з постійного носія, забезпечується виконання вимог жорсткого реального часу при візуалізації рельєфу практично не обмеженого розміру.

4 Виводи. Цілі і завдання подальшого дослідження

В ході проведення дослідження проблеми були проаналізовані існуючі рішення поставленої задачі. З погляду завдання синтезу зображень рельєфів та ландшафтів, найбільшу ефективність при візуалізації статичного рельєфу показали алгоритми, що використовують ієрархічну тріангуляцію на основі квадродеревев і бінарних дерев трикутників, а також їх подальша оптимізація в алгоритми кластерних тріангуляцій.

Головними завданнями даної роботи будуть:
1) детальний аналіз алгоритмів синтезу реалістичних зображень рельєфів і ландшафтів і їх характеристик;
2) дослідження можливості реалізації найбільш ефективних (реалістичних) алгоритмів синтезу на паралельній архітектурі обчислювальних систем, включаючи архітектуру GPU сучасних відеокарт ПК, і оцінка її ефективності;
3) створення прототипу програмної моделі синтезу реалістичних зображень рельєфів і ландшафтів з використанням паралельної архітектури GPU і аналіз характеристик процесу синтезу порівняно з «класичним» рішенням завдання.

5 Література

1. Willem H. de Boer: Fast Terrain Rendering Using Geometrical MipMapping, E mersion Project, October 2000.
2. Losasso F. and Hoppe H. Geometry clipmaps: terrain rendering using nested regular grids. ACM Trans. Graph., 23(3):769–776, 2004.
3. Lindstrom, P., Koller, D., Hodges, L.F., Ribarsky, W., Faust, N., Turner, G.: Level-of-detail management for real-time rendering of phototextured terrain. Tech. rep., Graphics, Visualization, and Usability Center, Georgia Tech (1995). TR 95-06
4. Duchaineau, M., Wolinsky, M., Sigeti, D.E., Miller, M.C., Aldrich, C., Mineev-Weinstein, M.B.: ROAMing terrain: Realtime optimally adapting meshes. In: Proceedings IEEE Visualization, pp. 81–88 (1997)
5. Pomeranz, A.A.: ROAMusing surface triangle clusters (RUSTiC). Master’s thesis, University of California at Davis (2000)
6. Levenberg, J.: Fast view-dependent level-of-detail rendering using cached geometry. In: Proceedings IEEE Visualization, pp. 259– 266. Computer Society Press (2002)
7. Ulrich, T.: Rendering massive terrains using chunked level of detail. In: Super-size-it! Scaling up toMassive VirtualWorlds (ACM SIGGRAPH Tutorial Notes). ACM SIGGRAPH (2000)
8. Визуализация рельефа в реальном времени [Электронный ресурс]. - Режим доступа: http://www.mutpu4.com/docs/terrain-rendering-overview
9. William J. Schroeder, Jonathan A. Zarge, and William E. Lorensen.: Decimation of triangle meshes. Computer Graphics (SIGGRAPH ’92 Proc.), 26(2):65–70, July 1992.
10. Jarek Rossignac and Paul Borrel. Multi-resolution 3D approximations for rendering complex scenes. In B. Falcidieno and T. Kunii, editors, Modeling in Computer Graphics: Methods and Applications, pages 455–465, 1993.

Важливе зауваження

При написанні даного автореферату магістерська робота ще не завершена. Остаточне завершення: грудень 2011 р. Повний текст роботи і матеріали по темі можуть бути отримані у автора або його керівника після вказаної дати.