Реферат по теме выпускной работы
- Введение
- Актуальность
- Научная и практическая значимость
- Планируемые практические результаты
- Задача Коши
- Эффективность и масштабируемость параллельных алгоритмов блочного умножения матриц
- Основные показатели параллельных вычислений
- Анализ алгоритмов Кэннона
- Выводы
- Список литературы
Введение
В современном мире одним из основных направлений вычислительной техники являются параллельные вычислительные системы. Это связано с потребностью эффективного решения фундаментальных научных и инженерных задач, которые требуют огромных объемов вычислений, с использованием мощных вычислительных ресурсов.
С ростом вычислительных мощностей вычислительных систем, современных суперкомпьютеров, кластеров рабочих станций стало возможным решение многих задач, которые предполагают выполнение огромных объемов вычислений за приемлемое время. Это достигается путем распараллеливания алгоритмов и использования многопроцессорных систем.
Организация параллельности вычислений, когда в один и тот же момент выполняется одновременно несколько операций обработки данных, осуществляется, в основном, за счет введения избыточности функциональных устройств (многопроцессорности). В этом случае можно достичь ускорения процесса решения вычислительной задачи, если осуществить разделение применяемого алгоритма на информационно независимые части и организовать выполнение каждой части вычислений на разных процессорах. Подобный подход позволяет выполнять необходимые вычисления с меньшими затратами времени, и возможность получения максимально-возможного ускорения ограничивается только числом имеющихся процессоров и количеством "независимых" частей в выполняемых вычислениях [1].
Однако при разработке параллельных алгоритмов численного решения любых сложных динамических задач важным моментом является анализ качества использования параллелизма, состоящий обычно в оценке получаемого ускорения процесса вычислений (сокращения времени решения задачи) [1].
Актуальность
Применение параллельных вычислительных систем является стратегическим направлением развития вычислительной техники. Это обстоятельство вызвано не только принципиальным ограничением максимально возможного быстродействия обычных последовательных ЭВМ, но и практически постоянным наличием вычислительных задач, для решения которых возможностей существующих средств вычислительной техники всегда оказывается недостаточно[1].
Эффективность реализации параллельных вычислений во многом зависит от адекватности отображения вычислительного алгоритма на параллельную архитектуру, согласования свойств алгоритма и особенностей суперкомпьютера, также выполнение параллельного алгоритма не может быть изучено в отрыве от параллельной вычислительной системы, на которой он реализован.
Научная и практическая значимость
Как известно обычные дифференциальные уравнения являются основой современных инженерных задач. Именно поэтому важно исследовать одношаговые методы решения задачи Коши с отображением на многопроцессорной архитектуре и провести анализ масштабируемости параллельных алгоритмов.
Планируемые практические результаты
В процессе работы над дипломной работой планируется проанализировать параллельные одношаговые методы задачи Коши, а именно исследовать масштабируемость методов, построить функцию изоэффективности и проследить зависимость количества процессоров вычислительной системы от размера решаемой задачи.
Задача Коши
Задача Коши для системы обыкновенных дифференциальных уравнений (СОДУ) первого порядка с известными начальными условиями имеет вид (1). Существует много параллельных методов решения задачи Коши для СОДУ первого порядка [8].
Однако все они включают в себя матричное умножение. Поэтому важным этапом является исследование параллельного матричного умножения.
Эффективность и масштабируемость параллельных алгоритмов блочного умножения матриц
Матричное умножение – одна из основных операций, которая выполняется при решении задач и в тоже время оно является достаточно трудоемким с операционной и коммутативной точки зрения. Поэтому эффективность решения этой задачи – важный фактор.
Топология решетка и гиперкуб являются наиболее подходящими для реализации таких операций. Для такой топологии вычисление матричных арифметических операций можно свести к выполнению операций с блоками матриц.
Существует несколько таких алгоритмов. В данной работе рассматривается семейство алгоритмов Кэннона, которое основано на блочном разбиении матриц.
В алгоритме Кэннона две исходные матрицы A и B и матрица результат C разделяются на блоки. Семейства Кэннона изменяет отображения блоков двух из трех матриц, которые берут участие в вычислении произведения.
Пусть количество столбцов/строк матрицы n кратно числу узлов решетки p. Количество узлов решетки по вертикали/горизонтали равно q. Если представить матрицы в виде квадратных блоков размером k=n/q элементов, то каждому узлу можно однозначно поставить в соответствие такой блок.
Основные показатели параллельных вычислений
Рассмотрим общепринятые и наиболее используемые в параллельных вычислениях показатели:
– время последовательного выполнения алгоритма, время,
необходимое для решения задачи заданного размера на одном процессоре с помощью наилучшего последовательного алгоритма; 
– время решения задачи заданного размера с использованием
параллельного алгоритма на параллельном компьютере из p процессоров без учета обменных операций,
собственно, время реализации вычислений на параллельном компьютере;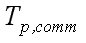
– коммуникационная трудоемкость,
сложность алгоритма или время выполнения межпроцессорных операций обмена при реализации параллельного алгоритма
решения задачи заданного размера;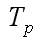
– время параллельного выполнения,
общее время реализации параллельного алгоритма на параллельной архитектуре: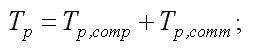
– доля обменных операций к общему времени выполнения параллельного алгоритма: 
– максимальная степень параллелизма, максимальное
количество процессоров, используемых в процессе выполнения параллельного алгоритма;
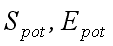– коэффициенты потенциального
ускорения и эффективности (без учета операций обмена); S, E – коэффициенты реального ускорения и эффективности,
параллельного алгоритма (с учетом обменных операций)[2].
Динамические характеристики параллельных алгоритмов зависят от многих переменных, таких как количество процессоров вычислительной системы p и размерности решаемой задачи m.
Также важной характеристикой является ускорение, которая показывает во сколько раз быстрее параллельный алгоритм выполняется на параллельном компьютере из p процессоров по сравнению с последовательным вариантом решения задачи.
Коэффициент ускорения определяется, как отношение времени решения задачи на однопроцессорной вычислительной системе ко времени выполнения параллельного алгоритма. Различают потенциальный и реальный параллелизм, а, следовательно, и соответствующие коэффициенты ускорения. Коэффициент потенциального ускорения учитывает только внутренний, скрытый параллелизм метода решения задачи без учета операций обмена и других накладных расходов:
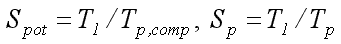
Под масштабируемостью понимается способность параллельной системы к увеличению производительности при увеличении числа процессоров. При фиксированном размер задачи и росте числа процессоров – параллельная эффективность падает. При фиксированном числе процессоров и росте размера задачи – параллельная эффективность растет. Параллельный алгоритм называется масштабируемым, если при увеличении числа процессоров можно увеличивать размерность задачи так, чтобы поддержать параллельную эффективность постоянной.
Следующей важной характеристикой параллельного алгоритма является коэффициент эффективности (efficiency). Эффективность использования параллельным алгоритмом процессоров при решении задачи вычисляется следующим образом:
Коэффициент эффективности определяет среднюю долю времени выполнения алгоритма, в течение которого процессоры реально используются для решения задачи, то есть качество загрузки параллельного оборудования. Существует несколько подходов для количественной оценки свойств масштабируемости алгоритма. Наиболее применяемой является метрика, предложенная и основанная на введении функции равной эффективности или изоэффективности. Изоэффективный анализ – мера масштабируемости параллельных алгоритмов. Для характеристики свойств масштабируемости оценивают накладные расходы (время T0) на организацию взаимодействия процессоров, синхронизацию параллельных вычислений и т.п.:
Функция изоэффективности является одним из таких метрики масштабируемости, которая является мерой алгоритмической способности эффективно использовать большее число процессоров на параллельной архитектуре. Функция изоэффективности сочетания параллельного алгоритма и параллельные архитектуры зависит от размерности задачи и числа процессоров, необходимых для поддержания фиксированной эффективности или достижения ускорения, увеличивающейся пропорционально с ростом числа процессоров [3]. Эффективность параллельной системы считается, как
Анализ алгоритмов Кэннона
Алгоритм вычисления матричного произведения с сохранением отображения блоков матрицы-результата С
Алгоритм включает в себя шаги:блоки строк матрицы A сдвигаются циклично влево на i узлов по горизонтали, где i – индекс строки матрицы A .
блоки столбцов матрицы B сдвигаются циклично вверх на j узлов по вертикали, где j – индекс столбца матрицы B.
Алгоритм выполняется за q шагов, где q – размерность вычислительной решетки. Каждый шаг состоит из следующих действий:
на вычислительном узле решетки с индексами (i,j) производится умножение блоков A(i,j) и B(i,j).
Циклическое смещение блоков матрицы A вправо на 1 узел по горизонтали решетки.
Циклическое смещение блоков матрицы B вверх на 1 узел по вертикали решетки.
Рис.1 – Циклическое смещение блоков
Результат умножения матриц хранится в матрицы C, блоки которой не подлежат смещению.
Анализ эффективности
Время выполнения п.1) или п.2) согласно [1] можно рассчитать по формуле:
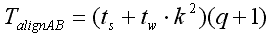
Время умножения матриц в одном блоке:
Время циклического сдвига для п. с) и b):
Суммарное время выполнения алгоритма:
Отсюда получаем ускорение параллельного алгоритма и эффективность использования параллельным алгоритмом процессоров при решении задачи:
Алгоритм вычисления матричного произведения с сохранением отображения блоков матрицы A
Алгоритм включает в себя шаги:блоки строк матрицы B сдвигаются циклично вправо на i узлов по горизонтали, где i – индекс строки матрицы B.
блоки столбцов матрицы B сдвигаются циклично вверх на j узлов по вертикали, где j – индекс столбца матрицы B.
блоки строк матрицы C сдвигаются циклично вправо на i узлов по горизонтали, где i – индекс строки матрицы C.
Алгоритм выполняется за q шагов, где q – размерность вычислительной решетки. Каждый шаг состоит из следующих действий:
на вычислительном узле решетки с индексами (i,j) производится умножение блоков A(i,i) и B(i,j).
Циклическое смещение блоков матрицы C вправо на 1 узел по горизонтали решетки.
Циклическое смещение блоков матрицы B вверх на 1 узел по вертикали решетки.
Результат умножения матриц хранится в матрицы C, блоки которой подлежат смещению. Поэтому по завершению нужно выровнять матрицу до выходного отображения блоков.
Анализ эффективности
Время выполнения п.1), п. 2) или п.3) просчитывается по формуле (8). Время умножения матриц в одном блоке – формула (9). Время циклического сдвига для п. с) и b) – (10). После выполнения шагов матрицы и необходимо выровнять до выходного отображения блоков на узле вычислительной решетке. Время выполнения рассчитывается по (8).
Суммарное время выполнения алгоритма:
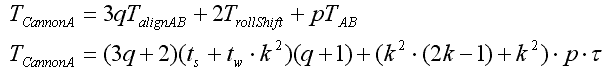
Отсюда получаем ускорение параллельного алгоритма и эффективность использования параллельным алгоритмом процессоров при решении задачи:
Сравнительный анализ алгоритмов
Отличия вышерассмотренных алгоритмов состоит в коммуникационных затратах. Рассмотрим графики поведения алгоритмов, на которых черным цветом представлен алгоритм вычисления матричного произведения с сохранением отображения блоков матрицы-результата C, а серым – алгоритм вычисления матричного произведения с сохранением отображения блоков матрицы A. На Рис.1 отображается поведение функции времени для фиксированных матриц, n=10000, в зависимости от количества узлов решетки. На Рис.2 показана зависимость функции времени для фиксированного числа узлов решетки, p=10000, в зависимости от размера матриц. На Рис.3 показано поведение функции ускорения для фиксированных матриц, n=10000, в зависимости от количества узлов решетки. На Рис.4 показана зависимость функции ускорения фиксированного числа узлов решетки, p=10000, в зависимости от размера матриц.
Рис.2 – График зависимости времени выполнения от количества узлов
Рис.3 – График зависимости времени выполнения от размера матрицы
Рис.4 – График зависимости ускорения от количества узлов
Рис.5 – График зависимости ускорения от размера матрицы
Выводы
В работе были проведены исследования эффективности и масштабируемости алгоритмов семейства Кэннона. Два алгоритма показывали близкие значения в отдельных ситуациях, однако наиболее эффективным с точки зрения времени выполнения оказался алгоритм вычисления матричного произведения с сохранением отображения блоков матрицы-результата C, что было определено, анализируя графики зависимостей.
В дальнейшем при выполнении магистерской диссертации будет проведен анализ непосредственно методов решения задачи Коши, также будет разработана программная система для решения задачи Коши одношаговыми методом. Использование разрабатываемой программной системы позволит оценить показатели эффективности и точность параллельного решения задачи Коши исследуемым методом на практике.
Список литературы
Гергель В.П. Теория и практика параллельных вычислений
http://www.intuit.ru/department/calculate/paralltp/Назарова И.А. Анализ масштабируемости параллельных алгоритмов численного решения задачи Коши. Наукові праці ДонНТУ серія "Інформатика, кібернетика та обчислювальна техніка", 2009г.
Gupta A., Kumar V. Scalability of parallel algorithm for matrix multiplication // Technical report TR-91-54, Department of CSU of Minneapolis, 2001
Воеводин В.В. Вычислительная математика и структура алгоритмов.-М.: Изд-во МГУ, 2006.-112 с.
http://www.parallel.ru/info/parallel/voevodin/В.П. Гергель, Р.Г. Стронгин. Основы параллельных вычислений для многопроцессорных вычислительных систем. Учебное пособие. Издание 2-е, дополненное. Издательство Нижегородского госуниверситета. Нижний Новгород. 2003г
http://www.software.unn.ru/ccam/files/HTML_Version/index.htmlЛ.П. Фельдман, Д.А. Завалкин. Эффективность и масштабируемость параллельных одношаговых блочных методов решения задачи Коши. Донецкий национальный технический университет, г. Донецк, Украина
В.П. Гергель, В.А. Фурсов. Лекции по параллельным вычислениям: учеб. пособие / В.П. Гергель, В.А.Фурсов. – Самара: Изд-во Самар. гос. аэрокосм. ун-та, 2009. – 164 с.
http://oi.ssau.ru/lecparall.pdfВ.Н. Дацюк, А.А. Букатов, А.И. Жегуло. Ростовский государственный университет. Методическое пособие по курсу "Многопроцессорные системы и параллельное программирование"
http://rsusu1.rnd.runnet.ru/tutor/method/m1/content.htmlИнформационно-аналитический центр о параллельных вычислениях
http://parallel.ru/Ian T. Foster. Designing and Building Parallel Programs
http://www.imamod.ru/~serge/arc/stud/DBPP/text/book.html
Важное замечание
На момент написания данного реферата магистерская работа еще является не завершенной. Предполагаемая дата завершения: декабрь 2011 г., ввиду чего полный текст работы, а также материалы по теме могут быть получены у автора или его руководителя только после указанной даты.