Abstract
- Introduction
- Topicality
- Scientific and practical significance
- Expected practical results
- Cauchy problem
- Efficiency and scalability of parallel algorithms for block matrix multiplication
- Characteristics of parallel computing
- Conclusions
- References
Introduction
In today's world one of the main computers are parallel computing systems. This is due to the need to effectively address the fundamental scientific and engineering problems that require vast amounts of computing with powerful computing resources.
With increasing computational power of computing systems, today's supercomputers, clusters of workstations it became possible solution of many problems that involve huge amounts of computing performance in a reasonable time. This is achieved by parallelizing the algorithms and the use of multiprocessor systems.
Parallel computations, when the same time holds multiple data processing operations carried out, mainly due to the introduction of redundancy of functional units (multiprocessor). In this case, you can reach speed up the process of solving computational problems, if implemented separation algorithm applied to information independent of and organize the implementation of each part of the calculations on different processors. This approach allows to perform the necessary calculations with less time and opportunity to obtain the maximum possible speed is limited only by the number of available processors and the number of "independent" part of the calculations performed [1].
However, when developing parallel algorithms for numerical solution of any complex dynamic problems of the important point is to analyze the quality of the use of parallelism, which normally consists in the evaluation of the resulting acceleration of the computing process (reducing the time required to solve the problem) [1].
Topicality
Application of parallel computing systems is the strategic direction of computing. This circumstance is due not only fundamental limitation the maximum possible performance of conventional serial computers, but almost constant presence of computational tasks for which the capacity of existing computer equipment always is not enough [1].
The efficiency of the implementation of parallel computing depends largely on the adequacy of the mapping calculation algorithm on a parallel architecture, matching the properties of the algorithm and the features of a supercomputer, and the implementation of the parallel algorithm can not be studied in isolation from the parallel computing system on which it is implemented.
Scientific and practical significance
As is well known ordinary differential equations are the basis for modern engineering problems. It is therefore important to investigate the one-step methods for solving the Cauchy problem with the mapping on a multiprocessor architecture and to analyze the scalability of parallel algorithms.
Expected practical results
While working on graduate work is planned to analyze the parallel one-step methods for the Cauchy problem, namely to investigate the scalability of methods to construct a function isoefficiency and follow the dependence of the number of processors of the computing system the size of the task.
Cauchy problem
Cauchy problem for systems of ordinary differential equations (SODE) of first order with known initial conditions is (1). There are many parallel methods for solving the Cauchy problem for SODE first order [8].
However, they all include a matrix multiplication. Therefore, an important step is to study the parallel matrix multiplication.
Efficiency and scalability of parallel algorithms for block matrix multiplication
Matrix multiplication - one of the basic operations which is performed when solving problems and at the same time, it is quite time consuming with the operating and commutative point of view. Therefore, the efficiency of solving this problem - an important factor.
Topology of the grid and hypercube are the most suitable for carrying out such operations. For this topology, the calculation of matrix arithmetic operations can be reduced to perform operations with blocks of matrices.
There are several such algorithms. In this paper we consider a family of algorithms of Cannon, which is based on a block decomposition of matrices.
In Cannon's algorithm the two original matrices A and B and the results matrix C is divided into blocks. Cannon family alters the mapping of blocks of two of the three matrices, which take part in the computation of the product.
Let the number of columns / rows of the matrix n is divisible by the number of lattice sites p. Number of lattice sites along the vertical / horizontal is q. If we represent the matrix in the form of square blocks of size k = n / q elements, then each node can be uniquely placed in correspondence with a block.
Characteristics of parallel computing
Consider the conventional and most used in parallel computing performance:
– The time consistent implementation of the algorithm,
the time required to solve the problem of a given size on a single processor using the best sequential algorithm; 
– The time for solving the problem of a
given size using a parallel algorithm on a parallel computer of p processors without taking into account exchange transactions,
in fact, during the implementation of algorithms on a parallel computer;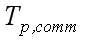 
– Communication cost, complexity of the algorithm or
runtime interprocessor exchange operations in the implementation of a parallel algorithm for solving a given size;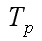 
– Time of parallel execution, the total time of implementation
of the parallel algorithm on a parallel architecture: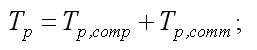
– The share exchange transactions to the total execution
time of parallel algorithm: 
– Maximum degree of parallelism, the maximum number of
processors used
in the implementation of the parallel algorithm; 
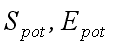– Coefficients of the potential speedup and efficiency
(excluding exchange operations); S, E - real rates of acceleration and efficiency, parallel algorithm (taking into account currency
exchange operations)[2].
Dynamic characteristics of parallel algorithms depend on many variables, such as the number of processors of the computing system p and the dimension of the problem being solved m.
Also important characteristic is the acceleration, which shows how many times faster than the parallel algorithm running on a parallel computer of p processors over the sequential version of the solution.
The acceleration factor is defined as the ratio of the time solving the problem on a uniprocessor computer system at the time of execution of the parallel algorithm. Distinguish between potential and real parallelism, and consequently, the corresponding rates of acceleration. Coefficient of acceleration potential takes into account only the inner, hidden parallelism method for solving the problem without taking into account exchange operations and other overhead costs:
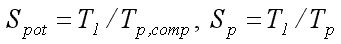
By scalability we mean the ability of a parallel system to increase productivity by increasing the number of processors. For a fixed problem size and the number of processors - parallel efficiency decreases. For a fixed number of processors and increasing the size of the problem - the parallel efficiency increases. Parallel algorithm is called scalable if an increase in the number of processors can increase the dimension of the problem so as to maintain a constant parallel efficiency.
Another important characteristic of the parallel algorithm is the efficiency ratio (efficiency). The effectiveness of the use of a parallel algorithm for solving the problem of processors is calculated as follows:
Efficiency ratio determines the average share of run-time algorithm in which processors are actually used to solve the problem, ie the quality of the parallel loading of equipment. There are several approaches to quantify the properties of scalability of the algorithm. The most used metric is proposed and based on the introduction of the function of equal effectiveness or isoefficiency. isoefficiency Analysis - a measure of the scalability of parallel algorithms. To characterize the properties of scalability evaluate the overhead (time T0) the organization of interaction between processors, synchronization of parallel computing, etc.:
isoefficiency function is one such metric of scalability, which is a measure of the algorithmic ability to effectively use more processors on a parallel architecture. Function isoefficiency combination of the parallel algorithm and parallel architecture depends on the dimension of the problem and the number of processors needed to maintain a fixed performance or achievements of the acceleration increases proportionally with the number of processors [3]. The effectiveness of the parallel system is considered as
Conclusions
In this paper, I studied the efficiency and scalability of algorithms for a family of Cannon. In the future in my master's work I will analyze the direct methods for solving the Cauchy problem, I will also develop a software system for solving the Cauchy-step method. Using the developed software system will evaluate the efficiency of the parallel solution of the differnt methods of Cauchy problem in practice.
References
Gergel V.P. Theory and practice of parallel computing
http://www.intuit.ru/department/calculate/paralltp/Nazarova I.A. Analysis of scalability of parallel algorithms for numerical solution of the Cauchy problem. Naukov³ prats³ DonNTU ser³ya "²nformatika, k³bernetika that obchislyuvalna tehn³ka, 2009.
Gupta A., Kumar V. Scalability of parallel algorithm for matrix multiplication // Technical report TR-91-54, Department of CSU of Minneapolis, 2001
Voevodin VV Computational Mathematics and structure algoritmov.-M.: Izdatel'stvo MGU, 2006.-112.
http://www.parallel.ru/info/parallel/voevodin/V.P. Gergel, R.G. Strongin. Foundations of parallel computing for multiprocessor systems. Textbook. 2 nd edition, enlarged. Publisher Nizhni Novgorod State University. Nizhny Novgorod. 2003
http://www.software.unn.ru/ccam/files/HTML_Version/index.htmlL.P. Feldman, D.A. Zavalkin. Efficiency and scalability of parallel one-step block method for solving the Cauchy problem. Donetsk National Technical University, Donetsk, Ukraine
V.P. Gergel, V.A. Fursov. Lectures of parallel computation: study. Benefit / V.P. Gergel, V.A. Fursov. - Samara: Izd-vo Samar. state. Aerospace. Press, 2009. - 164.
http://oi.ssau.ru/lecparall.pdfV.N. Datsyuk, A.A. Bukatov, A.I. Zhegulo. Rostov State University. Methodological manual for the course "Multiprocessor systems and parallel programming"
http://rsusu1.rnd.runnet.ru/tutor/method/m1/content.htmlInformation-Analytical Center of parallel computing
http://parallel.ru/Ian T. Foster. Designing and Building Parallel Programs
http://www.imamod.ru/~serge/arc/stud/DBPP/text/book.html
Important Note
At the time of writing this abstract master work is still not complete. Expected completion date: December 2011, thus giving the full text of the work, as well as materials on the subject can be obtained from the author or his manager after that date.