Реферат з теми випускної роботи
- Введення
- Актуальність
- Наукове та практичне значення
- Плановані практичні результати
- Задача Коші
- Ефективність і масштабованість паралельних алгоритмів блочного матричного добутоку
- Основні показники паралельних обчислень
- Аналіз алгоритмів Кеннона
- Висновки
- Список літератури
Введення
У сучасному світі одним з основних напрямів обчислювальної техніки є паралельні обчислювальні системи. Це пов'язано з потребою ефективного вирішення фундаментальних наукових та інженерних завдань, які вимагають величезних обсягів обчислень, з використанням потужних обчислювальних ресурсів.
Зі зростанням обчислювальних потужностей обчислювальних систем, сучасних суперкомп'ютерів, кластерів робочих станцій стало можливим вирішення багатьох завдань, які передбачають виконання величезних обсягів обчислень за прийнятний час. Це досягається шляхом розпаралелювання алгоритмів та використання багатопроцесорних систем.
Організація паралельності обчислень, коли в один і той же момент виконується одночасно кілька операцій обробки даних, здійснюється, в основному, за рахунок введення надмірності функціональних пристроїв (многопроцессорности). У цьому випадку можна досягти прискорення процесу розв'язання обчислювальної задачі, якщо здійснити поділ вживаного алгоритму на інформаційно незалежні частини і організувати виконання кожної частини обчислень на різних процесорах. Подібний підхід дозволяє виконувати необхідні обчислення з меншими витратами часу, і можливість отримання максимально-можливого прискорення обмежується тільки кількістю наявних процесорів і кількістю "незалежних" частин у виконуваних обчисленнях [1].
Однак при розробці паралельних алгоритмів чисельного рішення будь-яких складних динамічних завдань важливим моментом є аналіз якості використання паралелізму, що складається звичайно в оцінці одержуваного прискорення процесу обчислень (скорочення часу виконання завдання) [1].
Актуальність
Застосування паралельних обчислювальних систем є стратегічним напрямком розвитку обчислювальної техніки. Ця обставина викликано не тільки принциповим обмеженням максимально можливого швидкодії звичайних послідовних ЕОМ, але і практично постійною наявністю обчислювальних завдань, для вирішення яких можливостей існуючих засобів обчислювальної техніки завжди виявляється недостатньо [1].
Ефективність реалізації паралельних обчислень залежить від адекватності відображення обчислювального алгоритму на паралельну архітектуру, узгодження властивостей алгоритму і особливостей суперкомп'ютера, також виконання паралельного алгоритму не може бути вивчене у відриві від паралельної обчислювальної системи, на якій він реалізований.
Наукове та практичне значення
Як відомо звичайні диференціальні рівняння є основою сучасних інженерних завдань. Саме тому важливо дослідити однокрокові методи розв'язання задачі Коші з відображенням на багатопроцесорної архітектурі і провести аналіз масштабованості паралельних алгоритмів.
Плановані практичні результати
У процесі роботи над дипломною роботою планується проаналізувати паралельні однокрокові методи задачі Коші, а саме дослідити масштабованість методів, побудувати функцію ізоеффектівності і простежити залежність кількості процесорів обчислювальної системи від розміру розв'язуваної задачі.
Задача Коші
Задача Коші для системи звичайних диференціальних рівнянь (СЗДР) першого порядку з відомими початковими умовами має вигляд (1). Існує багато паралельних методів рішення завдання Коші для СЗДР першого порядку [8].

Проте всі вони включають в себе матричний добуток. Тому важливим етапом є дослідження паралельного матричного добутку.
Ефективність і масштабованість паралельних алгоритмів блочного матричного добутоку
Матричний добуток – одна з основних операцій, що виконується при вирішенні завдань і в той же час воно є досить трудомістким з операційної та комутативною точки зору. Тому ефективність вирішення цієї задачі – важливий фактор.
Топологія решітка і гіперкуб є найбільш придатними для реалізації таких операцій. Для такої топології обчислення матричних арифметичних операцій можна звести до виконання операцій з блоками матриць
Існує кілька таких алгоритмів. У даній роботі розглядається сімейство алгоритмів Кеннона, яке засноване на блочному розбитті матриць.
В алгоритмі Кеннона дві вихідні матриці A і B і матриця результат C поділяються на блоки. Родини Кеннона змінює відображення блоків двох з трьох матриць, які беруть участь в обчисленні добутку.
Нехай кількість стовпців/рядків матриці n кратно числу вузлів решітки p. Кількість вузлів решітки по вертикалі / горизонталі дорівнює q. Якщо уявити матриці у вигляді квадратних блоків розміром k=n/q елементів, то кожному вузлу можна однозначно поставити у відповідність такий блок.
Основні показники паралельних обчислень
Розглянемо загальноприйняті і найбільш використовувані в паралельних обчисленнях показники:
 – час послідовного виконання алгоритму, час,
необхідний для вирішення завдання заданого розміру на одному процесорі за допомогою найкращого послідовного алгоритму;
– час послідовного виконання алгоритму, час,
необхідний для вирішення завдання заданого розміру на одному процесорі за допомогою найкращого послідовного алгоритму;  – час виконання завдання заданого розміру
з використанням паралельного алгоритму на паралельному комп'ютері з p процесорів без обліку обмінних
операцій, власне, час реалізації обчислень на паралельному комп'ютері;
– час виконання завдання заданого розміру
з використанням паралельного алгоритму на паралельному комп'ютері з p процесорів без обліку обмінних
операцій, власне, час реалізації обчислень на паралельному комп'ютері;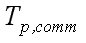 – комунікаційна трудомісткість, складність алгоритму або час виконання міжпроцесорних
операцій обміну при реалізації паралельного алгоритму розв'язання задачі заданого розміру;
– комунікаційна трудомісткість, складність алгоритму або час виконання міжпроцесорних
операцій обміну при реалізації паралельного алгоритму розв'язання задачі заданого розміру;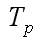 – час паралельного виконання, загальний час
реалізації паралельного алгоритму на паралельній архітектурі:
– час паралельного виконання, загальний час
реалізації паралельного алгоритму на паралельній архітектурі: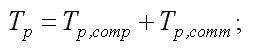
 – частка обмінних операцій до загального часу виконання паралельного алгоритму:
– частка обмінних операцій до загального часу виконання паралельного алгоритму: 
 – максимальна ступінь паралелізму, максимальна кількість процесорів,
використовуваних у процесі виконання паралельного алгоритму;
– максимальна ступінь паралелізму, максимальна кількість процесорів,
використовуваних у процесі виконання паралельного алгоритму;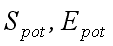 – коефіцієнти потенційного прискорення
та ефективності (без урахування операцій обміну); S, E – коефіцієнти реального прискорення та ефективності,
паралельного алгоритму (з урахуванням обмінних операцій) [2].
– коефіцієнти потенційного прискорення
та ефективності (без урахування операцій обміну); S, E – коефіцієнти реального прискорення та ефективності,
паралельного алгоритму (з урахуванням обмінних операцій) [2].
Динамічні характеристики паралельних алгоритмів залежать від багатьох змінних, таких як кількість процесорів обчислювальної системи p і розмірності розв'язуваної задачі m.
Також важливою характеристикою є прискорення, яка показує у скільки разів швидше паралельний алгоритм виконується на паралельному комп'ютері з p процесорів в порівнянні з послідовним варіантом вирішення завдання.
Коефіцієнт прискорення визначається, як відношення часу рішення задачі на однопроцесорній обчислювальної системі до часу виконання паралельного алгоритму. Розрізняють потенційний і реальний паралелізм, а, отже, і відповідні коефіцієнти прискорення. Коефіцієнт потенційного прискорення враховує тільки внутрішній, прихований паралелізм методу розв'язання задачі без урахування операцій обміну та інших накладних витрат:
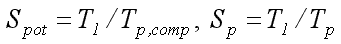
Під масштабованістю розуміється здатність паралельної системи до збільшення продуктивності при збільшенні кількості процесорів. При фіксованому розмір задачі і зростанні числа процесорів – паралельна ефективність падає. При фіксованому числі процесорів і зростанні розміру задачі – паралельна ефективність зростає.Паралельний алгоритм називається масштабованим, якщо при збільшенні кількості процесорів можна збільшувати розмірність задачі так, щоб підтримати паралельну ефективність постійною.
Наступною важливою характеристикою паралельного алгоритму є коефіцієнт ефективності (efficiency). Ефективність використання паралельним алгоритмом процесорів при вирішенні завдання обчислюється таким чином:

Коефіцієнт ефективності визначає середню частку часу виконання алгоритму, протягом якого процесори реально використовуються для вирішення завдання, тобто якість завантаження паралельного обладнання. Існує декілька підходів для кількісної оцінки властивостей масштабованості алгоритму. Найбільш вживаною є метрика, запропонована і заснована на введенні функції рівній ефективності або ізоеффектівності. Ізоеффектівний аналіз – міра масштабованості паралельних алгоритмів. Для характеристики властивостей масштабованості оцінюють накладні витрати (час T0) на організацію взаємодії процесорів, синхронізацію паралельних обчислень і т.п.:

Функція ізоеффектівності є одним з таких метрики масштабованості, яка є мірою алгоритмічної здатності ефективно використовувати більшу кількість процесорів на паралельній архітектурі. Функція ізоеффектівності поєднання паралельного алгоритму і паралельні архітектури залежить від розмірності задачі і числа процесорів, необхідних для підтримки фіксованого ефективності або досягнення прискорення, що збільшується пропорційно зі зростанням числа процесорів [3]. Ефективність паралельної системи рахується, як

Аналіз алгоритмів Кеннона
Алгоритм обчислення матричного добутку зі збереженням відображення блоків матриці-результату С
Алгоритм включает в себя шаги:блоки рядків матриці A зсуваються циклічно вліво на i вузлів по горизонталі, де i – індекс рядка матриці A .
блоки стовпців матриці B зсуваються циклічно вгору на j вузлів по вертикалі, де j – індекс стовпця матриці B.

Малюнок 1 – Циклічне зсування блоків
Алгоритм виконується за q кроків, де q – розмірність обчислювальної решітки. Кожен крок складається з наступних дій:
На обчислювальному вузлі решітки з індексами (i,j) рахується добуток блоків A(i,j) и B(i,j).
Циклічне зміщення блоків матриці A вліво на 1 вузол по горизонталі решітки.
Циклічне зміщення блоків матриці B вгору на 1 вузол по вертикалі решітки.
Результат добутку матриць зберігається в матриці C, блоки якої не підлягають зсуву.
Аналіз ефективності
Час виконання п.1) або п.2) згідно [1] можна розрахувати за формулою:
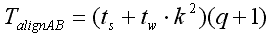
Час матричного добутку в одному блоці:

Час циклічного зсуву для п. с) і b):

Сумарний час виконання алгоритму:

Звідси отримуємо прискорення паралельного алгоритму і ефективність використання паралельним алгоритмом процесорів під час вирішення завдання:

Алгоритм обчислення матричного твори зі збереженням відображення блоків матриці A
Алгоритм включає в себе кроки:блоки рядків матриці B зсуваються циклічно вправо на i вузлів по горизонталі, де i – індекс рядка матриці B .
блоки стовпців матриці B зсуваються циклічно вгору на j вузлів по вертикалі, де j – індекс стовпця матриці B.
блоки рядків С зсуваються циклічно вправо на i вузлів по горизонталі, де i – індекс рядка матриці С .
Алгоритм виконується за q кроків, де q – розмірність обчислювальної решітки. Кожен крок складається з наступних дій:
На обчислювальному вузлі решітки з індексами (i,j) рахується добуток блоків A(i,j) и B(i,j).
Циклічне зміщення блоків матриці С праворуч на 1 вузол по горизонталі решітки.
Циклічне зміщення блоків матриці B вгору на 1 вузол по вертикалі решітки.
Результат добутку матриць зберігається в матриці C, блоки якої підлягають зсуву. Тому по завершенню потрібно вирівняти матрицю до вихідного відображення блоків.
Аналіз ефективності
Час виконання п.1), п. 2) або п.3) прораховується за формулою (8). Час множення матриць в одному блоці – формула (9). Час циклічного зсуву для п. с) і b) – (10). Після виконання кроків матриці і необхідно вирівняти до вихідного відображення блоків на вузлі обчислювальної решітці. Час виконання розраховується за (8).
Сумарний час виконання алгоритму:
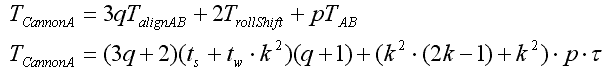
Звідси отримуємо прискорення паралельного алгоритму і ефективність використання паралельним алгоритмом процесорів під час вирішення завдання:

Порівняльний аналіз алгоритмів
Відмінності вищерозглянутих алгоритмів полягає в комунікаційних витратах. Розглянемо графіки поведінки алгоритмів, на яких чорним кольором представлений алгоритм обчислення матричного добутку зі збереженням відображення блоків матриці-результату C, сірим – алгоритм обчислення матричного добутку зі збереженням відображення блоків матриці A. На малюнку 1 відображається поведінку функції часу для фіксованих матриць, n=10000, в залежності від кількості вузлів решітки. На малюнку 2 показана залежність функції часу для фіксованого числа вузлів решітки, p=10000, в залежності від розміру матриць. На малюнку 3 показано поведінку функції прискорення для фіксованих матриць, n=10000, в залежності від кількості вузлів решітки. На малюнку 4 показана залежність функції прискорення фіксованого числа вузлів решітки, p=10000, в залежності від розміру матриць.

Малюнок 2 – Графік залежності часу виконання від кількості вузлів

Малюнок 3 – Графік залежності часу виконання від розміру матриці

Малюнок 4 – Графік залежності прискорення від кількості вузлів

Малюнок 5 – Графік залежності прискорення від розміру матриці
Висновки
У роботі були проведені дослідження ефективності і масштабованості алгоритмів сімейства Кеннона. Ці два алгоритми показували близькі значення в окремих ситуаціях, однак найбільш ефективним з точки зору часу виконання виявився алгоритм обчислення матричного добутку зі збереженням відображення блоків матриці-результату C, що було визначено, аналізуючи графіки залежностей.
У найбутньому під час виконанні магістерської роботи буде проведено аналіз безпосередньо методів рішення задачі Коші, також буде розроблена програмна система для вирішення задачі Коші однокроковими методом. Використання програмної системи дозволить оцінити показники ефективності і точність паралельного розв'язання задачі Коші досліджуваним методом на практиці.
Список літератури
Гергель В.П. Теорія та практика паралельних обчислювань
http://www.intuit.ru/department/calculate/paralltp/Назарова И.А. Аналіз масштабованості паралельних алгоритмів чисельного розв'язання задачі Коші. Наукові праці ДонНТУ серія "Інформатика, кібернетіка та обчіслювальна техніка", 2009г.
Gupta A., Kumar V. Scalability of parallel algorithm for matrix multiplication // Technical report TR-91-54, Department of CSU of Minneapolis, 2001
Воєводин В.В. Обчислювальна математика і структура алгоритмів.-М.: Изд-во МГУ, 2006.-112 с.
http://www.parallel.ru/info/parallel/voevodin/В.П. Гергель, Р.Г. Стронгін. Основи паралельних обчислень для багатопроцесорних обчислювальних систем. Навчальний посібник. Видання 2-е, доповнене. Видавництво Нижегородського держуніверситету. Нижній Новгород. 2003г
http://www.software.unn.ru/ccam/files/HTML_Version/index.htmlЛ.П. Фельдман, Д.А. Завалкін. Ефективність і масштабованість паралельних однокрокових блокових методів рішення задачі Коші. Донецький національний технічний університет, м. Донецьк, Україна
В.П. Гергель, В.А. Фурсов. Лекції з паралельних обчислень: навч. посібник / В.П. Гергель, В. А. Фурсов. - Самара: Вид-во Самар. держ. аерокосм. ун-ту, 2009. – 164 с.
http://oi.ssau.ru/lecparall.pdfВ.Н. Дацюк, А.А. Букатов, А.И. Жегуло. Ростовський державний університет. Методичний посібник з курсу "Багатопроцесорні системи та паралельне програмування "
http://rsusu1.rnd.runnet.ru/tutor/method/m1/content.htmlІнформаційно-аналітичний центр про паралельні обчислення
http://parallel.ru/Ian T. Foster. Designing and Building Parallel Programs
http://www.imamod.ru/~serge/arc/stud/DBPP/text/book.html
Важливе зауваження
На момент написання даного реферату магістерська робота ще є не завершеною. Передбачувана дата завершення: грудень 2011 р., тому повний текст роботи, а також матеріали за темою можуть бути отримані у автора або його керівника тільки після зазначеної дати.
