Реферат на тему випускної роботи

1 Введення

2 Аналіз завдання розбиття простору з використанням деревовидних карт

   2.1 Деревоподібні карти, як метод відображення інформації

   2.2 Параметри для оцінки ефективності розбиття простору деревоподібної карти

3 Огляд існуючих алгоритмів розбиття простору з використанням деревовидних карт

   3.1 Алгоритм "горизонталь-вертикаль"

   3.2 Квадратичні деревоподібні карти

   3.3 Впорядковані деревоподібні карти

   3.4 Смуговий алгоритм

   3.5 Квантові деревоподібні карти

4 Висновки. Цілі і завдання подальшого дослідження

5 Література

1 Введення

Дослідження залежностей і закономірностей у геоінформаційних даних є складним завданням через їх великий розмір. Дані можуть бути різної природи і з різних джерел. Необхідно розробити методи ефективної взаємодії комп'ютера та електронної обробки, і людського зору, методи аналізу та візуалізації даних, що стимулюють виявлення залежностей, вироблення гіпотез і вилучення знань з даних.

Геовізуалізація – метод дослідження просторових знань, прихованих в багатовимірних географічних і часових даних через взаємодію з картою і графом. Геовізуалізація це не просто пасивний процес перегляду та читання карт. Це активний процес, що включає сортування, виділення, фільтрацію і перетворення даних для визначення залежностей і відносин. Карти та графіки в цьому контексті роблять більше, ніж «відображають дані», вони є активними інструментами в процесі мислення користувача [1].

Підходи до геовізуалізаціі

Традиційним підходом, що застосовується при геовізуалізаціі, є пряме відображення кожного запису з масиву даних; після цього аналітик вивчає ці дані і намагається визначити якісь залежності. Однак безліч джерел і розмір даних ростуть з кожним днем, що значно ускладнює завдання аналітика. Подання даних (на папері, моніторі або іншому пристрої) може стати нерозбірливим через візуальної перевантаженості, великих обсягів даних і інформації різної природи. У користувача можуть виникнути проблеми зі сприйняттям, відстеженням і розумінням безлічі візуальних елементів, які змінюються паралельно. Безліч методів було розроблено для візуального аналізу просторових даних шляхом прямого відображення. Однак, малоймовірно, що дані методи зможуть ефективно вирішити проблему перевантаженості зображення даними. Підходи, що застосовуються при геовізуалізаціі великих обсягів даних:

- відображення і візуалізація абстрактного набору даних, отриманого в результаті попередньої обробки даних;

- розробка різного роду відображень для використання простору карти більш ефективно.

Серед основних методів попередньої обробки даних можна виділити:

- побудова кореляційної матриці та визначення значущих чинників;

- очищення і перетворення даних;

- факторний аналіз, аналіз головних компонент;

- сортування, агрегація, фільтрація і.т.д.

До методів, які використовують простір карти більш ефективно, відносять:

- карти щільності;

- гістограми, діаграми, графіки, тимчасові ряди;

- анімація;

- просторово-часової куб;

- кільцеві карти, деревоподібні карти, і.т.д.

У загальному вигляді процес геовізуалізаціі зображений на мал. 1: основу піраміди це сирі дані про предметну область, з-за їх величезного розміру їх дуже складно аналізувати і працювати з ними. Верхівка піраміди це дані отримані після геовізуалізаціі: їх на порядок менше і увагу користувача концентрується на найважливішому для прийняття рішення.

Малюнок 1 – Процес геовізуалізаціі

У даній роботі будуть розглянуті деревоподібні карти, їх ефективність при відображенні великих обсягів даних і області застосування.

Актуальність роботи:

Деревоподібні карти використовуються для відображення широкого спектру даних ієрархічної природи. NewsMap – онлайн програма, яка відображає новини Google у вигляді деревоподібної карти. Колір прямокутника визначає тип новини, а його розмір – кількість статей в інтернеті по даній темі. Ще одним дуже хорошим прикладом використання деревовидних карт є «Карта ринку»на сайті Smartmoney.com. Цьому додатку, компанії розділені по різних регіонах, в залежності від сектора ринку, в якому вони знаходяться. Розмір кожного прямокутника, що характеризує компанію, залежить від її частки на ринку. Колір прямокутників також несе в собі інформацію, і знаходиться в межах від червоного до зеленого, він відповідає за динаміку зростання або спаду тієї чи іншої компанії або сфери ринку в цілому. Також існує безліч додатків використовують деревоподібні карти для:

- відображення файлової системи;

- відображення фотографій;

- медицина, відображення геному людини;

- перетворення даних з формату Ecxel в деревовидну карту;

2 Аналіз задачі розбиття простору з використанням деревовидних карток

Деревоподібні карта – метод відображення ієрархічних даних великих розмірів. Вони ефективно поєднують в собі діаграму Венна і секторну діаграму. Спочатку розроблені для відображення файлів жорсткого диска, зараз деревоподібні карти застосовуються в багатьох галузях, починаючи від фінансового аналізу і закінчуючи спортивними оглядами і медициною [2].

2.1 Деревоподібні карти, як метод відображення інформації

Бен Шнідерман придумав нове подання даних у вигляді деревоподібної карти для більш наочного відображення файлової системи свого комп'ютера. Традиційний підхід для відображення деревовидних структур показує вузли та рівні ієрархії у вигляді папок і з'єднують стрілок (мал.1). Це працює, і досить добре, для деревовидних структур малого розміру. Однак, якщо цей самий підхід застосовується для дерев більшого розміру, з сотнями і тисячами вузлів і багатьма рівнями ієрархії, на екрані з'являється хаос у вигляді безлічі папок і ліній.

На початку, деревоподібна карта складається з одного великого прямокутника, і потім відбувається поділ цієї прямокутника на області меншого розміру рекурсивно. Початковий прямокутник представляє корінь дерева. Він поділяється на сукупність прямокутників меншого розміру, розділених горизонтально, кожен з яких є дочірнім по відношенню до кореня дерева. Далі процес повторюється, на кожному рівні ієрархії напрямок поділу змінюється з горизонтального на вертикальне, і навпаки [5].

Малюнок 2 – Традиційне відображення даних деревоподібної структури

На мал.2 показано перетворення даних, представлених у вигляді дерева в деревовидну карту.

Малюнок 3 – Перетворення даних: дерево в деревовидну карту

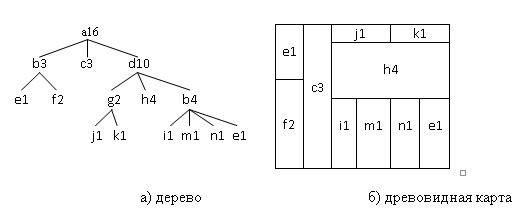
На даний момент у деревовидних картах використовуються такі підходи для передачі інформації:

- розмір прямокутників;

- колір прямокутників;

- анотації.

Відображення дерев у вигляді деревоподібної карти має 2 переваги. Перше – це те, що дуже легко бачити ієрархічну структуру, показані зв'язки між рівнями. Дочірні рівні знаходяться всередині свого батька. Наступною перевагою є те, що при такому поданні простір карти використовується дуже ефективно. Початковий прямокутник повністю заповнюється прямокутниками меншого розміру.

Деревовидна карта є, особливо, ефективним засобом відображення дерев, якщо кожен лист дерева має вагу, асоційований з ним. В якості ваги може виступати: розмір файлу, у разі Шнідермана, фізичну вагу, грошова вартість, вміст цукру і.т.д. Залежно від ваги того чи іншого листа, він буде займати більше чи менший простір на карті [3].

2.2 Параметри для оцінки ефективності розбиття простору деревоподібної картки

Ключовим аспектом при створенні деревовидних карт є алгоритм, що застосовується для створення вкладених прямокутників, що складають карту. Ефективність алгоритму визначається наступними параметрами:

- середнє співвідношення сторін прямокутників (середній коефіцієнт пропорційності);

- динамічний коефіцієнт зміни;

- легкість для читання карти;

- упорядкованість даних.

Середній коефіцієнт пропорційності визначається за формулою:

- AAR (Average Aspect Ratio) – середній коефіцієнт пропорційності;

- l – ширина прямокутника;

- h – висота прямокутника;

- n – загальна кількість прямокутників.

Чим ближче коефіцієнт пропорційності окремого прямокутника до 1, тим він ближче за формою до квадрата. І, відповідно, чим ближче середній коефіцієнт пропорційності до 1, тим більше «квадратної» є карта. Людині складно працювати з витягнутими прямокутниками: прямокутники з різними коефіцієнтами пропорційності складно порівнювати між собою, додавати анотації до них і навіть просто побачити на карті.

Середній динамічний коефіцієнт зміни визначається за формулою:

- ADCH (Average Dynamic Coefficient of Change) – середній динамічний коефіцієнт зміни;

- n – загальна кількість прямокутників;

- R – прямокутник, визначається 4-ма числами (x, y, w, h);

- d (R1, R2) – відстань між прямокутниками, визначається за формулою:

- x1, y1 – координати верхнього лівого кута 1-го прямокутника;

- w1, h1 – координати нижнього правого кута 1-го прямокутника;

- x2, y2 – координати верхнього лівого кута 2-го прямокутника;

- w2, h2 – координати нижнього правого кута 2-го прямокутника;

Динамічний коефіцієнт зміни характеризує наскільки структура прямокутників однієї картки, відрізняється від іншої. І, отже, чим даний коефіцієнт нижче, тим краще: маленькі зміни в даних призводять лише до невеликих перестроювання карти.

Вибираються «невиважені» середній коефіцієнт пропорційності і динамічної зміни, тобто прямокутники з маленькою площею впливають на дані коефіцієнти, точно так само як і великі. Альтернативою може бути використання «зважених» коефіцієнтів, так як прямокутники більшого розміру вносять більший внесок у загальне візуальне подання. Проте проблема з витягнутими прямокутниками більш характерна прямокутникам меншого розміру і часто доводиться погіршувати коефіцієнт пропорційності великих прямокутників на користь маленьких. Використання «зважених» коефіцієнтів призводить до утворення маленьких, витягнутих прямокутників [10].

Ще параметром, що визначає ефективність алгоритму, є легкість для читання карти – метрика, характеризує наскільки легко і швидко, користувач може знайти цікавить прямокутник. Дану метрику набагато складніше виміряти кількісно. Удобочитаемость залежить від послідовності та прогнозованості розмітки карти. Послідовність дозволяє людині слідувати за шаблоном швидко, не перескакуючи з місця на місце. Прогнозованість фокусує погляд користувача на тому регіоні, де, на його думку, даний прямокутник розташований. Для кількісного вимірювання даної метрики застосовують такі підходи:

- проведення експерименту: показ користувачам одних і тих же даних, згрупованих різним чином (за різними алгоритмами) і виконання відповідних завдань з пошуку потрібного прямокутника. Легкість для читання, потім, може бути виміряна за допомогою інтерв'ю та аналізу часу пошуку;

- Стеження за рухом людського ока під час перегляду карти. Чим частіше людина змінює напрямок перегляду карти або перескакує з місця на місце, тим легкість для читання гірше. Даний підхід є більш механічним, і не вимагає подальших інтерв'ю після перегляду карти.

Кожній карті присвоюється числове значення, що характеризує легкість для читання і показує наскільки легко користувач може знайти цікавить прямокутник.

Деревоподібні карти можуть бути впорядковані та невпорядковані. Для більшості реальних даних порядок важливий і він несе в собі важливу частину інформації, тому ще однією важливою властивістю, що визначає ефективність карти, є упорядкованість даних.

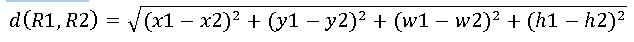
3 Огляд існуючих алгоритмів розбиття простору з використанням деревовидних карток

Ключовим моментом, місцем, в якому відрізняється, більшість алгоритмів, є розрахунок границь прямокутників. В основі більшості алгоритмів лежить послідовний шаблон – обробляється тільки один вузол на кожному кроці. Існують алгоритми, які переглядають наперед список дочірніх вузлів та їх розміщення, при визначенні меж окремого прямокутника. Однак головна ідея всіх алгоритмів залишається однаковою: функція, яка обробляє кожен вузол, в залежності від його розмірів, виділять кожному вузлу деякий простір. Якщо вузол містить дочірні вузли – вони розміщуються всередині батька.

Найбільш широко-використовуваними алгоритмами розбиття простору деревоподібної карти є наступні:

- традиційний алгоритм «горизонталь-вертикаль» (slice-and-dice);

- квадратичний алгоритм (squarified);

- кластер (cluster);

- опорний елемент у центрі (pivot-by-middle);

- опорний елемент за розміром (pivot-by-size);

- опорний елемент за розділеним розміром (pivot-by-split-size);

- поділ по смугах (strip treemap).

3.1 Алгоритм "горизонталь-вертикаль"

Найбільш першим алгоритмом, запропонованим Б. Шнідерманом, був традиційний алгоритм «горизонталь-вертикаль». Простір карти розбивається на вкладені прямокутники, на кожному рівні ієрархії орієнтація ліній (горизонтальна чи вертикальна) змінюється. Приклад перетворення дерева і відображення його у вигляді деревоподібної карти, використовуючи алгоритм «горизонталь-вертикаль» показано на мал.4.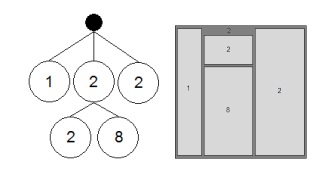

Малюнок 5 – Перетворення дерева в деревовидну карту, алгоритм «горизонталь-вертикаль»

Даний алгоритм легко реалізувати і він є досить ефективним для малого розміру даних, однак зі збільшенням розміру даних даний алгоритм дуже часто призводить до утворення великої кількості витягнутих прямокутників. Дана проблема показана на мал.5 – дуже велика кількість витягнутих прямокутників, з якими складно працювати [9].

Малюнок 6 – Алгоритм «горизонталь-вертикаль»

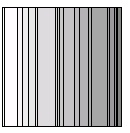
Сильними сторонами даного алгоритму є характеристики «коефіцієнт динамічної зміни» і «легкість для читання». Він також зберігає впорядкованість елементів. Однак з-за дуже високого коефіцієнта пропорційності він дуже рідко використовується на практиці в чистому вигляді, набагато частіше він служить мірою порівняння для інших алгоритмів.

Оцінка складності алгоритму:

Деревовидна карта може бути побудована за один прохід алгоритму по дереву. Тому, вважаючи, що обчислення розміру і кольору прямокутника незмінно, час виконання O (n), де n – кількість вузлів у дереві.

3.2 Квадратичні деревоподібні картки

Як можна розбити початкову область на вкладені прямокутники меншого розміру, так щоб середній коефіцієнт пропорційності був якомога ближче до 1? Список всіх можливих розміщень дуже великий і дана проблема належить до класу NP-складних завдань. Однак, в основі роботи алгоритму квадратичної карти, лежить не повний перебір, не потрібно знаходити оптимальне рішення, необхідно отримати хороше рішення за короткий обчислювальний час [4].

В основі алгоритму квадратичної деревоподібної карти лежить:

- розбивка для всіх підрівнів не проводиться одночасно. Це призводить до значного збільшення обчислювального часу. Замість цього, на кожному рівні розглядаються тільки найближчі дочірні вузли, і проводиться їх розміщення, щоб середнє співвідношення сторін для даного рівня було близько до 1. На наступному рівні ієрархії, початковим буде прямокутник з коефіцієнтом пропорційності близьким до 1 і, отже, гарною відправною точкою для розміщення своїх дочірніх вузлів. Потім процес повторюється рекурсивно;

- прямокутники розміщуються вздовж лінії на вільному місці до тих пір, поки найгірший (найвищий) коефіцієнт пропорційності всіх прямокутників у даній лінії продовжує зменшуватися. Як тільки найгірший коефіцієнт пропорційності досягає свого мінімуму, і додавання ще одного прямокутника призводить до збільшення найгіршого коефіцієнта пропорційності, розміщення даної лінії закінчено, переходимо до наступної.

Приклад:

Припустимо, у нас є прямокутник із шириною 6 і заввишки 4, і даний прямокутник необхідно розділити на менші прямокутники площею 6, 6, 4, 3, 2, 2 і 1. Результат роботи традиційного алгоритму «горизонталь-вертикаль» показано на мал.6, утворюється безліч витягнутих прямокутників з коефіцієнтом пропорційності 16 і 36, відповідно.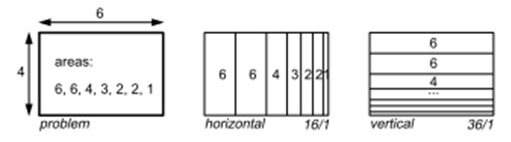

Малюнок 7 – Результат роботи алгоритму «горизонталь-вертикаль»

Першим кроком алгоритму є розбиття початкового прямокутника. Вибирається горизонтальне розбиття, оскільки ширина більше висоти. Потім, на карту додається один прямокутник (мал.7). Коефіцієнт пропорційності першого прямокутника 8 \ 3. Потім, ми додаємо другий прямокутник над першим. Коефіцієнт пропорційності поліпшується до 3 \ 2. Додаємо третій прямокутник, проте коефіцієнт пропорційності погіршується до 4 \ 1. Тому, ми вважаємо, що ми знайшли оптимальне рішення лівої половини на кроці 2 і переходимо до розбиття правої половини.

В якості початкового розбиття було вибрано вертикальне, оскільки ширина більше висоти. На кроці 4, якщо ми додамо прямокутник з площею 4, а потім з площею 3 на кроці 5, коефіцієнт пропорційності поліпшується. Додавання наступного прямокутника з площею 2 не покращує результат, тому ми вважаємо результат на 5 кроці оптимальним і переходимо до розбиття правого верхнього прямокутника.

Процес повторюється до тих пір, поки всі прямокутники не будуть розміщені. Результат квадратичного алгоритму розбивки показаний на мал.7

Малюнок 8 – Результат роботи квадратичного алгоритму розбивки

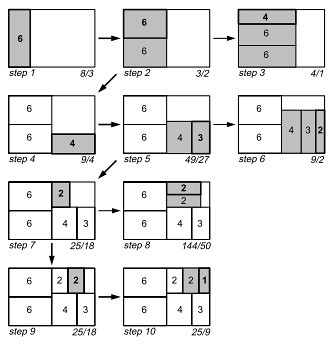
Слід сказати, що не гарантується здобуття оптимального рішення і можна придумати контрприклади. Також, важлива послідовність розміщення прямокутників. Як правило, починати краще з найбільш великих прямокутників, так як розташувати їх складніше всього.

Недоліки, властиві квадратичним і кластерним деревовидним картками:

- Невелика зміна даних призводить до значної перебудови прямокутників карти. Ці зміни відразу помітні оку, і людині дуже складно простежити динаміку зміни даних, при постійній зміні розмітки (структури) карти;

- Дані алгоритми не зберігають впорядкованість даних і, отже, легкість для читання даних алгоритмів теж дуже низька.

Оцінка складності алгоритму:

Спочатку прямокутники сортуються за розміром, що займає час O (n * logn). Час виконання решти алгоритму залежить від середньої кількості прямокутників у кожному рядку. Так як розміри прямокутника в поточному рядку повинні перераховуватися кожного разу при додаванні нового прямокутника до рядка час виконання виходить O (n * logn) + O (n * B (n)), де B (n) – середня кількість прямокутників у рядку. Таким чином, час виконання обмежено знизу O (n * logn) у разі, якщо O (B (n)) <= O (n * logn). У найгіршому випадку, коли всі прямокутники знаходяться в одній лінії (B (n) = n), час виконання буде O (n * n), яке є верхньою межею часу виконання. У середньому, проте, кожен рядок буде містити vn прямокутників і середній час виконання O (n * vn).

3.3 Впорядковані деревоподібні картки

Головною рисою даного алгоритму є те, що можливо створити таку розмітку простору карти, при якій дані наступні один за одним будуть розташовані поруч на карті. Незважаючи на те, що отримувана розмітка не слід простої лінійної послідовності, як для алгоритму «горизонталь-вертикаль», вона створює обмеження і внаслідок цього карта перебудовується трохи при змінах в даних [6].

Для алгоритмів з даного класу притаманна часткова впорядкованість елементів.

В основі впорядкованих карт, що починається від прямокутника R, який необхідно розділити. Вхідними даними є список елементів, впорядкованих за індексом і мають різні розміри. Певний елемент (опорний – pivot) вибирається та розміщується на початковому прямокутнику R, як квадрат (коефіцієнт пропорційності дорівнює 1). Решта елементи розміщуються в 3 великих прямокутниках, що утворюють невикористаний простір прямокутника R. Далі алгоритм рекурсивно застосовується до кожного з цих 3 прямокутників.

Існують наступні алгоритми впорядкованих деревовидних карт:

- опорний елемент у центрі (pivot by middle);

- опорний елемент за розміром (pivot by size);

- опорний елемент за розділеним розміром (pivot by split size).

Для алгоритму «опорний елемент за розміром» в якості опорного елемента вибирається елемент найбільшого розміру, бо, зазвичай, чим більше елемент, тим його складніше розмістити, тому, краще з нього почати, коли вся карта вільна. Ідея алгоритму показана на мал.8.

Малюнок 9 – Впорядковані деревоподібні картки

Алгоритм:

1. Вибрати опорний елемент P, найбільший за розміром.

2. Якщо ширина початкового прямокутника R більше або дорівнює висоті, розділити R на 4 прямокутника R1, Rp, R2 і R3, як показано на мал.(Інакше, якщо ширина менше висоти, поміняти осі, y = x);

3. Розташувати P у прямокутнику Rp, точні розміри якого будуть визначені на кроці 4.

4. Розділити всі елементи списку крім P по 3 групам L1, L2 і L3, щоб додати до прямокутник R1, R2 і R3. L1 і L3 можуть бути порожніми. Покладемо, що група L1 складається з елементів з індексом менше ніж P. Покладемо, що в групі L2 для всіх елементів індекс менше, ніж у групі L3 і коефіцієнт пропорційності P якомога ближче до 1.

5. Рекурсивно розміщуємо L1, L2 і L3 (якщо вони не порожні) по прямокутниках R1, R2, R3 відповідно до алгоритму.

Алгоритм «опорний в центрі» практично ідентичний розглянутому вище, різниця полягає в тому, що в якості опорного елемента вибирається не найбільший елемент, а просто центральний елемент (тобто, якщо послідовність складається з n елементів як опорного буде обраний елемент з індексом n / 2) [7].

Для алгоритму «опорний елемент за розділеним розміром» опорний елемент вибирається так, щоб загальна площа прямокутників, що розміщуються в областях R1 і R3, була приблизно однаковою.

Деревоподібні карти, отримані в результаті роботи алгоритмів «опорний елемент в центрі», «опорний елемент за розміром» і «опорний елемент за розділеним розміром» показані на мал.9.

Малюнок 10 – Порівняння упорядкованих деревовидних карток

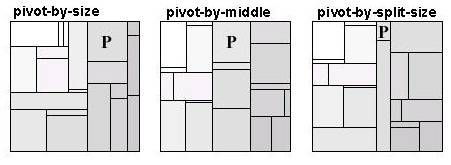
Впорядковані деревоподібні карти займають проміжне положення, середній коефіцієнт пропорційності прямокутників, що складають карту набагато нижче, ніж при традиційному алгоритмі «горизонталь-вертикаль», але не такий низький як для кластерних і квадратичних деревовидних карт. Вони змінюються значно більш плавно, ніж кластерні і квадратичні карти, але не так плавно як традиційні карти, в основі яких лежить алгоритм «горизонталь-вертикаль». Таким чином, впорядковані деревоподібні карти є гарним вибором, коли коефіцієнти пропорційності, динамічної зміни і легкість для читання, всі є важливими вимогами.

Оцінка ефективності алгоритмів:

Для алгоритмів «опорний елемент за розміром» і «опорний елемент за розділеним розміром» - O (n * logn) – в середньому і O (n * n) в гіршому випадку.

Алгоритм «опорний елемент в центрі» - O (n * logn) – в гіршому випадку.

3.4 Cмуговий алгоритм

Алгоритм «поділ по смугах» є модифікацією існуючого алгоритму квадратичних деревовидних карт. У його основі лежить упорядкована обробка послідовності прямокутників і розміщення їх в смуги (вертикальні або горизонтальні) різної ширини (Мал. 10).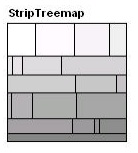

Малюнок 11 – Алгоритм поділ по смугах

Даний алгоритм переглядає та динамічно змінює ширину тільки поточної смуги прямокутників. Він забезпечує кращу легкість для читання, ніж традиційні алгоритми, що лежать в основі впорядкованих деревовидних карт і зіставні коефіцієнти пропорційності і динамічної зміни [8].

Алгоритм:

Вхідними даними є початкова область R для поділу і послідовність дочірніх прямокутників певного розміру, впорядкованих за індексом. Ми продовжуємо додавати прямокутники в поточну лінію до тих пір, поки середній коефіцієнт пропорційності всіх прямокутників даної лінії зменшується. При його збільшенні починаємо нову лінію. Кожного разу, при додаванні нового прямокутника в лінію, розміри всіх прямокутників даної лінії динамічно перераховуються, і змінюється її товщина.

Кроки алгоритму:

- отмасштабіровать загальну площу всіх прямокутників, щоб вона дорівнювала площі початкового прямокутника.

- Створити нову лінію – поточна лінія.

- Додати наступний прямокутник в поточну лінію, перерахувати товщину лінії на основі всіх прямокутників лінії, потім перерахунок ширини кожного прямокутника лінії.

- Якщо середній коефіцієнт пропорційності поточної лінії збільшився, при додаванні прямокутника на кроці 3, видалити даний прямокутник з лінії, перемістити його назад до списку прямокутників для обробки і перейти на крок 2.

- Якщо всі прямокутники оброблені – кінець, інакше – на крок 3.

Цей алгоритм є спрощеною версією квадратичного алгоритму розбивки. У квадратичному алгоритмі прямокутники сортуються за розміром, що покращує коефіцієнт пропорційності, але втрачається впорядкованість елементів. Також для квадратичного, на відміну від смугового, алгоритму прямокутники додаються як горизонтально, так і вертикально, що знову ж таки покращує коефіцієнт пропорційності, але погіршує читабельність.

Алгоритм поділу по смугах працює добре, але часто виникає проблема з розміщенням останньої лінії, так як рішення про додавання прямокутника в лінію базується тільки на середньому коефіцієнті прямокутників поточної лінії. Тому, можливо, отримання довжиною тонкої лінії в самому кінці і залишилися прямокутниках, які, в результаті, будуть дуже витягнуті.

Дана проблема може бути вирішена, якщо додати прогнозування та обробку наступної лінії наперед. Після обробки поточної лінії, вважається така лінія, і порівнюються коефіцієнти пропорційності, якщо прямокутники з наступної лінії будуть переміщені в поточну лінію. Якщо середній коефіцієнт пропорційності 2-х ліній нижче при переміщенні прямокутників з наступної лінії в поточну, вони переміщаються.

Оцінка ефективності алгоритму:

Для кожного прямокутника обчислюється середній коефіцієнт пропорційності поточного рядка. У кожному рядку, в середньому, vn прямокутників. Тому, середній час виконання - O (vn).

3.5 Квантові деревоподібні картки

Всі вище перераховані алгоритми для передачі інформації використовують такі засоби:

- розмір прямокутників;

- колір прямокутників;

- анотації.

Квантові деревоподібні карти використовують ще один шлях для передачі інформації: прямокутники карти містять візуальну інформацію, таку як фотографії або картинки [8]. Приклад квантової деревоподібної карти показаний на мал.11.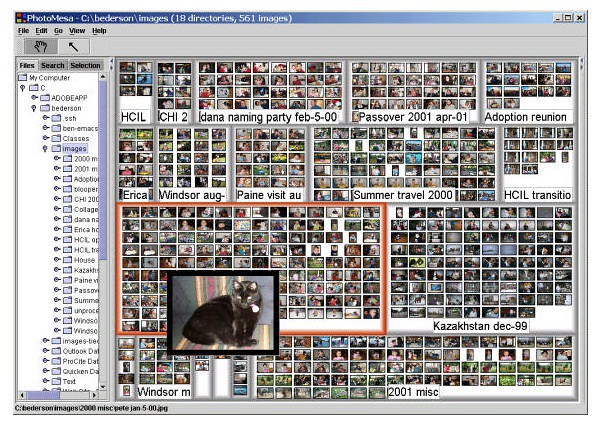

Малюнок 12 – Квантова деревоподібна карта

Проблема використання традиційних алгоритмів для відображення візуальної інформації полягає в тому, що, як правило, картинки мають фіксований розмір, в той час як більшість алгоритмів, створює деревоподібні карти з прямокутниками, розмір яких динамічно змінюється. Тому вони не підходять для відображення такого виду інформації. Рішенням даної проблеми може бути масштабування картинки в прямокутнику, але при такому підході простір карти використовується неефективно – виникає безліч порожніх областей. Приклад деревовидних карт, з використанням алгоритмів упорядкованих і квантових деревовидних карт зображений на мал.12.

Малюнок 13 - Упорядкована і квантова деревоподібна картки

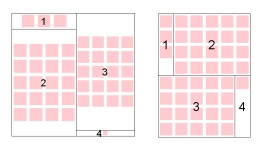
Вільне місце все одно виникає, але при застосуванні квантових деревовидних карт його на порядок менше.

4 Висновки. Цілі і завдання подальшого дослідження

Перспективними напрямками розвитку деревовидних карт є:

- оптимізація упорядкованих деревовидних карт, поліпшення коефіцієнта пропорційності;

- оптимізація кластерних і квадратичних деревовидних карт, поліпшення коефіцієнта динамічної зміни;

- дослідження можливостей компонування алгоритмів для об'єднання їх сильних сторін: глобальна стабільність – локальна удобочитаемость;

- формулювання теореми, що характеризує залежність коефіцієнта пропорційності і коефіцієнта динамічної зміни. Їм притаманна зворотна залежність;

- дослідження 3-хмерних деревовидних карт;

- знаходження нових шляхів передачі інформації: анімація, текстури, звук, лінії, картинки та інші перцепційне методи.

Головні завдання даної роботи:

- визначити області застосування деревовидних карт;

- оцінити ефективність деревовидних карт, як методу геовізуалізаціі, для відображення просторово-часових і абстрактних даних;

- розробити більш ефективні методи розбиття простору деревоподібної карти.

5 Література

1. Dodge M., McDerby M., Turner M. Geographic visualization. Concepts, tools and applications, 2008.-p. 1-9.
2. Slingsby A., Dykes J., Wood J. Using treemaps for variable selection in spatio-temporal visualization, 2008.-p. 1
3. Shneiderman B. Treemaps for space-constrained visualization of hierarchies, 1998-2009 .- p. 1-10.
4. Bruls M., Huizing K., Jarke J. Squarified treemaps, 2000. - P. 3.
5. Kerwin T., Survey of treemap techniques, 2001.
6. Shneiderman B., Wattenberg M., Ordered Treemap Layouts, 2000.
7. Engdahl B., Ordered and Unordered Treemap Algorithms and Their Applications on handheld devices, 2005.
8. Bederson B., Ordered and Quantum Treemaps: Making Effective Use of 2D Space to Display Hierarchies, 2002.
9. Lu H., Fogarty J., Cascaded Treemaps: Examining the Visibility and Stability of Structure in Treemaps, 1999.
10. Slingsby A., Using treemaps for variable selection in spatio-temporal visualisation, 2008.

Важливе зауваження

При написанні даного автореферату магістерська робота ще не завершена. Остаточне завершення: грудень 2011 Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.