Реферат по теме выпускной работы

1 Введение

2 Анализ задачи разбиения пространства с использованием древовидных карт

   2.1 Древовидные карты, как метод отображения информации

   2.2 Параметры для оценки эффективности разбиения пространства древовидной карты

3 Обзор существующих алгоритмов разбиения пространства с использованием древовидных карт

   3.1 Алгоритм «горизонталь-вертикаль»

   3.2 Квадратичные древовидные карты

   3.3 Упорядоченные древовидные карты

   3.4 Полосный алгоритм

   3.5 Квантовые древовидные карты

4 Выводы. Цели и задачи дальнейшего исследования

5 Литература

1 Введение

Исследование зависимостей и закономерностей в геоинформационных данных является сложной задачей из-за их огромного размера. Данные могут быть различной природы и из различных источников. Необходимо разработать методы эффективного взаимодействия компьютера и электронной обработки, и человеческого зрения, методы анализа и визуализации данных, стимулирующие обнаружение зависимостей, выработку гипотез и извлечение знаний из данных.

Геовизуализация – метод исследования пространственных знаний, скрытых в многомерных географических и временных данных через взаимодействие с картой и графом. Геовизуализация это не просто пассивный процесс просмотра и чтения карт. Это активный процесс, включающий сортировку, выделение, фильтрацию и преобразование данных для определения зависимостей и отношений. Карты и графики в этом контексте делают больше, чем «отображают данные», они являются активными инструментами в процессе мышления пользователя [1].

Подходы к геовизуализации

Традиционным подходом, применяющимся при геовизуализации, является прямое отображение каждой записи из массива данных; после этого аналитик изучает эти данные и старается определить какие-то зависимости. Однако множество источников и размер данных растут с каждым днем, что значительно усложняет задачу аналитика. Представление данных (на бумаге, мониторе или другом устройстве) может стать неразборчивым из-за визуальной перегруженности, больших объемов данных и информации различной природы. У пользователя могут возникнуть проблемы с восприятием, отслеживанием и пониманием множества визуальных элементов, которые изменяются параллельно. Множество методов было разработано для визуального анализа пространственных данных путем прямого отображения. Однако, маловероятно, что данные методы смогут эффективно решить проблему перегруженности изображения данными. Подходы, применяющиеся при геовизуализации больших объемов данных:

- отображение и визуализация абстрактного набора данных, полученного в результате предварительной обработки данных;

- разработка различного рода представлений для использования пространства карты более эффективно.

Среди основных методов предварительной обработки данных можно выделить:

- построение корреляционной матрицы и определение значимых факторов;

- очистка и преобразование данных;

- факторный анализ, анализ главных компонент;

- сортировка, агрегация, фильтрация и.т.д.

К методам, использующим пространство карты более эффективно, относят:

- карты плотности;

- гистограммы, диаграммы, графики, временные ряды;

- анимация;

- пространственно-временной куб;

- кольцевые карты, древовидные карты, и.т.д.

В общем виде процесс геовизуализации показан на рис. 1: основание пирамиды это сырые данные о предметной области, из-за их огромного размера их очень сложно анализировать и работать с ними. Верхушка пирамиды это данные полученные после геовизуализации: их на порядок меньше и внимание пользователя концентрируется на самом важном для принятия решения.

Рисунок 1 – Процесс геовизуализации

В данной работе будут рассмотрены древовидные карты, их эффективность при отображении больших объемов данных и области применения.

Актуальность работы:

Древовидные карты используются для отображения широкого спектра данных иерархической природы. NewsMap – онлайн приложение, которое отображает новости Google в виде древовидной карты. Цвет прямоугольника определяет тип новости, а его размер – количество статей в интернете по данной теме. Еще одним очень хорошим примером использования древовидных карт является «Карта рынка» на сайте Smartmoney.com. В этом приложении, компании разделены по разным регионам, в зависимости от сектора рынка, в котором они находятся. Размер каждого прямоугольника, характеризующего компанию, зависит от ее доли на рынке. Цвет прямоугольников также несет в себе информацию, и находится в пределах от красного до зеленого, он отвечает за динамику роста или упадка той или иной компании или сферы рынка в целом. Также существует множество приложений использующих древовидные карты для:

- отображение файловой системы;

- отображение фотографий;

- медицина, отображение генома человека;

- преобразование данных из формата Ecxel в древовидную карту;

2 Анализ задачи разбиения пространства с использованием древовидных карт

Древовидные карта - метод отображения иерархических данных больших размеров. Они эффективно совмещают в себе диаграмму Венна и секторную диаграмму. Первоначально разработанные для отображения файлов жесткого диска, сейчас древовидные карты применяются во многих отраслях, начиная от финансового анализа и заканчивая спортивными обзорами и медициной [2].

2.1 Древовидные карты, как метод отображения информации

Бен Шнидерман придумал новое представление данных в виде древовидной карты для более наглядного отображения файловой системы своего компьютера. Традиционный подход для отображения древовидных структур показывает узлы и уровни иерархии в виде папок и соединяющих стрелок (рис. 1). Это работает, и довольно хорошо, для древовидных структур малого размера. Однако, если этот же подход применяется для деревьев большего размера, с сотнями и тысячами узлов и многими уровнями иерархии, на экране появляется хаос в виде множества папок и линий.

В начале, древовидная карта состоит из одного большого прямоугольника, и затем происходит разделение этой прямоугольника на области меньшего размера рекурсивно. Начальный прямоугольник представляет корень дерева. Он разделяется на совокупность прямоугольников меньшего размера, разделенных горизонтально, каждый из которых является дочерним по отношению к корню дерева. Далее процесс повторяется, на каждом уровне иерархии направление разделения меняется с горизонтального на вертикальное, и наоборот [5].

Рисунок 2 – Традиционное отображение данных древовидной структуры

На рис. 2 показано преобразование данных, представленных в виде дерева в древовидную карту.

Рисунок 3 – Преобразование данных: дерево в древовидную карту

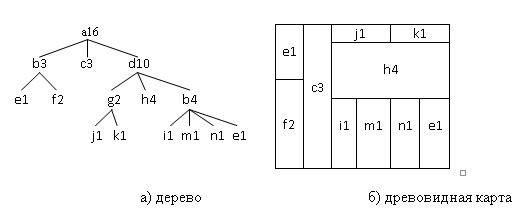
На данный момент в древовидных картах используются следующие подходы для передачи информации:

- размер прямоугольников;

- цвет прямоугольников;

- аннотации.

Отображение деревьев в виде древовидной карты имеет 2 преимущества. Первое – это то, что очень легко видеть иерархическую структуру, показаны связи между уровнями. Дочерние уровни находятся внутри своего родителя. Следующим преимуществом является то, что при таком представлении пространство карты используется очень эффективно. Начальный прямоугольник полностью заполняется прямоугольниками меньшего размера.

Древовидная карта является, особенно, эффективным средством отображения деревьев, если каждый лист дерева имеет вес, ассоциированный с ним. В качестве веса может выступать: размер файла, в случае Шнидермана, физический вес, денежная стоимость, содержание сахара и.т.д. В зависимости от веса того или иного листа, он будет занимать большее или меньшее пространство на карте [3].

2.2 Параметры для оценки эффективности разбиения пространства древовидной карты

Ключевым аспектом при создании древовидных карт является алгоритм, применяющийся для создания вложенных прямоугольников, составляющих карту. Эффективность алгоритма определяется следующими параметрами:

- среднее соотношение сторон прямоугольников (средний коэффициент пропорциональности);

- динамический коэффициент изменения;

- удобочитаемость карты;

- упорядоченность данных.

Средний коэффициент пропорциональности определяется по формуле:

- AAR (Average Aspect Ratio) – средний коэффициент пропорциональности;

- l – ширина прямоугольника;

- h – высота прямоугольника;

- n – общее количество прямоугольников.

Чем ближе коэффициент пропорциональности отдельного прямоугольника к 1, тем он ближе по форме к квадрату. И, соответственно, чем ближе средний коэффициент пропорциональности к 1, тем более «квадратной» является карта. Человеку сложно работать с вытянутыми прямоугольниками: прямоугольники с различными коэффициентами пропорциональности сложно сравнивать между собой, добавлять аннотации к ним и даже просто увидеть на карте.

Средний динамический коэффициент изменения определяется по формуле:

- ADCH (Average Dynamic Coefficient of Change) - средний динамический коэффициент изменения;

- n – общее количество прямоугольников;

- R – прямоугольник, определяется 4-мя числами(x, y, w, h);

- d(R1,R2) – расстояние между прямоугольниками, определяется по формуле:

- x1, y1 – координаты верхнего левого угла 1-го прямоугольника;

- w1, h1 – координаты нижнего правого угла 1-го прямоугольника;

- x2, y2 – координаты верхнего левого угла 2-го прямоугольника;

- w2, h2 – координаты нижнего правого угла 2-го прямоугольника .

Динамический коэффициент изменения характеризует насколько структура прямоугольников одной карты, отличается от другой. И, следовательно, чем данный коэффициент ниже, тем лучше: маленькие изменения в данных приводят лишь к небольшим перестроениям карты.

Выбираются «невзвешенные» средний коэффициент пропорциональности и динамического изменения, то есть прямоугольники с маленькой площадью влияют на данные коэффициенты, точно так же как и большие. Альтернативой может быть использование «взвешенных» коэффициентов, так как прямоугольники большего размера вносят больший вклад в общее визуальное представление. Однако проблема с вытянутыми прямоугольниками более характерна прямоугольникам меньшего размера и часто приходится ухудшать коэффициент пропорциональности больших прямоугольников в пользу маленьких. Использование «взвешенных» коэффициентов приводит к образованию маленьких, вытянутых прямоугольников [10].

Еще параметром, определяющим эффективность алгоритма, является удобочитаемость карты – метрика, характеризующая насколько легко и быстро, пользователь может найти интересующий прямоугольник. Данную метрику гораздо сложнее измерить количественно. Удобочитаемость зависит от последовательности и прогнозируемости разметки карты. Последовательность позволяет человеку следовать по шаблону быстро, не перескакивая с места на место. Прогнозируемость фокусирует взгляд пользователя на том регионе, где, по его мнению, данный прямоугольник расположен. Для количественного измерения данной метрики применяют следующие подходы:

- проведение эксперимента: показ пользователям одних и тех же данных, сгруппированных различным образом (по различным алгоритмам) и выполнение соответствующих задач по поиску нужного прямоугольника. Удобочитаемость, затем, может быть измерена посредством интервью и анализа времени поиска;

- Слежение за движением человеческого глаза во время просмотра карты. Чем чаще человек изменяет направление просмотра карты или перескакивает с места на место, тем удобочитаемость хуже. Данный подход является более механическим, и не требует дальнейших интервью после просмотра карты.

Каждой карте присваивается числовое значение, характеризующее удобочитаемость и показывающее насколько легко пользователь может найти интересующий прямоугольник.

Древовидные карты могут быть упорядоченные и неупорядоченные. Для большинства реальных данных порядок важен и он несет в себе важную часть информации, поэтому еще одним важным свойством, определяющим эффективность карты, является упорядоченность данных.

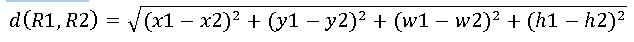
3 Обзор существующих алгоритмов разбиения пространства с использованием древовидных карт

Ключевым моментом, местом, в котором отличается, большинство алгоритмов, является рассчет границ прямоугольников. В основе большинства алгоритмов лежит последовательный шаблон – обрабатывается только один узел на каждом шаге. Существуют алгоритмы, которые просматривают наперед список дочерних узлов и их размещение, при определении границ отдельного прямоугольника. Однако главная идея всех алгоритмов остается одинаковой: функция, которая обрабатывает каждый узел, в зависимости от его размеров, выделят каждому узлу некоторое пространство. Если узел содержит дочерние узлы – они размещаются внутри родителя.

Наиболее широко-используемыми алгоритмами разбиения пространства древовидной карты являются следующие:

- традиционный алгоритм «горизонталь-вертикаль» (slice-and-dice);

- квадратичный алгоритм (squarified);

- кластер (cluster);

- опорный элемент в центре (pivot-by-middle);

- опорный элемент по размеру (pivot-by-size);

- опорный элемент по разделенному размеру (pivot-by-split-size);

- разделение по полосам (strip treemap).

3.1 Алгоритм «горизонталь-вертикаль»

Наиболее первым алгоритмом, предложенным Б. Шнидерманом, был традиционный алгоритм «горизонталь-вертикаль». Пространство карты разбивается на вложенные прямоугольники, на каждом уровне иерархии ориентация линий (горизонтальная или вертикальная) изменяется. Пример преобразования дерева и отображение его в виде древовидной карты, используя алгоритм «горизонталь-вертикаль» показан на рис. 4.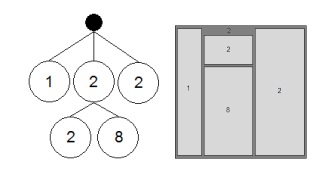

Рисунок 5 – Преобразование дерева в древовидную карту, алгоритм «горизонталь-вертикаль»

Данный алгоритм легко реализовать и он является довольно эффективным для малого размера данных, однако с увеличением размера данных данный алгоритм очень часто приводит к образованию большого количества вытянутых прямоугольников. Данная проблема показана на рис.5 – очень большое количество вытянутых прямоугольников, с которыми сложно работать [9].

Рисунок 6 – Алгоритм «горизонталь-вертикаль»

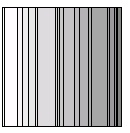
Сильными сторонами данного алгоритма являются характеристики «коэффициент динамического изменения» и «удобочитаемость». Он также сохраняет упорядоченность элементов. Однако из-за очень высокого коэффициента пропорциональности он очень редко используется на практике в чистом виде, гораздо чаще он служит мерой сравнения для других алгоритмов.

Оценка сложности алгоритма:

Древовидная карта может быть построена за один проход алгоритма по дереву. Поэтому, полагая, что вычисление размера и цвета прямоугольника неизменно, время выполнения O(n), где n – количество узлов в дереве.

3.2 Квадратичные древовидные карты

Как можно разбить начальную область на вложенные прямоугольники меньшего размера, так чтобы средний коэффициент пропорциональности был как можно ближе к 1? Список всех возможных размещений очень велик и данная проблема принадлежит к классу NP-сложных задач. Однако, в основе работы алгоритма квадратичной карты, лежит не полный перебор, не нужно находить оптимальное решение, необходимо получить хорошее решение за короткое вычислительное время [4].

В основе алгоритма квадратичной древовидной карты лежит:

- разбиение для всех подуровней не производится одновременно. Это приводит к значительному увеличению вычислительного времени. Вместо этого, на каждом уровне рассматриваются только ближайшие дочерние узлы, и производится их размещение, чтобы среднее соотношение сторон для данного уровня было близко к 1. На следующем уровне иерархии, начальным будет прямоугольник с коэффициентом пропорциональности близким к 1 и, следовательно, хорошей отправной точкой для размещения своих дочерних узлов. Затем процесс повторяется рекурсивно;

- прямоугольники размещаются вдоль линии на свободном месте до тех пор, пока наихудший (самый высокий) коэффициент пропорциональности всех прямоугольников в данной линии продолжает уменьшаться. Как только наихудший коэффициент пропорциональности достигает своего минимума, и добавление еще одного прямоугольника приводит к увеличению наихудшего коэффициента пропорциональности, размещение данной линии закончено, переходим к следующей.

Пример:

Предположим, у нас есть прямоугольник с шириной 6 и высотой 4, и данный прямоугольник необходимо разделить на меньшие прямоугольники площадью 6, 6, 4, 3, 2, 2 и 1. Результат работы традиционного алгоритма «горизонталь-вертикаль» показан на рис. 6, образуется множество вытянутых прямоугольников с коэффициентом пропорциональности 16 и 36, соответственно.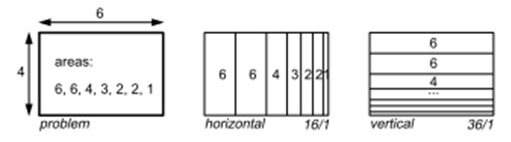

Рисунок 7 – Результат работы алгоритма «горизонталь-вертикаль»

Первым шагом алгоритма является разбиение начального прямоугольника. Выбирается горизонтальное разбиение, так как ширина больше высоты. Затем, на карту добавляется один прямоугольник (рис. 6). Коэффициент пропорциональности первого прямоугольника 8\3. Затем, мы добавляем второй прямоугольник над первым. Коэффициент пропорциональности улучшается до 3\2. Добавляем третий прямоугольник, однако коэффициент пропорциональности ухудшается до 4\1. Поэтому, мы считаем, что мы нашли оптимальное решение левой половины на шаге 2 и переходим к разбиению правой половины.

В качестве начального разбиения было выбрано вертикальное, так как ширина больше высоты. На шаге 4, если мы добавим прямоугольник с площадью 4, а затем с площадью 3 на шаге 5, коэффициент пропорциональности улучшается. Добавление следующего прямоугольника с площадью 2 не улучшает результат, поэтому мы считаем результат на 5 шаге оптимальным и переходим к разбиению правого верхнего прямоугольника.

Процесс повторяется до тех пор, пока все прямоугольники не будут размещены. Результат квадратичного алгоритма разбиения показан на рис.7

Рисунок 8 – Результат работы квадратичного алгоритма разбиения

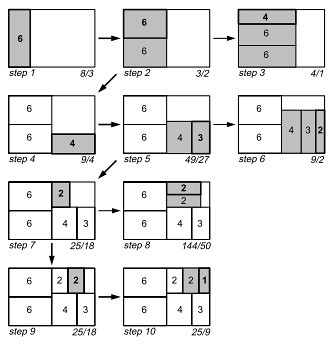
Следует сказать, что не гарантируется получение оптимального решения и можно придумать контрпримеры. Также, важна последовательность размещения прямоугольников. Как правило, начинать лучше с наиболее больших прямоугольников, так как расположить их сложнее всего.

Недостатки, присущие квадратичным и кластерным древовидным картам:

- Малейшее изменение данных приводит к значительной перестройке прямоугольников карты. Эти изменения сразу заметны глазу, и человеку очень сложно проследить динамику изменения данных, при постоянном изменении разметки (структуры) карт;

- Данные алгоритмы не сохраняют упорядоченность данных и, следовательно, удобочитаемость данных алгоритмов тоже очень низкая.

Оценка сложности алгоритма:

Вначале прямоугольники сортируются по размеру, что занимает время O(n*logn). Время выполнения оставшейся части алгоритма зависит от среднего количества прямоугольников в каждой строке. Так как размеры прямоугольника в текущей строке должны пересчитываться каждый раз при добавлении нового прямоугольника к строке время выполнения получается O(n*logn) + O(n*B(n)), где B(n) – среднее количество прямоугольников в строке. Таким образом, время выполнения ограничено снизу O(n*logn) в случае, если O(B(n))<=O(n*logn). В наихудшем случае, когда все прямоугольники находятся в одной линии (B(n)=n), время выполнения будет O(n*n), которое является верхней границей времени выполнения. В среднем, однако, каждая строка будет содержать vn прямоугольников и среднее время выполнения O(n*vn).

3.3 Упорядоченные древовидные карты

Главной чертой данного алгоритма является то, что возможно создать такую разметку пространства карты, при которой данные следующие друг за другом будут расположены рядом на карте. Несмотря на то, что получаемая разметка не следует простой линейной последовательности, как для алгоритма «горизонталь-вертикаль», она создает ограничения и вследствие этого карта перестраивается незначительно при изменениях в данных [6].

Для алгоритмов из данного класса присуща частичная упорядоченность элементов.

В основе упорядоченных карт, начинающийся от прямоугольника R, который необходимо разделить. Входными данными являются список элементов, упорядоченных по индексу и имеющих различные размеры. Определенный элемент (опорный - pivot) выбирается и размещается на начальном прямоугольнике R, как квадрат (коэффициент пропорциональности равен 1). Оставшиеся элементы размещаются в 3 больших прямоугольниках, образующих неиспользованное пространство прямоугольника R. Далее алгоритм рекурсивно применяется к каждому из этих 3 прямоугольников.

Существуют следующие алгоритмы упорядоченных древовидных карт:

- опорный элемент в центре (pivot by middle);

- опорный элемент по размеру (pivot by size);

- опорный элемент по разделенному размеру (pivot by split size).

Для алгоритма «опорный элемент по размеру» в качестве опорного элемента выбирается элемент наибольшего размера, так как, обычно, чем больше элемент, тем его сложнее разместить, поэтому, лучше с него начать, когда вся карта свободна. Идея алгоритма показана на рис. 8.

Рисунок 9 – Упорядоченные древовидные карты

Алгоритм:

1. Выбрать опорный элемент P, наибольший по размеру.

2. Если ширина начального прямоугольника R больше или равна высоте, разделить R на 4 прямоугольника R1, Rp, R2 и R3, как показано на рис. (Иначе, если ширина меньше высоты, поменять оси, y=x );

3. Расположить P в прямоугольнике Rp, точные размеры которого будут определены на шаге 4.

4. Разделить все элементы списка кроме P по 3 группам L1, L2 и L3, для добавления в прямоугольник R1, R2 и R3. L1 и L3 могут быть пустыми. Положим, что группа L1 состоит из элементов с индексом меньше чем P. Положим, что в группе L2 для всех элементов индекс меньше, чем в группе L3 и коэффициент пропорциональности P как можно ближе к 1.

5. Рекурсивно размещаем L1, L2 и L3 (если они не пустые) по прямоугольникам R1, R2, R3 в соответствии с алгоритмом.

Алгоритм «опорный в центре» практически идентичен рассмотренному выше, разница заключается в том, что в качестве опорного элемента выбирается не наибольший элемент, а просто центральный элемент (то есть, если последовательность состоит из n элементов в качестве опорного будет выбран элемент с индексом n/2) [7].

Для алгоритма «опорный элемент по разделенному размеру» опорный элемент выбирается так, чтобы общая площадь прямоугольников, размещаемых в областях R1 и R3, была примерно одинаковой.

Древовидные карты, полученные в результате работы алгоритмов «опорный элемент в центре», «опорный элемент по размеру» и «опорный элемент по разделенному размеру» показаны на рис. 9.

Рисунок 10 – Сравнение упорядоченных древовидных карт

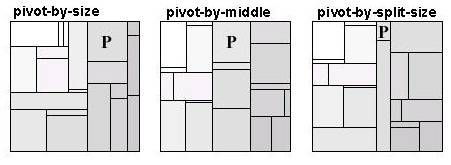
Упорядоченные древовидные карты занимают промежуточное положение, средний коэффициент пропорциональности прямоугольников, составляющих карту гораздо ниже, чем при традиционном алгоритме «горизонталь-вертикаль», но не такой низкий как для кластерных и квадратичных древовидных карт. Они изменяются значительно более плавно, чем кластерные и квадратичные карты, но не так плавно как традиционные карты, в основе которых лежит алгоритм «горизонталь-вертикаль». Таким образом, упорядоченные древовидные карты являются хорошим выбором, когда коэффициенты пропорциональности, динамического изменения и удобочитаемость, все являются важными требованиями.

Оценка эффективности алгоритмов:

Для алгоритмов «опорный элемент по размеру» и «опорный элемент по разделенному размеру» - O(n*logn) – в среднем и O(n*n) в худшем случае.

Алгоритм «опорный элемент в центре» - O(n*logn) – в худшем случае.

3.4 Полосный алгоритм

Алгоритм «разделение по полосам» является модификацией существующего алгоритма квадратичных древовидных карт. В его основе лежит упорядоченная обработка последовательности прямоугольников и размещение их в полосы (вертикальные или горизонтальные) различной ширины (Рис. 10).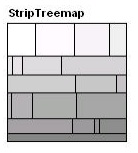

Рисунок 11 – Алгоритм разделение по полосам

Данный алгоритм просматривает и динамически изменяет ширину только текущей полосы прямоугольников. Он обеспечивает лучшую удобочитаемость, чем традиционные алгоритмы, лежащие в основе упорядоченных древовидных карт и сопоставимые коэффициенты пропорциональности и динамического изменения [8].

Алгоритм:

Входными данными является начальная область R для разделения и последовательность дочерних прямоугольников определенного размера, упорядоченных по индексу. Мы продолжаем добавлять прямоугольники в текущую линию до тех пор, пока средний коэффициент пропорциональности всех прямоугольников данной линии уменьшается. При его увеличении начинаем новую линию. Каждый раз, при добавлении нового прямоугольника в линию, размеры всех прямоугольников данной линии динамически пересчитываются, и изменяется ее толщина.

Шаги алгоритма:

- Отмасштабировать общую площадь всех прямоугольников, чтобы она равнялась площади начального прямоугольника.

- Создать новую линию – текущая линия.

- Добавить следующий прямоугольник в текущую линию, пересчитать толщину линии на основе всех прямоугольников линии, затем пересчет ширины каждого прямоугольника линии.

- Если средний коэффициент пропорциональности текущей линии увеличился, при добавлении прямоугольника на шаге 3, удалить данный прямоугольник из линии, переместить его обратно в список прямоугольников для обработки и перейти на шаг 2.

- Если все прямоугольники обработаны – конец, иначе – на шаг 3.

Данный алгоритм является упрощенной версией квадратичного алгоритма разбиения. В квадратичном алгоритме прямоугольники сортируются по размеру, что улучшает коэффициент пропорциональности, но теряется упорядоченность элементов. Также для квадратичного, в отличии от полосного, алгоритма прямоугольники добавляются как горизонтально, так и вертикально, что опять же улучшает коэффициент пропорциональности, но ухудшает удобочитаемость.

Алгоритм разделения по полосам работает хорошо, но часто возникает проблема с размещением последней линии, так как решение о добавлении прямоугольника в линию базируется только на среднем коэффициенте прямоугольников текущей линии. Поэтому, возможно, получение длиной тонкой линии в самом конце и оставшихся прямоугольниках, которые, в результате, будут очень вытянутые.

Данная проблема может быть решена, если добавить прогнозирование и обработку следующей линии наперед. После обработки текущей линии, считается следующая линия, и сравниваются коэффициенты пропорциональности, если прямоугольники из следующей линии будут перемещены в текущую линию. Если средний коэффициент пропорциональности 2-х линий ниже при перемещении прямоугольников из следующей линии в текущую, они перемещаются.

Оценка эффективности алгоритма:

Для каждого прямоугольника вычисляется средний коэффициент пропорциональности текущей строки. В каждой строке, в среднем, vn прямоугольников. Поэтому, среднее время выполнения – O(vn).

3.5 Квантовые древовидные карты

Все выше перечисленные алгоритмы для передачи информации используют следующие средства:

- размер прямоугольников;

- цвет прямоугольников;

- аннотации.

Квантовые древовидные карты используют еще один путь для передачи информации: прямоугольники карты содержат визуальную информацию, такую как фотографии или картинки [8]. Пример квантовой древовидной карты показан на рис. 11.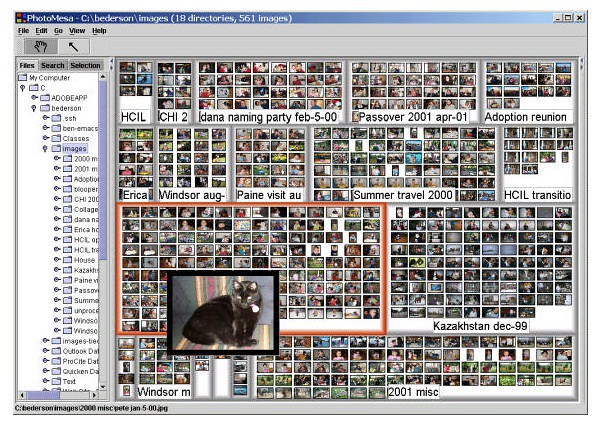

Рисунок 12 – Квантовая древовидная карта

Проблема использования традиционных алгоритмов для отображения визуальной информации состоит в том, что, как правило, картинки имеют фиксированный размер, в то время как большинство алгоритмов, создает древовидные карты с прямоугольниками, размер которых динамически изменяется. Поэтому они не подходят для отображения такого вида информации. Решением данной проблемы может быть масштабирование картинки в прямоугольнике, но при таком подходе пространство карты используется неэффективно - возникает множество пустых областей. Пример древовидных карт, с использованием алгоритмов упорядоченных и квантовых древовидных карт показан на рис. 12.

Рисунок 13 – Упорядоченная и квантовая древовидная карты

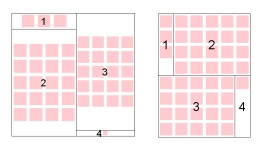
Свободное место все равно возникает, но при применении квантовых древовидных карт его на порядок меньше.

4 Выводы. Цели и задачи дальнейшего исследования

Перспективными направлениями развития древовидных карт являются:

- оптимизация упорядоченных древовидных карт, улучшение коэффициента пропорциональности;

- оптимизация кластерных и квадратичных древовидных карт, улучшение коэффициента динамического изменения;

- исследование возможностей компоновки алгоритмов для объединения их сильных сторон: глобальная стабильность – локальная удобочитаемость;

- формулировка теоремы, характеризующей зависимость коэффициента пропорциональности и коэффициента динамического изменения. Им присуща обратная зависимость;

- исследование 3-хмерных древовидных карт;

- нахождение новых путей передачи информации: анимация, текстуры, звук, линии, картинки и другие перцепционные методы.

Главные задачи данной работы:

- определить области применения древовидных карт;

- оценить эффективность древовидных карт, как метода геовизуализации, для отображения пространственно-временных и абстрактных данных;

- разработать более эффективные методы разбиения пространства древовидной карты.

5 Литература

1. Dodge M., McDerby M., Turner M. Geographic visualization. Concepts, tools and applications, 2008.-p. 1-9.
2. Slingsby A., Dykes J., Wood J. Using treemaps for variable selection in spatio-temporal visualization, 2008.-p. 1
3. Shneiderman B. Treemaps for space-constrained visualization of hierarchies, 1998-2009.- p. 1-10.
4. Bruls M., Huizing K., Jarke J. Squarified treemaps, 2000. - p. 3.
5. Kerwin T., Survey of treemap techniques, 2001.
6. Shneiderman B., Wattenberg M., Ordered Treemap Layouts, 2000.
7. Engdahl B., Ordered and Unordered Treemap Algorithms and Their Applications on handheld devices, 2005.
8. Bederson B., Ordered and Quantum Treemaps: Making Effective Use of 2D Space to Display Hierarchies, 2002.
9. Lu H., Fogarty J., Cascaded Treemaps: Examining the Visibility and Stability of Structure in Treemaps, 1999.
10. Slingsby A., Using treemaps for variable selection in spatio-temporal visualisation, 2008.

Важное замечание

При написании данного автореферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2011 г. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.