ДонНТУ   Портал магистров

Скорич Василий Игоревич

Факультет компьютерных наук и технологий

Кафедра компьютерной инженерии

Специальность «Компьютерные системы и сети»

Априорный анализ виртуальных параллельных моделей управляемого сетевого динамического объекта с распределенными параметрами

Научный руководитель: д.т.н., проф. Святный Владимир Андреевич

Резюме Биография Реферат Библиотека Ссылки Отчет о поиске Индивидуальный раздел

Реферат по теме выпускной работы

Содержание

• Введение
• 1. Актуальность темы
• 2. Цели и задачи исследований
• 3. Концепция РПМС и принцип декомпозиции на подсистемы
• 4. Анализ состояния разработок
• 5. Математическое описание сетевого динамического объекта
• 6. Уровни распараллеливания
• 6.1 Уровень 1: одно уравнение – один процесс. Минимальная гранулярность
• 6.2 Уровень 2: один элемент ветви (2 уравнения) – один процесс
• 6.3 Уровень 3: одна ветвь – один процесс
• 6.4 Уровень 4: подграф сетевого объекта – один процесс
• Выводы
• Список источников

Введение

В современном мире любая высокотехнологичная разработка требует экспериментального исследования перед своим внедрением. Но проведение натурных экспериментов обычно является трудным или экономически невыгодным. Решением данной проблемы является моделирование – изучение необходимых свойств объектов с помощью разработанных математических моделей реальных объектов.

С развитием вычислительной техники наиболее актуальным направлением стало компьютерное моделирование. Но постоянно растущая сложность объектов приводит к соответствующему росту затрат времени моделирования и мощности вычислительных ресурсов. Однопоточные системы уже не справляются с современными нагрузками задач моделирования. Следовательно, возникает необходимость разработки и внедрения многопоточных моделирующих систем.

Внедрение новых концепций моделирования привело к появлению новых проблем, а именно – необходимости создания формализованного подхода к разработке и построению сложных проблемно-ориентированных параллельных систем. Так появилась концепция распределенной параллельной моделирующей среды (РПМС).

1. Актуальность темы

Объектом, обрабатываемым в РПМС, является сетевой динамический объект с распределенными или сосредоточенными параметрами (СДОРП и СДОСП) – формальное описание, содержащее формализованное топологическое представление объекта и системы уравнений физических процессов сложной динамической системы (СДС), объединяющей их с помощью векторно-матричных выражений и операций.

Исследование и разработка такой системы является актуальным и перспективным направлением. А благодаря принципу декомпозиции разработка каждой подсистемы РПМС является относительно независимой задачей с рядом конкретных проблем.

С усложнением целевых систем для параллельного моделирования возникает проблема выбора оптимальной структуры и состава РПМС. Проведение подобной оценки на этапе разработки, девиртуализации и имплементации системы позволяет значительно сократить экономические, временные и ресурсные затраты и получить при этом наиболее производительную систему. Также важным является предвидение показателей ускорения при распараллеливании и дальнейшем наращивании системы, что позволяет сделать вывод о ее экономической эффективности. Именно такие задачи решает система априорного анализа.

2. Цели и задачи исследований

Целью работы является исследование методов и подходов к решению задачи априорного анализа виртуальных параллельных моделей управляемого сетевого динамического объекта с распределенными параметрами.

Для достижения поставленных целей необходимо решить ряд задач:

• Разработка математического описания сетевого объекта.
• Определение перечня критериев эффективности виртуальных параллельных моделей.
• Математическое описание критериев эффективности.
• Разработка системы программной поддержки априорно анализа.
• Разработка рекомендаций для девиртуализации модели.
• Проведение тестов и модельных экспериментов.

3. Концепция РПМС и принцип декомпозиции на подсистемы

Концепция РПМС для СДС с распределенными и сосредоточенными параметрами предложена в 1992 году в рамках сотрудничества Донецкого национального технического университета и Института параллельных и распределенных систем (IPVS) Штутгартского университета (Германия). Она была опубликована в докладе [1] и развита в работе [2].

Согласно [2] РПМС – это дружественная к пользователю системная организация аппаратного обеспечения, системного и целевого моделирующего программного обеспечения, которая поддерживает все этапы разработки и реализации СДОРП и СДОСП. Ключевой задачей является разработка полнофункциональной РПМС, удовлетворяющий следующим параметрам:

• Использование уже существующих SIMD и MIMD-архитектур в РПМС.
• Разработка полнофункционального программного обеспечения для моделирования SIMD и MIMD-компонентов РПМС согласно требованиям динамической системы.
• Моделирование динамических систем с сосредоточенными и распределенными параметрами на общей методической основе.
• Разработка специализированного программного обеспечения для описания параллельных процессов.
• Объектно-ориентированная реализация моделирующего программного обеспечения.
• Наличие средств для работы на всех этапах разработки СДС.
• Высокоинтеллектуальная диалоговая поддержка пользователя на всех этапах разработки и моделирования СДС.

Разработка такой полнофункциональной системы является чрезвычайно сложной задачей. Для решения этой проблемы в работе [2] отмечается целесообразность декомпозиции сложной системы РПМС на несколько подсистем. При этом разработка каждой из таких подсистем может проводиться относительно независимо от других.

Согласно предложенной концепции РПМС должна состоять из следующих подсистем:

• подсистема диалога;
• подсистема топологического анализа;
• подсистема генерации уравнений;
• подсистема виртуальных параллельных моделей;
• подсистема параллельных решателей уравнений;
• подсистема обмена данными;
• подсистема балансировки нагрузки;
• подсистема визуализации;
• подсистема баз данных;
• подсистема IT-поддержки.

Априорный анализ непосредственно взаимодействует с подсистемами виртуальных параллельных моделей, подсистемой балансировки нагрузки и обмена данными и тесно связан с процессом девиртуализации виртуальной параллельной модели.

Девиртуализация модели сложной динамической системы – это ее преобразование по методам и алгоритмам, обеспечивающее оптимальное выполнение заявки на моделирование СДС в целевой параллельной вычислительной системе.

Априорная оценка параллельной виртуальной модели на этапе девиртуализации позволяет определить оптимальные подходы к ее распараллеливанию путем рассмотрения возможных уровней распараллеливания и вариантов, которые имеют качественно лучшие показатели по равномерности загрузки процессов и по объему передачи данных.

4. Анализ состояния разработок

Задача априорного анализа появилась вместе с появлением параллельных вычислительных систем. Решению данной проблемы посвящен определенное число работ, но законченного программно-аппаратного решения не существует.

Основной работой в направлении априорного анализа виртуальных моделей является [3]. В ней подробно рассматриваются основные теоретические вопросы на базе конкретных примеров в реальных отраслях промышленности. В работе четко очерчена концепция системы и математический базис.

Так, согласно [3], главными целями априорного анализа являются:

• рассмотрение возможных подходов к распараллеливанию и структурному представлению СДОРП, начиная с минимально гранулярных процессов;
• исследование и сравнение уровней распараллеливания по критериям распределения нагрузки, обмена данными и синхронизации процессов;
• предложение и проверка возможных альтернативных решений по организации уровней распараллеливания;
• проведение общего сравнения уровней распараллеливания и формулировка рекомендаций по дальнейшей имплементации модели на целевую вычислительную систему.

Основными показателями априорного анализа являются [3]:

• равномерность загрузки виртуальных процессов. Под загрузкой в данном случае понимают количество операций, выполняемых процессом;
• соотношение между арифметическими операциями и операциями обмена данными;
• прирост ускорения вычислений при увеличении количества процессов;
• распределение процессов на реальные процессоры при имплементации модели на целевую вычислительную систему.

В литературе [3, 4] также отмечается, что априорный анализ выполняется для виртуальных параллельных моделей четырех уровней распараллеливания, приведенных на рис. 1.

Первый уровень – уровень процессов минимальной гранулярности. Определяется соотношением «одно уравнение – один процесс».

На втором уровне распараллеливания каждому процессу ставится в соответствие элемент ветви графа. Для этого уровня характерно соотношение «один элемент – один процесс».

Третий уровень – уровень распараллеливания типа «один узел – один процесс» и «одна ветвь – один процесс».

Четвертый уровень – это декомпозиция графа на подграфы, имеющие наименьшее количество связей друг с другом. В этом случае количество процессов зависит от числа подграфов, на которые разбивают СДОРП.

Следует отметить, что работы по априорному анализу параллельных моделей велись в ДонНТУ в контексте разработки отдельных подсистем РПМС, но им не уделялось специальное внимание.

Так в работе [5] отмечается, что априорный анализ виртуальной параллельной модели является неотъемлемым и важным в процессе девиртуализации виртуальной параллельной модели и ее имплементации.

Можно выделить работу [6], где отдельно выполнен априорный анализ сетевого динамического объекта с распределенными параметрами на втором уровне распараллеливания.

Следует отметить, что проблемами параллельного моделирования активно занимаются европейские институты ([7], [8], [9]).

Так, в High Performance Computing Center Stuttgart активно разрабатывается система SEGL – современный инструмент для описания и выполнения многомерных программ на распределенных высокопроизводительных вычислительных ресурсах. [10]

Также в качестве примера можно выделить работу [11], целью которой является разработка основ применения распределенных и параллельных систем моделирования. Основное внимание уделяется моделированию сложных производственных процессов, приводится обоснование эффективности таких систем в современных технологических процессах. Цель данной работы заключается в определении основных принципов достижения ускоренного выполнения моделирования за счет распараллеливания и распределения.

5. Математическое описание сетевого динамического объекта

Под сетевым динамическим объектом понимают совокупность элементов, связанных между собой физическими узлами, через которые осуществляются целенаправленные распределения потоков (электрического тока, потоков жидкостей и газов и т.п.) [4].

Сетевой динамический объект характеризуется топологией – расположением ветвей и узлов их пересечения, активных и пассивных элементов и т.д. Топология может быть представлена в виде технологических схем, графов, структур автоматизированных систем или их сочетанием.

Физические процессы, происходящие в модели, описываются с помощью системы дифференциальных уравнений в частных производных (пример приведен для управляемого сетевого динамического объекта – вентиляционной шахты):

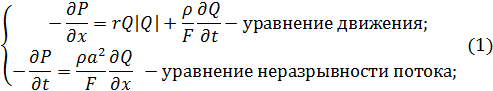
где P(x, t) – давление;

Q(x, t) – расход воздуха;

r – удельное аэродинамическое сопротивление воздухопровода;

ρ – плотность воздуха;

F – площадь сечения воздухопровода;

а – скорость звука в воздухе;

х – пространственная координата вдоль оси воздухопровода в пределах его длины.

Граничными условиями для (1) являются функции давления в начальном и конечном узлах ветви. По типу граничных условий ветви делятся на три типа [12]:

• ветви, инцидентные внутренним узлам сети, в которых давление рассчитывается в процессе решения сетевой системы уравнений в соответствии с узловыми динамическими условиями;

  

  где P_wi – давление в узле wi;

  Q_wi – общий расход воздуха через узел wi;

  F_wi – площадь поперечного сечения узла;

• ветви, инцидентные узлу подключения вентилятора; в этом узле давление задается как характеристика вентилятора

P_wj=P_FANj (3)

• ветви, инцидентные узлу выхода в атмосферу; здесь принимается постоянное давление атмосферы

P_wj=P_ATM=const (4)

Для моделирования сетевого динамического объекта (СДО) необходимо произвести его формальное описание (модель), которое включает:

• таблицу кодирования и топологические характеристики, которые могут быть получены из нее и использованы в уравнениях;
• m пар уравнений типа (1), записанных для каждой ветви СДО

• n₁ узловых граничных условий – давлений в узлах;
• n₂ характеристик вентиляторов (или других активных элементов);
• n₃ открытых выходов в атмосферу, где давления принимаются постоянными и равными атмосферному давлению.

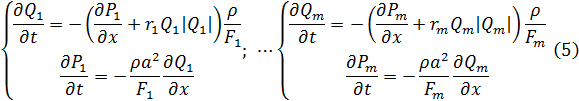
Таким образом, сетевой объект с распределенными параметрами описывается m системами уравнений (1) с n = n1 + n2 + n3 граничными условиями, где m – число ветвей графа, n₁, n₂, n₃ – количество узлов с условиями (2), (3), (4) соответственно.

Все ветви графа аппроксимируются по пространственным координатам согласно схеме, приведенной на рис. 2.

M = l_i/Δx – количество элементов, на которые разбивается ветвь;

l_i – длина ветви;

Δx – шаг.

Для k-ого элемента ветви Q_j уравнения (5) записываются в виде, удобном для применения численных методов (пространственно дискретизированная Simulation Model, ПДSM):

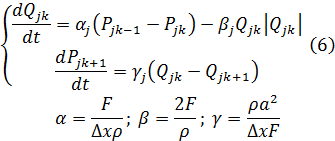
В (6) пространственная координата x рассматривается как дискретная, а время t остается непрерывным. Производная по дискретной переменной заменена разностью.

При этом для всей сети j ∈ (1, 2, … m), индекс k = 1, 2, … M_j в пределах каждой ветви, а M_j зависит от длины ветви и шага Δx аппроксимации по пространственной координате.

Граничные условия для уравнений воздушных потоков в ветвях делятся на внешние и внутренние. К внешним относятся давления в начальных узлах, чьи ветви соединены с атмосферой, и давления в узлах, к которым подключены вентиляторы. Внутренние граничные условия – это давления в узлах сети, которые должны быть вычислены при решении системы уравнений.

Внутренние граничные условия определяются в соответствии со следующим уравнением:

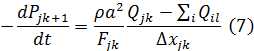
где ∑_iQ_il – алгебраическая сумма расходов в элементах ветвей, инцидентных граничному узлу,

i – номер ветви,

l = 1 (если ветвь выходит из узла), M_i (если ветвь входит в узел)

M_i – число элементов, аппроксимирующих i-ую ветвь.

В общем случае граничные условия являются переменными типа P, которые вычисляются по уравнениям неразрывности в граничных точках аппроксимации ветвей M_j+1, совпадающих с узлами сети:

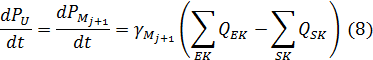
где Q_SK и Q_EK – расходы воздуха в начале и конце ветви соответственно.

На основе уравнений (6) и (7) должна генерироваться система уравнений для всей сети, аппроксимирующая систему (5).

6. Уровни распараллеливания

6.1 Уровень 1: одно уравнение – один процесс. Минимальная гранулярность

Структура виртуальной параллельной Simulation Model (ВПSM) одной ветви сетевого объекта, дискретизированной по пространственной координате M элементами, представлена на рис. 3.

Здесь Q- и P-процессы обеспечивают решение уравнений (6).

Загрузка виртуальных процессов

Загрузка определяется составом операций, необходимых для решения Q- и P-уравнений.

Из (6) видно, что правая часть Q-уравнения отличается от правой части P-уравнения наличием слагаемого β_jQ_jk|Q_jk|. Длительность выполнения операций составляет

T_Q=t_mul+t_sum+t_mod=2t_sum+3t_mul+t_mod (9)

T_P=t_mul+t_sum (10)

где t_mul, t_sum, t_mod – соответственно длительности операций умножения, алгебраического сложения и определения модуля переменной.

Время неравномерности

ΔT=T_Q–T_P=t_mod+2t_mul (11)

не зависит от выбранного численного метода и указывает на то, что Р-процессы не догружены практически в 2 раза.

Таким образом, уровню процессов минимальной гранулярности присуща неравномерность загрузки, которая приводит к потере эффективности параллельного исполнения процессов.

Соотношение между объёмами вычислительных и вспомогательных операций

Как видно на рис. 3, каждый Q-процесс имеет три входных переменных и одну выходную, а Р-процесс – две входных и одну выходную переменные. Ввиду того, что переменная Q_k, вычисляемая в k-м элементе, является переменной обратной связи (рис. 3), то отсутствует необходимость организовывать передачу Q_k с выхода на вход в Q-процессе. Таким образом, Q-процесс должен выполнить такие вспомогательные операции:

• ввод P_k из k-ого Р-процесса;
• ввод P_k+1 из k+1-ого Р-процесса;
• посылка Q_k k-ому Р-процессу;
• посылка Q_k k+1-ому Р-процессу.

В свою очередь, Р-процесс должен выполнять следующие операции:

• посылка P_k k–1-му Q-процессу;
• посылка P_k k-му Q-процессу;
• ввод Q_k-1 из k–1-ого Q-процесса;
• ввод Q_k из k-ого Q-процесса.

Таким образом, на каждом шаге вычислений Q- и Р-процессы должны выполнить по 4 операции обмена данными. По отношению к Q-процессу, где согласно (9) выполняется 6 вычислительных операций, операции обмена составляют соответственно 2/3. По отношению к Р-процессам, где число вычислительных операций соответствует формуле (10), операции обмена составляют 4/2 = 2.

В целом на 8 операций уравнений вида (6) должно выполняться по 8 операций обмена.

Схема связи между виртуальными процессами

На рис. 3 показано взаимодействие Q- и Р-процессов по их входам и выходам. Предлагаются виртуальные PQ- и QP-коммутаторы, состоящие из переключательных элементов (рис. 4).

Переменная Q_k (выход Q-процесса) дублируется и подключается на вход процессов P_k, P_k+1. Переменная P_k+1 (выход P-процесса) после удвоения подключается на вход процессов Q_k, Q_k+1.

Для минимизации времени обмена T_exch работа виртуального коммутатора должна быть организована следующим образом:

1. Схема соединений реализуется до начала решения и остаётся неизменной на весь период моделирования.
2. В i-ом цикле решения запоминаются значения компонент векторов по мере их вычисления и записываются в регистры выходов Q- и Р-процессов.
3. По завершении цикла «вычисление – запись» самым длинным процессом все процессы синхронизируются.
4. Синхронно для всех Q- и Р-процессов активируются команды посылки и получения, в один такт на входах Q- и Р-процессов появляются актуальные значения переменных и на следующем такте записываются в память.
5. Запускается i+1-ый цикл решения.

При этой организации работы коммутатора и параллельной передаче всех разрядов Q- и Р-чисел время обмена будет определяться формулой

T_exch=t_regwr+t_regrd+t_trans+t_rec+t_wr (12)

где t_regwr – время записи в регистр в самом длинном Q-процессе;

t_regrd – время считывания из регистра;

t_trans – время передачи по линии связи;

t_rec – время приёма из линии связи в регистр;

t_wr – время записи из регистра в память.

Соотношение «процесс – процессор» при отображении на виртуальную и целевую параллельные архитектур

На первом уровне требуется следующее количество процессорных элементов N_PE1 для вычисления расходов воздуха и давлений ветвей:

N_PE1=2∑^m_j=1M_j (13)

Здесь m – количество ветвей в сетевом объекте, M_j – количество элементов в ветвях. В свою очередь M_j определяется длиной ветви и шагом аппроксимации по пространственной координате Δx:

M_j=l_j/Δx (14)

Так как величина Δx для всей сети должна быть одинаковой, то число процессов определяется суммарной длиной ветвей:

N_PE1=(2/Δx)∑^m_j=1l_j (15)

Отсюда следует, что первый уровень распараллеливания требует такого количества виртуальных процессов и процессоров, которое существенно превышает технические возможности доступных пользователям MIMD-систем.

По формуле (15) можно сделать оценку возможного шага Δх и параметров M_j, которые может обеспечить целевая параллельная MIMD-система с известным числом процессоров N_TCA:

Δx_POSS=(2/N_TCA)∑^m_j=1l_j (16)

6.2 Уровень 2: один элемент ветви (2 уравнения) – один процесс

Равномерность загрузки процессов

Соотношение один элемент ветви – один процесс означает, что система уравнений (6) для k-ого элемента (1 ≤ k ≤ M_j) ветви j (1 ≤ j ≤ m) решается в соответствующем k-ом MIMD-процессе. Виртуальная параллельная модель для одной ветви показана на рис. 5.

Загрузка процессов вычислениями увеличилась, время вычисления правых частей в k-ом процессе составляет

T_QP=T_Q+T_P (17)

Для простых ветвей T_Q, T_P вычисляются по формулам (9), (10), и T_QP составит:

T_QPmin=2t_sum+t_mod+3t_mul+t_sum=3t_sum+4t_mul+t_mod (18)

Соотношение между объёмами вычислительных и вспомогательных операций

Для уровня 2 соотношение изменяется в сторону уменьшения доли операций обмена. Из рис. 5 следует, что k-ый процесс j-ой ветви (QP)_jk выполняет такие вспомогательные операции:

• ввод P_k из соседнего k–1-ого процесса;
• ввод Q_k+1 из соседнего k+1-ого процесса;
• посылка Q_k соседнему k–1-ому процессу;
• посылка P_k+1 соседнему k+1-ому процессу.

Так, на 8 операций при вычислении правой части уравнений вида (6) должно выполняться 4 операции обмена.

Таким образом, на уровне «один элемент ветви – один процесс» в два раза улучшается соотношение между объёмом вычислений и операций обмена.

Схема связи между виртуальными процессами

Схема связи следует из структуры ВПSM (рис. 5). Процесс (QP)_jk для k-ого элемента j-ой ветви имеет схему связей с соседними процессами (QP)_jk-1, (QP)_jk+1, показанную на рис. 6.

Связь между соседними процессами осуществляется коммутирующими элементами 2×2 с перекрёстным включением. На данном уровне распараллеливания легко объединяются узловые процессы P_U с любым из Q-процессов инцидентной ветви.

Соотношение «процесс – процессор» при отображении на виртуальную и целевую параллельные архитектуры

Виртуальная параллельная модель уровня 2 требует для СДОРП следующее количество виртуальных процессов:

N_PE2=∑^m_j=1M_j (19)

С учётом (14) имеем:

N_PE2=(1/Δx)∑^m_j=1l_j (20)

Это количество процессов в значительно большей степени соответствует количеству процессоров в современных MIMD-системах.

При известном количестве процессоров N_TCA имеем возможный шаг

Δx_POSS=(1/N_TCA)∑^m_j=1l_j (21)

6.3 Уровень 3: одна ветвь – один процесс

Равномерность загрузки процессов

Уровень распараллеливания «1 ветвь – 1 процесс» должен иметь m QP-процессов, решающих системы уравнений относительно переменных Q_jk, P_jk+1 j-ой ветви (k = 1, 2, …, M_j), а также n P_U-процессов, решающих узловые уравнения и дающих граничные давления в узлах для всех ветвей. Расчёты P_U могут быть совмещены с QP-процессами предузловых элементов ветвей и, следовательно, нет необходимости выделять отдельно P_U-процессы.

Загрузка процессов определяется количеством решаемых уравнений и составляет по ветвям

L_j=2M_j=2l_j/Δx (22)

Ввиду того, что ветви имеют разные длины, загрузка будет изменяться в пределах

L_min≤L_j≤L_max (23)

где L_min, L_max – соответственно загрузка по ветвям минимальной и максимальной длин.

Неравномерность длин составляет

ΔL=L_max–L_min=2(M_jmax–M_jmin) (24)

Зная время исполнения QP-процесса уровня 2, можно оценить максимальное время ожидания по всему объекту

T_Wmax=ΔL·T_QP (25)

и времена ожидания по процессам всех ветвей по отношению к процессу ветви l_max:

T_Wj=ΔL_j·T_QP (26)

где ΔL_j=L_max–L_j.

Длины выработок шахтных вентиляционных сетей имеют разброс в несколько раз. Поэтому неравномерность загрузки процессов будет весьма существенной. Предлагается модификация данного уровня распараллеливания: «1 процесс – 1 ветвь минимальной длины l_jmin». При этом количество подветвей в каждой ветви составит N_Pj=l_j/l_min.

Соотношение между объёмами вычислительных и вспомогательных операций

Соотношение улучшилось в сторону уменьшения доли вспомогательных операций. Процесс-ветвь решает 2M_j уравнений и выполняет такие вспомогательные операции:

• ввод P_j1 из узлового процесса, инцидентного начальному узлу;
• ввод расходов начальных элементов ветвей, инцидентных конечному узлу j-ой ветви;
• посылка расхода Q_j1 процессу начального узла;
• посылка вычисленного давления P_jM_j+1 в конечном узле ветви Q_j, процессам, вычисляющим расходы Q_j1 в инцидентных ветвях.

Таким образом, на 8М_j вычислительных операций уравнений вида (6) должно выполняться, аналогично второму уровню, 4 операции обмена.

На уровне 3 в варианте «1 ветвь – 1 процесс» в М_j раз улучшается соотношение между объёмом вычислений и количеством операций обмена по каждой ветви.

В варианте «1 подветвь – 1 процесс» каждой ветви соответствует N_Pj+1 процесс. Из структуры процессов следует, что каждый из них решает не менее M_min=l_jmin/Δx пар уравнений вида (6) и при этом выполняет такие вспомогательные операции:

• ввод P_jk из последнего элемента соседнего процесса;
• ввод Q_jk+h из первого элемента соседнего процесса (h ≤ M_min – шаг по числу элементов в процессах);
• вывод Q_jk из первого элемента на последний элемент соседнего процесса;
• вывод P_jk+h из последнего элемента на первый элемент соседнего процесса.

Отсюда следует, что число вспомогательных межпроцессорных операций обмена осталось равным 4. Таким образом, на 8Мmin операций по вычислению правых частей уравнений вида (6) должно выполняться 4 операции обмена.

По отношению к варианту 1 доля обменов выше, т. к. на каждую ветвь мы ввели большее число процессов в M_j/М_min раз. При этом улучшилась равномерность загрузки процессов.

Схема связи между виртуальными процессами

Из структуры процессов следует, что схемы связи между j процессами и процессами подветвей, инцидентных узлам, аналогичны. Процессы содержат M_min QP-процессов второго уровня, которые вычисляют переменные j-ой ветви от k = 1 до M_min (первый процесс), k = M_min + 1 до k = 2M_min (второй процесс) и т.д. По схеме связи последний подпроцесс QP_jM_min посылает первому подпроцессу QP_jM_min+1 соседнего процесса давление P_jM_min+1 и принимает от него расход Q_jM_min+1. Точно так же последний подпроцесс QP_j2M_min соседнего процесса посылает давление P_j2M_min+1 своему соседу и принимает от него расход Q_j2M_min+1. Если число элементов в процессах меньше M_min, то схема связи остаётся без изменений и точно соответствует схеме на рис. 6: передача давлений и расходов осуществляется через коммутирующие элементы 2×2. Их число на каждую ветвь на единицу меньше числа процессов, т.е. N_Pj – 1.

Таким образом, виртуальный коммутатор для ВПSM на третьем уровне распараллеливания строится аналогично коммутатору второго уровня на базе коммутирующих элементов 2×2.

Соотношение «процесс – процессор» при отображении на виртуальную и целевую параллельные архитектуры

Варианты 1 и 2 виртуальной параллельной модели уровня 3 требуют для СДОРП следующие количества процессов:

N⁽¹⁾_PE3=m (27)

N⁽²⁾_PE3=N_P=∑^m_j=1N_Pj+(m–m_ml) (28)

С учётом того, что N_Pj=l_j/l_min, получим

N⁽²⁾_PE3=(1/l_min)∑^m_j=1l_j+(m–m_ml) (29)

Здесь m_ml – количество ветвей с длиной lmin;

(m – m_ml) – количество дополнительных процессов в ветвях с l_j > l_min.

При отображении на виртуальные параллельные системы соотношение «1 процесс – 1 процессор» является естественным. Отображение на целевую параллельную вычислительную систему с соотношением «1 процесс – 1 процессор» возможно как по N_PE3⁽¹⁾, так и по N_PE3⁽²⁾.

6.4 Уровень 4: подграф сетевого объекта – один процесс

При таком подходе к распараллеливанию граф сетевого объекта разбивается на Gs подграфов, имеющих наименьшее количество связей друг с другом. Соответствующие им системы уравнений решаются на Gs MIMD-процессах. В этом случае количество процессов зависит от числа подграфов, на которые разбивается СДОРП.

При общем для СДОРП шаге Δx разбиение графа приводит к неравномерности загрузки процессов. Выровнять загрузку можно такими путями:

1. Ставить в соответствие технологически определенным фрагментам графа большее, чем один, число процессов.
2. При формировании фрагментов набирать в них ветви с учётом технологического фактора и длины с таким расчётом, чтобы выравнивались суммарные длины ветвей по фрагменту.

Ввиду большого разнообразия длин первый путь является более предпочтительным. При его использовании можно взять данные по распределению загрузки на уровне 3.

Схема связи между виртуальными процессами и соотношение между количеством операций обмена и арифметических операций полностью зависит от разбиения графа.

Соединения между процессами осуществляются с использованиемтех же коммутирующих элементов 2×2, что и на уровнях 2 и 3.

Отображение «процесс – процессор» может быть легко организовано в современных многопроцессорных системах, так как количество процессов наиболее близко к реальным цифрам.

Выводы

Априорный анализ является важной задачей, непосредственно предшествующей выполнению девиртуализации разработанной модели РПМС.

Магистерская работа посвящена актуальной проблеме выполнения априорного анализа виртуальных параллельных моделей управляемого сетевого динамического объекта с распределенными параметрами.

В данной работе была обозначена актуальность разработок в данном направлении. Был выполнен анализ разработок по данному вопросу и рассмотрены основные предложенные подходы, концепции и общий математический аппарат априорного анализа.

Дальнейшая работа направлена на:

• Расширение математического описания сетевого объекта для приближения свойств модели к свойствам реальной сети.
• Расширение перечня критериев эффективности виртуальных параллельных моделей и их математическое описание.
• Получение на основе работы более конкретных рекомендаций для последующей девиртуализации модели.

При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2013 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Список источников

1. Anoprienko A.J., Svjatnyj V.A., Braunl T., Reuter A., Zeitz M.: Massiv parallele Simulationsumgebung fur dynamische Systeme mit konzentrierten und verteilten Parametern. // 9. Symposium ASIM’94, Tagungsband, Vieweg – 1994, S. 183-188.
2. Feldmann L.P., Svjatnyj V.A., Resch M., Zeitz M.: Forschungsgebiet: parallele Simulationstechnik. // Наукові праці Донецького національного технічного університету. Серія: Проблеми моделювання і автоматизації проектування [Электронный ресурс]. – Режим доступа: http://www.nbuv.gov.ua/portal/natural/Npdntu/Pm/2008/08flpfps.pdf.
3. Svjatnyj V.A.: Virtuelle parallele Simulationsmodelle und ein Devirtualisierungsvorgang der Entwicklung von parallelen Simulatoren fur dynamische Netzobjekte mit verteilten Parametern. Teil 4. // Vortrag am HLRS – 2008.
4. Молдованова О.В. Проблемно орієнтоване паралельне моделююче середовище для мережних динамічних об’єктів з розподіленими параметрами: Дис. канд. наук // 01.05.02 – 2008.
5. Святний В.А., Молдованова О.В., Чут А.М.: Стан та перспективи розробок паралельних моделюючих середовищ для складних динамічних систем з розподіленими та зосередженими параметрами // Наукові праці Донецького національного технічного університету. Серія: Інформатика, кібернетика та обчислювальні методи [Электронный ресурс]. – Режим доступа: http://www.nbuv.gov.ua/portal/natural/Npdntu/2008/ikot/08svasgt.pdf.
6. Войтов А.В., Святний В.А.: Апріорний аналіз віртуальної паралельної моделі другого рівня мережного динамічного об'єкта з розподіленими параметрами. // Наукові праці Донецького національного технічного університету. Серія: Динамічні системи, моделювання та чисельні методи [Электронный ресурс]. – Режим доступа: http://ea.donntu.ru:8080/jspui/bitstream/123456789/14354/1/6_Войтов.pdf.
7. Max-Planck-Institut fur Dynamik komplexer technischer Systeme. [Электронный ресурс]. – Режим доступа: http://www.mpi-magdeburg.mpg.de/.
8. Institut fur Parallele und Verteilte Systeme Universitat Stuttgart. [Электронный ресурс]. – Режим доступа: http://www.ipvs.uni-stuttgart.de/index1.html.
9. High Performance Computing Center Stuttgart. [Электронный ресурс]. – Режим доступа: http://www.hlrs.de/.
10. Science Experimental Grid Laboratory. [Электронный ресурс]. – Режим доступа: http://segl.hlrs.de/.
11. Schulz Roland: Parallele und Verteilte Simulation bei der Steuerung komplexer Produktionssysteme. Dissertation zur Erlangung des akademischen Grades eines Doktors der Wirtschaftswissenschaften. // Ilmenau – 2002.
12. Svjatnyj V.A.: Virtuelle parallele Simulationsmodelle und ein Devirtualisierungsvorgang der Entwicklung von parallelen Simulatoren fur dynamische Netzobjekte mit verteilten Parametern. Teil 6: Systemorganisation und Subsysteme verteilter paralleler Simulationsumgebung. Parallele blockorientierte Simulationssprache: ein Entwicklungskonzept. // Vortrag am HLRS – 2010.