ДонНТУ  Портал магістрів

Скорич Василь Ігорович

Факультет комп'ютерних наук та технологій

Кафедра комп'ютерної інженерії

Спеціальність "Комп'ютерні системи та мережі"

Апріорний аналіз віртуальних паралельних моделей керованого мережного динамічного об’єкта з розподіленими параметрами

Науковий керівник: д.т.н., проф. Святний Володимир Андрійович

Резюме Біографія Реферат

Реферат за темою випускної роботи

Зміст

• Вступ
• 1 Актуальність теми
• 2 Цілі і задачі досліджень
• 3 Концепція РПМС і принцип декомпозиції на підсистеми
• 4 Аналіз стану розробок
• 5 Математичний опис мережного динамічного об'єкта
• 6 Рівні розпаралелювання
• 6.1 Рівень 1: одне рівняння – один процес. Мінімальна гранулярність
• 6.2 Рівень 2: один елемент гілки (2 рівняння) – один процес
• 6.3 Рівень 3: одна гілка – один процес
• 6.4 Рівень 4: підграф мережевого об'єкта – один процес
• Висновки
• Список посилань

Вступ

У сучасному світі будь-яка високотехнологічна розробка потребує експериментального дослідження перед своїм впровадженням. Але проведення натурних експериментів зазвичай є важким або економічно невигідним. Рішенням даної проблеми є моделювання – вивчення необхідних властивостей об'єктів за допомогою розроблених математичних моделей реальних об'єктів.

З розвитком обчислювальної техніки найбільш актуальним напрямком стало комп'ютерне моделювання. Але постійно зростаюча складність об'єктів призводить до відповідного зростання витрат часу моделювання та потужності обчислювальних ресурсів. Однопоточні системи вже не справляються з сучасними навантаженнями задач моделювання. Отже, виникає необхідність розробки і впровадження багатопотокових моделюючих систем.

Впровадження нових концепцій моделювання призвело до появи нових проблем, а саме – необхідності створення формалізованого підходу до розробки і побудови складних проблемно-орієнтованих паралельних систем. Так з'явилася концепція розподіленого паралельного моделюючого середовища (РПМС).

1. Актуальність теми

Об’єктом, що обробляється на РПМС, є мережний динамічний об’єкт з розподіленими або зосередженими параметрами (МДОРП та МДОЗП) – формальний опис, що містить формалізоване топологічне подання та системи рівнянь фізичних процесів складної динамічної системи (СДС), що об’єднує їх за допомогою векторно-матричних виразів та операцій.

Дослідження та розробка такої системи є актуальним та перспективним напрямком. А завдяки принципу декомпозиції розробка кожної підсистеми РПМС є відносно незалежною задачею з рядом конкретних проблем.

Із ускладненням цільових систем для паралельного моделювання постає проблема обрання оптимальної її побудови та складу. Проведення подібної оцінки на етапі розробки, девіртуалізації та імплементації системи дозволяє значно скоротити економічні, часові та ресурсні витрати та отримати при цьому найбільш продуктивну систему. Також важливим є передбачення показників прискорення при розпаралелюванні та подальшому нарощуванні системи, що дозволяє зробити висновок про її економічну ефективність. Саме такі задачі вирішує система апріорного аналізу.

2. Цілі і задачі досліджень

Метою роботи є дослідження методів та підходів до вирішення задачі апріорного аналізу віртуальних паралельних моделей керованого мережного динамічного об'єкта з розподіленими параметрами.

Для досягнення поставлених цілей необхідно вирішити ряд завдань:

• Розробка математичного опису мережного об'єкта.
• Визначення переліку критеріїв ефективності віртуальних паралельних моделей.
• Математичний опис критеріїв ефективності.
• Розробка системи програмної підтримки апріорно аналізу.
• Розробка рекомендацій для девіртуалізації моделі.
• Проведення тестів і модельних експериментів.

3. Концепція РПМС і принцип декомпозиції на підсистеми

Концепція РПМС для СДС з розподіленими і зосередженими параметрами запропонована в 1992 році в рамках співпраці Донецького національного технічного університету та Інституту паралельних і розподілених систем (IPVS) Штутгартського університету (Німеччина). Вона була опублікована в доповіді [1] і розвинена в роботі [2].

Згідно з [2] РПМС – це дружня до користувача системна організація апаратного забезпечення, системного і цільового моделюючого програмного забезпечення, яка підтримує всі етапи розробки та реалізації МДОРП і МДОЗП. Ключовим завданням є розробка повнофункціонального РПМС, що задовольняє наступним параметрам:

• Використання вже існуючих SIMD і MIMD-архітектур в РПМС.
• Розробка повнофункціонального програмного забезпечення для моделювання SIMD і MIMD-компонентів РПМС згідно з вимогами динамічної системи.
• Моделювання динамічних систем з зосередженими та розподіленими параметрами на загальній методичній основі.
• Розробка спеціалізованого програмного забезпечення для опису паралельних процесів.
• Об'єктно-орієнтована реалізація моделюючого програмного забезпечення.
• Наявність засобів для роботи на всіх етапах розробки СДС.
• Високоінтелектуальна діалогова підтримка користувача на всіх етапах розробки і моделювання СДС.

Розробка такої повнофункціональної системи є надзвичайно складним завданням. Для вирішення цієї проблеми в роботі [2] вказується на доцільність декомпозиції складної системи РПМС на декілька підсистем. При цьому розробка кожної з таких підсистем може проводитися відносно незалежно від інших.

Згідно запропонованої концепції РПМС повинна складатися з таких підсистем:

• підсистема діалогу;
• підсистема топологічного аналізу;
• підсистема генерації рівнянь;
• підсистема віртуальних паралельних моделей;
• підсистема паралельних вирішувачів рівнянь;
• підсистема обміну даними;
• підсистема балансування навантаження;
• підсистема візуалізації;
• підсистема баз даних;
• підсистема IT-підтримки.

Апріорний аналіз безпосередньо взаємодіє з підсистемами віртуальних паралельних моделей, підсистемою балансування навантаження і обміну даними і тісно пов'язаний з процесом девіртуалізації віртуальної паралельної моделі.

Девіртуалізація моделі складної динамічної системи – це її перетворення за методами і алгоритмам, що забезпечують оптимальне виконання заявки на моделювання СДС в цільовій паралельній обчислювальній системі.

Апріорна оцінка паралельної віртуальної моделі на етапі девіртуалізації дозволяє визначити оптимальні підходи до її розпаралелювання шляхом розгляду можливих рівнів розпаралелювання та варіантів, які мають якісно кращі показники за рівномірністю завантаження процесів та за обсягом передачі даних.

4. Аналіз стану розробок

Задача апріорного аналізу з’явилась разом з появою паралельних обчислювальних систем. Вирішенню даної проблеми присвячено певне число робіт, але закінченого програмно-апаратного рішення не існує.

Основною роботою у напрямку апріорного аналізу віртуальних моделей є [3]. В ній докладно розглядаються основні теоретичні питання на базі конкретних прикладів в реальних галузях промисловості. В роботі чітко окреслена концепція системи та математичний базис.

Так, згідно з [3], головними цілями апріорного аналізу є:

• розгляд можливих підходів до розпаралелювання та структурного представлення МДОРП, розпочинаючи з мінімально гранулярних процесів;
• дослідження та порівняння рівнів розпаралелювання за критеріями розподілення навантаження, обміну даними та синхронізації процесів;
• пропонування та перевірка можливих альтернативних рішень щодо організації рівнів розпаралелювання;
• проведення загального порівняння рівнів розпаралелювання та формулювання рекомендацій щодо подальшої імплементації моделі на цільову обчислювальну систему.

Основними показниками апріорного аналізу є [3]:

• рівномірність завантаження віртуальних процесів. Під завантаженням у даному випадку розуміють кількість операцій, що виконується процесом;
• співвідношення між арифметичними операціями та операціями обміну даними;
• приріст прискорення обчислень за умов збільшення кількості процесів;
• упорядкування процесів на реальні процесори при імплементації моделі на цільову обчислювальну систему.

В літературі [3, 4] також зазначається, що апріорний аналіз виконується для віртуальних паралельних моделей чотирьох рівнів розпаралелювання, що наведені на рис. 1.

Перший рівень – рівень процесів мінімальної гранулярності. Визначається співвідношенням "одне рівняння – один процес".

На другому рівні розпаралелювання кожному процесу ставиться у відповідність елемент гілки графа. Для цього рівня характерним є співвідношення "один елемент – один процес".

Третій рівень – рівень розпаралелювання типу "один вузол – один процес" та "одна гілка – один проце".

Четвертий рівень – це декомпозиція графа на підргафи, що мають найменшу кількість зв’язків один з одним. У цьому випадку кількість процесів залежить від числа підграфів, на які розбивають МДОРП.

Слід зазначити, що роботи з апріорного аналізу паралельних моделей велись в ДонНТУ в контексті розробки окремих підсистем РПМС, але їм не приділялась спеціальна увага.

Так у роботі [5] зазначається, що апріорний аналіз віртуальної паралельної моделі є невід’ємним та важливим під час процесу девіртуализації віртуальної паралельної моделі та її імплементації.

Можна виділити роботу [6], де окремо виконаний апріорний аналіз мережного динамічного об’єкта з розподіленими параметрами на другому рівні розпаралелювання.

Слід зазначити, що проблемами паралельного моделювання активно займаються європейські інститути ([7], [8], [9]).

Так, в High Performance Computing Center Stuttgart активно розробляється система SEGL – сучасний інструмент для опису і виконання багатовимірних програм на розподілених високопродуктивних обчислювальних ресурсах. [10]

Також в якості прикладу можна виділити роботу [11], метою якої є розробка основ застосування розподілених і паралельних систем моделювання. Основна увага приділяється моделюванню складних виробничих процесів, приводиться обґрунтування ефективності таких систем у сучасних технологічних процесах. Мета даної роботи полягає у визначенні основних принципів досягнення прискореного виконання моделювання за рахунок розподілу та розпаралелювання.

5. Математичний опис мережного динамічного об'єкта

Під мережним динамічним об'єктом розуміють сукупність елементів, пов'язаних між собою фізичними вузлами, через які здійснюються цілеспрямовані розподіли потоків (електричного струму, потоків рідин і газів і т.п.) [4].

Мережний динамічний об'єкт характеризується топологією – розташуванням гілок і вузлів їх перетину, активних і пасивних елементів і т.д. Топологія може бути представлена у вигляді технологічних схем, графів, структур автоматизованих систем або їх поєднанням.

Фізичні процеси, що відбуваються в моделі, описуються за допомогою системи диференційних рівнянь в частинних похідних (приклад наведено для керованого мережного динамічного об'єкта – вентиляційної шахти):

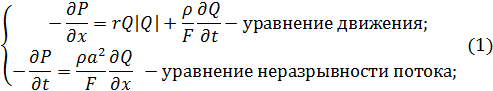
де P(x, t) – тиск;

Q(x, t) – витрата повітря;

r – питомий аеродинамічний опір повітропроводу;

ρ – густина повітря;

F – площа перерізу повітропроводу;

а – швидкість звуку в повітрі;

х – просторова координата вдовж осі повітропроводу в межах його довжини.

Граничними умовами для (1) є функції тиску в початковому та кінцевому вузлах гілки. За типом граничних умов гілки поділяються на три типи [12]:

• гілки, що інциденті внутрішнім вузлам мережі, в яких тиск розраховується в процесі вирішення мережної системи рівнянь відповідно до вузлових динамічних умов;

  

  де P_wi – тиск в вузлі wi;

  Q_wi – загальні витрата повітря через вузол wi;

  F_wi – площа поперечного перерізу вузла;

• гілки, що інцидентні вузлу підключення вентилятора; в цьому вузлі тиск задається як характеристика вентилятора

P_wj=P_FANj (3)

• гілки, що інциденті вузлу виходу в атмосферу; тут задається постійний тиск

P_wj=P_ATM=const (4)

Для моделювання мережного динамічного об'єкта (МДО) необхідно провести його формальний опис (модель), яке включає:

• таблицю кодування і топологічні характеристики, які можуть бути отримані з неї і використані в рівняннях;
• m пар рівнянь типу (1), записаних для кожної гілки МДО

• n₁ вузлових граничних умов – тисків в вузлах;
• n₂ характеристик вентиляторів (або інших активних елементів);
• n₃ відкритих виходів в атмосферу, де тиски приймаються постійними та рівними атмосферному тиску.

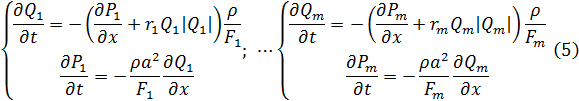
Таким чином, мережний об'єкт з розподіленими параметрами описується m системами рівнянь (1) з n = n1 + n2 + n3 граничними умовами, де m – число гілок графа, n₁, n₂, n₃ – кількість вузлів з умовами (2), (3), (4) відповідно.

Усі гілки графа апроксимуються за просторовими координатами згідно зі схемою, наведеною на рис. 2.

M = l_i/Δx – кількість елементів, на які розбивається гілка;

l_i – довжина гілки;

Δx – крок.

Для k-ого елемента гілки Q_j рівняння (5) записуються у вигляді, зручному для застосування чисельних методів (просторово дискретизована Simulation Model, ПДSM):

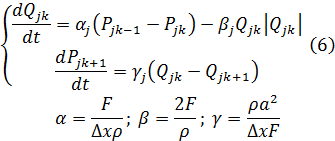
В (6) просторова координата x розглядається як дискретна, а час t залишається неперервним. Похідна за дискретною змінною замінена різницею.

При цьому для всієї мережі j ∈ (1, 2, … m), індекс k = 1, 2, … M_j в межах кожної гілки, а M_j залежить від довжини гілки і кроку Δx апроксимації по просторовій координаті.

Граничні умови для рівнянь повітряних потоків в гілках діляться на зовнішні і внутрішні. До зовнішніх відносяться тиски в початкових вузлах, чиї гілки з'єднані з атмосферою, і тиски у вузлах, до яких підключені вентилятори. Внутрішні граничні умови – це тиски у вузлах мережі, які повинні бути обчислені при вирішенні системи рівнянь.

Внутрішні граничні умови визначаються у відповідності з наступним рівнянням:

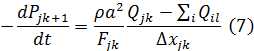
де ∑_iQ_il – алгебраїчна сума витрат в елементах гілок, інцидентних граничному вузлу,

i – номер гілки,

l = 1 (якщо гілка виходить з вузлу), M_i (якщо гілка входить в вузол)

M_i – число елементів, що апроксимують i-у гілку.

У загальному випадку граничні умови є змінними типу P, які обчислюються за рівняннями нерозривності в граничних точках апроксимації гілок M_j+1, що співпадають з вузлами мережі:

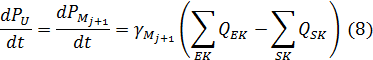
де Q_SK і Q_EK – витрати повітря на початку і кінці гілки відповідно.

На основі рівнянь (6) і (7) повинна генеруватися система рівнянь, що апроксимує систему (5), для всієї мережі.

6. Рівні розпаралелювання

6.1 Рівень 1: одне рівняння – один процес. Мінімальна гранулярність

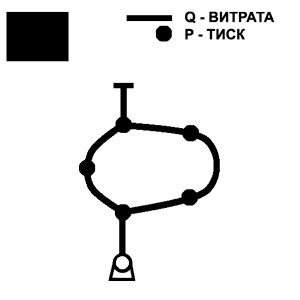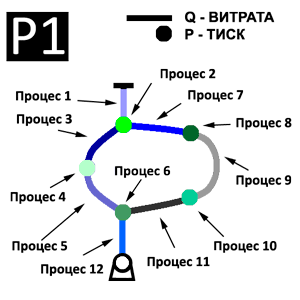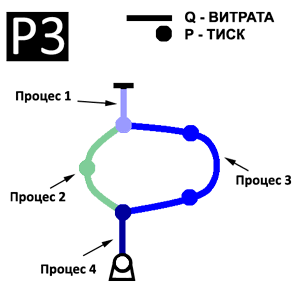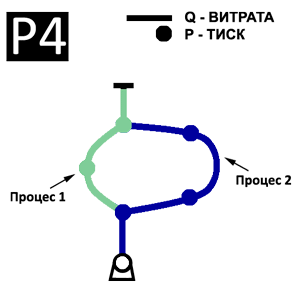
Структура віртуальної паралельної Simulation Model (ВПSM) однієї гілки мережного об'єкта, дискретизованого за просторовою координатою M елементами, представлена на рис. 3.

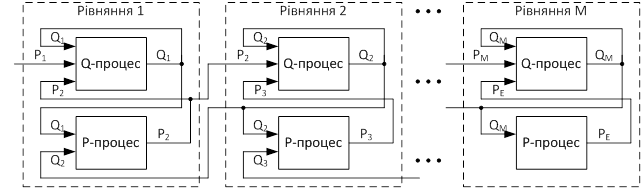
Тут Q- та P-процеси забезпечують рішення рівняння (6).

Завантаження віртуальних процесів

Завантаження визначається складом операцій, необхідних для вирішення Q- і P-рівнянь.

З (6) видно, що права частина Q-рівняння відрізняється від правої частини P-рівняння наявністю доданка β_jQ_jk|Q_jk|. Тривалість виконання операцій становить

T_Q=t_mul+t_sum+t_mod=2t_sum+3t_mul+t_mod (9)

T_P=t_mul+t_sum (10)

де t_mul, t_sum, t_mod – відповідно тривалості операцій множення, алгебраїчного додавання і визначення модуля змінної.

Час нерівномірності

ΔT=T_Q–T_P=t_mod+2t_mul (11)

не залежить від обраного чисельного методу і вказує на те, що Р-процеси не довантажені майже в 2 рази.

Таким чином, рівню процесів мінімальної гранулярності притаманна нерівномірність завантаження, яка призводить до втрати ефективності паралельного виконання процесів.

Співвідношення між обсягами обчислювальних та допоміжних операцій

Як видно на рис. 3, кожен Q-процес має три вхідні змінні і одну вихідну, а Р-процес – дві вхідні і одну вихідну змінні. З огляду на те, що змінна Q_k, що обчислюється в k-му елементі, є змінною зворотного зв'язку (рис. 3), то відсутня необхідність організовувати передачу Q_k з виходу на вхід в Q-процесі. Таким чином, Q-процес повинен виконати такі допоміжні операції:

• введення P_k з k-ого Р-процесу;
• введення P_k+1 з k+1-ого Р-процесу;
• посилка Q_k k-ому Р-процесу;
• посилка Q_k k+1-ому Р-процесу.

У свою чергу, Р-процес повинен виконувати наступні операції:

• посилка P_k k–1-му Q-процесу;
• посилка P_k k-му Q-процесу;
• введення Q_k-1 з k–1-ого Q-процесу;
• введення Q_k з k-ого Q-процесу.

Таким чином, на кожному кроці обчислень Q- і Р-процеси повинні виконати по 4 операції обміну даними. По відношенню до Q-процесу, де згідно з 9) виконується 6 обчислювальних операцій, операції обміну становлять відповідно 2/3. По відношенню до Р-процесів, де число обчислювальних операцій відповідає формулі (10), операції обміну становлять 4/2 = 2.

Загалом на 8 операцій рівнянь виду (6) повинно виконуватися по 8 операцій обміну.

Схема зв'язку між віртуальними процесами

На рис. 3 показана взаємодія Q- і Р-процесів за їх входами і виходами. Пропонуються віртуальні PQ- і QP-комутатори, що складаються з елементів перемикачів (рис. 4).

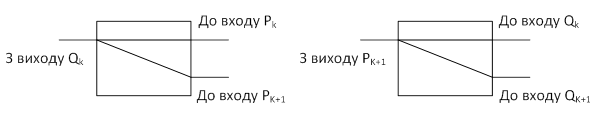
Змінна Q_k (вихід Q-процесу) дублюється і підключається на вхід процесів P_k, P_k+1. Змінна P_k+1 (вихід P-процесу) після подвоєння підключається на вхід процесів Q_k, Q_k+1.

Для мінімізації часу обміну T_exch робота віртуального комутатора повинна бути організована таким чином:

1. Схема з'єднань реалізується до початку вирішення і залишається незмінною на весь період моделювання.
2. В i-му циклі рішення запам'ятовуються значення компонент векторів по мірі їх обчислення і записуються в регістри виходів Q- і Р-процесів.
3. По завершенні циклу "обчислення – запис" найдовшим процесом всі процеси синхронізуються.
4. Синхронно для всіх Q- і Р-процесів активуються команди посилки і отримання, в один такт на входах Q- і Р-процесів з'являються актуальні значення змінних і на наступному такті записуються в пам'ять.
5. Запускається i+1-ий цикл рішення.

За такої організації роботи комутатора і паралельної передачі всіх розрядів Q- і Р-чисел час обміну буде визначатися формулою

T_exch=t_regwr+t_regrd+t_trans+t_rec+t_wr (12)

де t_regwr – час запису в регістр у найдовшому Q-процесі;

t_regrd – час зчитування з регістра;

t_trans – час передачі по лінії зв'язку;

t_rec – час прийому з лінії зв'язку в регістр;

t_wr – час запису з регістра в пам'ять.

Співвідношення "процес - процесор" при відображенні на віртуальну і цільову паралельні архітектури

На першому рівні необхідна наступна кількість процесорних елементів N_PE1 для обчислення витрат повітря і тисків гілок:

N_PE1=2∑^m_j=1M_j (13)

Тут m – кількість гілок в мережевому об'єкті, M_j – кількість елементів в гілках. У свою чергу M_j визначається довжиною гілки і кроком апроксимації за просторовою координатою Δx:

M_j=l_j/Δx (14)

Через те, що величина Δx для всієї мережі повинна бути однаковою, число процесів визначається сумарною довжиною гілок:

N_PE1=(2/Δx)∑^m_j=1l_j (15)

Звідси випливає, що перший рівень розпаралелювання вимагає таку кількість віртуальних процесів і процесорів, яка істотно перевищує технічні можливості доступних користувачам MIMD-систем.

За формулою (15) можна зробити оцінку можливого кроку Δх і параметрів M_j, які може забезпечити цільова паралельна MIMD-система з відомим числом процесорів N_TCA:

Δx_POSS=(2/N_TCA)∑^m_j=1l_j (16)

6.2 Рівень 2: один елемент гілки (2 рівняння) – один процес

Рівномірність завантаження процесів

Співвідношення один елемент гілки – один процес означає, що система рівнянь (6) для k-ого елемента (1 ≤ k ≤ M_j) гілки j (1 ≤ j ≤ m) вирішується у відповідному k-му MIMD-процесі. Віртуальна паралельна модель для однієї гілки показана нарис. 5.

Завантаження процесів обчисленнями збільшилась, час обчислення правих частин у k-му процесі становить

T_QP=T_Q+T_P (17)

Для простих гілок T_Q, T_P обчислюються за формулами (9), (10), і T_QP складе:

T_QPmin=2t_sum+t_mod+3t_mul+t_sum=3t_sum+4t_mul+t_mod (18)

Співвідношення між обсягами обчислювальних та допоміжних операцій

Для рівня 2 співвідношення змінюється в бік зменшення частки операцій обміну. З рис. 5 випливає, що k-й процес j-ої гілки (QP)_jk виконує такі допоміжні операції:

• введення P_k з сусіднього k–1-ого процесу;
• введення Q_k+1 з сусіднього k+1-ого процесу;
• посилка Q_k сусідньому k–1-ому процесу;
• посилка P_k+1 сусідньому k+1-ому процесу.

Так, на 8 операцій при обчисленні правої частини рівнянь виду (6) повинно виконуватися 4 операції обміну.

Таким чином, на рівні "один елемент гілки – один процес" вдвічі поліпшується співвідношення між обсягом обчислень і операцій обміну.

Схема зв'язку між віртуальними процесами

Схема зв'язку випливає з структури ВПSM (рис. 5). Процес (QP)_jk для k-ої гілки має схему зв'язків з сусідніми процесами (QP)_jk-1, (QP)_jk+1, показану на рис. 6.

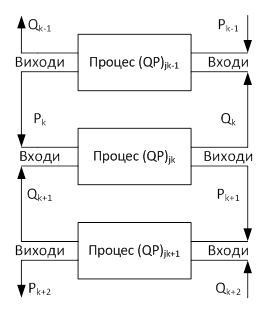
Зв'язок між сусідніми процесами здійснюється комутуючими елементами 2×2 з перехресним включенням. На даному рівні розпаралелювання легко об'єднуються вузлові процеси P_U з будь-яким з Q-процесів інцидентної гілки.

Співвідношення "процес – процесор" при відображенні на віртуальну і цільову паралельні архітектури

Віртуальна паралельна модель рівня 2 вимагає для МДОРП наступну кількість віртуальних процесів:

N_PE2=∑^m_j=1M_j (19)

З урахуванням (14) маємо:

N_PE2=(1/Δx)∑^m_j=1l_j (20)

Ця кількість процесів в значно більшій мірі відповідає кількості процесорів в сучасних MIMD-системах.

При відомій кількості процесорів N_TCA маємо можливий крок

Δx_POSS=(1/N_TCA)∑^m_j=1l_j (21)

6.3 Рівень 3: одна гілка – один процес

Рівномірність завантаження процесів

Рівень розпаралелювання "1 гілка – 1 процес" повинен мати m QP-процесів, що вирішують системи рівнянь відносно змінних Q_jk, P_jk+1 j-ої гілки (k = 1, 2, …, M_j), а також n P_U-процесів, що вирішують вузлові рівняння і дають граничні тиски у вузлах для всіх гілок. Розрахунки P_U можуть бути суміщені з QP-процесами передвузлових елементів гілок і, отже, немає необхідності виділяти окремо P_U-процеси.

Завантаження процесів визначається кількістю розв'язуваних рівнянь і становить по гілках

L_j=2M_j=2l_j/Δx (22)

З огляду на те, що гілки мають різні довжини, завантаження буде змінюватися в межах

L_min≤L_j≤L_max (23)

де L_min, L_max – відповідно завантаження по гілках мінімальної і максимальної довжини.

Нерівномірність довжин становить

ΔL=L_max–L_min=2(M_jmax–M_jmin) (24)

Знаючи час виконання QP-процесу рівня 2, можна оцінити максимальний час очікування по всьому об'єкту

T_Wmax=ΔL·T_QP (25)

і часи очікування по процесах всіх гілок по відношенню до процесу гілки l_max:

T_Wj=ΔL_j·T_QP (26)

де ΔL_j=L_max–L_j.

Довжини виробок шахтних вентиляційних мереж мають розкид у кілька разів. Тому нерівномірність завантаження процесів буде дуже істотною. Пропонується модифікація даного рівня розпаралелювання: "1 процес – 1 гілка мінімальної довжини l_jmin". При цьому кількість підгілок в кожній гілці складе N_Pj=l_j/l_min.

Співвідношення між обсягами обчислювальних та допоміжних операцій

Співвідношення покращилось в бік зменшення частки допоміжних операцій. Процес-гілка вирішує 2M_j рівнянь і виконує такі допоміжні операції:

• введення P_j1 із вузлового процесу, інцидентного початковому вузлу;
• введення витрат початкових елементів гілок, інцидентних кінцевому вузлу j-ої гілки;
• посилка витрати Q_j1 процесу початкового вузла;
• посилка обчисленого тиску P_jM_j+1 в кінцевому вузлі гілки Q_j, процесам, що обчислюють витрати Q_j1 в інцидентних гілках.

Таким чином, на 8М_j обчислювальних операцій рівнянь виду (6) повинно виконуватися, аналогічно другому рівню, 4 операції обміну.

На рівні 3 у варіанті "1 гілка – 1 процес" у М_j раз поліпшується співвідношення між обсягом обчислень і кількістю операцій обміну по кожній гілці.

У варіанті "1 гілка – 1 процес" кожній гілці відповідає N_Pj+1 процес. Зі структури процесів випливає, що кожен з них вирішує не менше M_min=l_jmin/Δx пар рівнянь виду (6) і при цьому виконує такі допоміжні операції:

• введення P_jk з останнього елемента сусіднього процесу;
• введення Q_jk+h з першого елемента сусіднього процесу (h ≤ M_min – крок за кількістю елементів у процесах);
• введення Q_jk з першого елемента на останній елемент сусіднього процесу;
• введення P_jk+h з останнього елемента на перший елемент сусіднього процесу.

Звідси випливає, що число допоміжних міжпроцесорних операцій обміну залишилося рівним 4. Таким чином, на 8Мmin операцій по обчисленню правих частин рівнянь виду (6) повинно виконуватися 4 операції обміну.

По відношенню до варіанту 1 частка обмінів вище, адже на кожну гілку ми ввели більше число процесів у M_j/М_min разів. При цьому покращилась рівномірність завантаження процесів.

Схема зв'язку між віртуальними процесами

Зі структури процесів випливає, що схеми зв'язку між j процесами і процесами підгілок, інцидентних вузлам, аналогічні. Процеси містять M_min QP-процесів другого рівня, які обчислюють змінні j-ої гілки від k = 1 до M_min (перший процес), k = M_min + 1 до k = 2M_min (другий процес) і т.д. За схемою зв'язку останній підпроцес QP_jM_min посилає першому підпроцесу QP_jM_min+1 сусіднього процесу тиск P_jM_min+1 і приймає від нього витрату Q_jM_min+1. Так само останній підпроцес QP_j2M_min сусіднього процесу посилає тиск P_j2M_min+1 своєму сусіду і приймає від нього витрату Q_j2M_min+1. Якщо число елементів у процесах менше M_min, то схема зв'язку залишається без змін і точно відповідає схемі на рис. 6: передача тисків і витрат здійснюється через комутуючі елементи 2×2. Їх число на кожну гілку на одиницю менше числа процесів, тобто N_Pj – 1.

Таким чином, віртуальний комутатор для ВПSM на третьому рівні розпаралелювання будується аналогічно комутатору другого рівня на базі комутуючих елементів 2×2.

Співвідношення "процес – процесор" при відображенні на віртуальну і цільову паралельні архітектури

Варіанти 1 і 2 віртуальної паралельної моделі рівня 3 вимагають для МДОРП наступної кількості процесів:

N⁽¹⁾_PE3=m (27)

N⁽²⁾_PE3=N_P=∑^m_j=1N_Pj+(m–m_ml) (28)

З урахуванням того, що N_Pj=l_j/l_min, отримаємо

N⁽²⁾_PE3=(1/l_min)∑^m_j=1l_j+(m–m_ml) (29)

Тут m_ml – кількість гілок з довжиною lmin;

(m – m_ml) – кількість додаткових процесів в гілках з l_j > l_min.

При відображенні на віртуальні паралельні системи співвідношення "1 процес – 1 процесор" є природним. Відображення на цільову паралельну обчислювальну систему з співвідношенням "1 процес – 1 процесор" можливо як по N_PE3⁽¹⁾, так і по N_PE3⁽²⁾.

6.4 Рівень 4: підграф мережевого об'єкта – один процес

При такому підході до розпаралелювання граф мережевого об'єкта розбивається на Gs підграфів, що мають найменшу кількість зв'язків один з одним. Відповідні їм системи рівнянь вирішуються на Gs MIMD-процесах. У цьому випадку кількість процесів залежить від числа підграфів, на які розбивається МДОРП.

При загальному для МДОРП кроці Δx розбиття графа призводить до нерівномірності завантаження процесів. Вирівняти завантаження можна такими шляхами:

1. Ставити у відповідність технологічно визначеним фрагментам графа більше, ніж один, число процесів.
2. При формуванні фрагментів набирати в них гілки з урахуванням технологічного фактора і довжини з таким розрахунком, щоб вирівнювались сумарні довжини гілок у фрагменті.

Зважаючи на велику різноманітність довжин перший шлях є кращим. При його використанні можна взяти дані з розподілу завантаження на рівні 3.

Схема зв'язку між віртуальними процесами і співвідношення між кількістю операцій обміну і арифметичними операціями повністю залежить від розбиття графа.

З'єднання між процесами здійснюються з використанням тих самих комутуючих елементів 2×2, що і на рівнях 2 і 3.

Відображення "процес – процесор" може бути легко організовано в сучасних багатопроцесорних системах, адже кількість процесів найбільш близька до реальних цифр.

Висновки

Апріорний аналіз є важливим завданням, що безпосередньо передує виконанню девіртуалізації розробленої моделі РПМС.

Магістерська робота присвячена актуальній проблемі виконання апріорного аналізу віртуальних паралельних моделей керованого мережного динамічного об'єкта з розподіленими параметрами.

У даній роботі була позначена актуальність розробок у даному напрямку. Був виконаний аналіз розробок з даного питання і розглянуті основні запропоновані підходи, концепції та загальний математичний апарат апріорного аналізу.

Подальша робота спрямована на:

• Розширення математичного опису мережного об'єкта для наближення властивостей моделі до властивостей реальної мережі.
• Розширення переліку критеріїв ефективності віртуальних паралельних моделей та їх математичний опис.
• Отримання на основі роботи більш конкретних рекомендацій для подальшої девіртуалізації моделі.

При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2013 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після вказаної дати.

Список посилань

1. Anoprienko A.J., Svjatnyj V.A., Braunl T., Reuter A., Zeitz M.: Massiv parallele Simulationsumgebung fur dynamische Systeme mit konzentrierten und verteilten Parametern. // 9. Symposium ASIM’94, Tagungsband, Vieweg – 1994, S. 183-188.
2. Feldmann L.P., Svjatnyj V.A., Resch M., Zeitz M.: Forschungsgebiet: parallele Simulationstechnik. // Наукові праці Донецького національного технічного університету. Серія: Проблеми моделювання і автоматизації проектування [Електронний ресурс]. – Режим доступу: http://www.nbuv.gov.ua/portal/natural/Npdntu/Pm/2008/08flpfps.pdf.
3. Svjatnyj V.A.: Virtuelle parallele Simulationsmodelle und ein Devirtualisierungsvorgang der Entwicklung von parallelen Simulatoren fur dynamische Netzobjekte mit verteilten Parametern. Teil 4. // Vortrag am HLRS – 2008.
4. Молдованова О.В. Проблемно орієнтоване паралельне моделююче середовище для мережних динамічних об’єктів з розподіленими параметрами: Дис. канд. наук // 01.05.02 – 2008.
5. Святний В.А., Молдованова О.В., Чут А.М.: Стан та перспективи розробок паралельних моделюючих середовищ для складних динамічних систем з розподіленими та зосередженими параметрами // Наукові праці Донецького національного технічного університету. Серія: Інформатика, кібернетика та обчислювальні методи [Електронний ресурс]. – Режим доступу: http://www.nbuv.gov.ua/portal/natural/Npdntu/2008/ikot/08svasgt.pdf.
6. Войтов А.В., Святний В.А.: Апріорний аналіз віртуальної паралельної моделі другого рівня мережного динамічного об'єкта з розподіленими параметрами. // Наукові праці Донецького національного технічного університету. Серія: Динамічні системи, моделювання та чисельні методи [Електронний ресурс]. – Режим доступу: http://ea.donntu.ru:8080/jspui/bitstream/123456789/14354/1/6_Войтов.pdf.
7. Max-Planck-Institut fur Dynamik komplexer technischer Systeme. [Електронний ресурс]. – Режим доступу: http://www.mpi-magdeburg.mpg.de/.
8. Institut fur Parallele und Verteilte Systeme Universitat Stuttgart. [Електронний ресурс]. – Режим доступу: http://www.ipvs.uni-stuttgart.de/index1.html.
9. High Performance Computing Center Stuttgart. [Електронний ресурс]. – Режим доступу: http://www.hlrs.de/.
10. Science Experimental Grid Laboratory. [Електронний ресурс]. – Режим доступу: http://segl.hlrs.de/.
11. Schulz Roland: Parallele und Verteilte Simulation bei der Steuerung komplexer Produktionssysteme. Dissertation zur Erlangung des akademischen Grades eines Doktors der Wirtschaftswissenschaften. // Ilmenau – 2002.
12. Svjatnyj V.A.: Virtuelle parallele Simulationsmodelle und ein Devirtualisierungsvorgang der Entwicklung von parallelen Simulatoren fur dynamische Netzobjekte mit verteilten Parametern. Teil 6: Systemorganisation und Subsysteme verteilter paralleler Simulationsumgebung. Parallele blockorientierte Simulationssprache: ein Entwicklungskonzept. // Vortrag am HLRS – 2010.