Шевченко Алексей Олегович
Факультет компьютерных наук и технологий
Кафедра программного обеспечения интеллектуальных систем
Специальность Программное обеспечение систем
Исследование способов оптимизации игрового искусственного интеллекта за счет повышения эффективности поиска пути агентами
Научный руководитель: к.т.н. доц. Жук Александр Викторович
Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Методы нахождения кратчайших путей
- 2.1 Алгоритм Дейкстры
- 2.2 Алгоритм А*
- 2.3 Алгоритм Jump Point Search (JPS)
- 3. Методы локальных уклонений
- 3.1 Скоростное препятствие
- 3.2 Взаимное скоростное препятствие
- 4. Методы построения пути на навигационной поверхности
- 4.1 Перемещение по полигонам
- 4.2 Перемещения используя грани полигонов
- 4.3 Перемещение по точкам
- 4.4 Гибридный метод
- 4.5 Сглаживание пути
- 5. Решение проблем использования методов скоростных ограничений на навигационной поверхности
- 5.1 Обеспечение навигации вдоль проложенного маршрута и одновременный анализ возможных коллизий
- 5.2 Учёт ограничений на проходимость карты при расчёте локального уклонения
- 5.3 Повторное прокладывание маршрута после выполнения локального уклонения
- Выводы
- Список источников
Введение
Теория нахождения кратчайших путей имеет большое значение в современном мире. Благодаря своему широкому применению, она в последнее время интенсивно развивается: наряду с совершенствованием уже существующих методов разрабатываются принципиально новые.
Множество задач оптимизации связаны именно с поиском кратчайших путей. Как результат — поиск пути в современном мире используется практически везде: от систем глобального позиционирования для нахождения кратчайшего маршрута среди городских улиц и путей между городами, в военных и гражданских системах автопилотирования, в транспортно-экспедиторском обслуживании – и вплоть до компьютерных игр.
Алгоритмы поиска кратчайших путей делятся на два типа.
- Поиск пути на дискретном рабочем поле (ДРП).
- Поиск пути на графе.
Оба класса алгоритмов имеют свои достоинства и недостатки, а так же свою область применения. Первый класс алгоритмов явлется достаточно простым, но дает не всегда хорошие резуьтаты, поэтому в данной работе будет рассматриваться второй класс.
Но нахождение кратчайшего пути это не единственная проблема. После нахождения кратчайшего пути в точку назначения некоторому агенту необходимо пройти этот путь так, чтобы не помешать другим агентам перемещающимся рядом. Для решения этой проблемы так же существует ряд алгоритмов которые обеспечивают всем агентам безопасный путь к точке назначения с минимальными отклонениями от проложенного пути и за минимальное время.
1. Актуальность темы
Современные видеоигры – это очень сложные программы, к которым предъявляются очень серьезные требования. Все происходящее на экране должно быть максимально реалистично, а так же максимально быстро. Если не будет хоты бы одного из этих требований, пользователям будет просто скучно.
Сегодня существует достаточно много различных алгоритмов и методик поиска кратчайшего пути и обхода движущихся препятствий на некоторой виртуальной карте. Но все эти методы работают сами по себе, но не рассчитаны на работу сообща, либо не учитывают каких то незначительных особенностей. Так, например, методы обхода движущихся препятствий не учитывают статические препятствия, а методы поиска пути не учитывают размеров агента при прокладывании пути.
Учитывая все вышеперечисленное, актуальной задачей является комбинирование методов поиска пути и локальных уклонений на карте представленной навигационной поверхностью для создания максимально реалистичного поведения, логичного и быстрого перемещения агентов на карте.
2. Методы нахождения кратчайших путей
В областях теории графов имеется несколько алгоритмов, которые могут искать пути на поверхности со сложными препятствиями и взвешенными областами. В литературе, многие из этих алгоритмов представлены в терминах изменения состояний или прохода по узлам графа. Это зачастую используется для решения множества проблем, включая пятнашки
и кубик Рубика, где состоянием является сочетание цифр или кубиков, и соседние состояния (или смежные узлы) посещаются путем перемещения цифр или поворота граней кубика. Применение этих алгоритмов к поиску пути в геометрическом пространстве требует простой адаптации: состояние или узел графа представляют объект, находящийся в определенной клетке, и передвижение в соседние клетки соответствует перемещению в соседние состояния или смежные узлы.
Далее следует описание алгоритмов поиска пути, от простых к более сложным.
2.1 Алгоритм Дейкстры
Е. Дейкстра разработал классический алгоритм для прохода по графам [1], грани которых имеют различный вес. На каждом шаге, он ищет необработанные узлы близкие к стартовому, затем просматривает соседей найденного узла, и устанавливает или обновляет их соответствующие расстояния от старта. Этот алгоритм принимает во внимание стоимость или длину пути и обновляет узлы, если к ним найден лучший путь. На рисунке 1 показана хорошая адаптация алгоритма к стоимости местности. Однако, он имеет слабость поиска в ширину, игнорируя направление к цели.
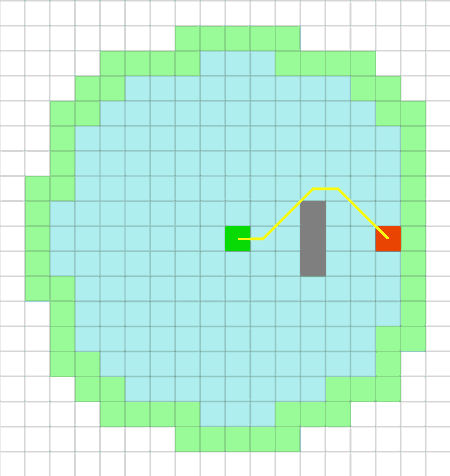
Рисунок 1 – Алгоритм Дейсктры
2.2 Алгоритм А*
Наилучшим алгоритмом для поиска оптимальных путей в различных пространствах является A* (читается как А-звездочка
) [2]. Этот эвристический поиск сортирует все узлы по приближению наилучшего маршрута идущего через этот узел. Типичная формула эвристики выражается в виде:
f(n) = g(n) + h(n),
где:
- f(n) значение оценки, назначенное узлу n;
- g(n) наименьшая стоимость прибытия в узел n из точки старта;
- h(n) эвристическое приближение стоимости пути к цели от узла n.
A* имеет множество интересных свойств. Он гарантированно находит кратчайший путь, до тех пор пока эвристическое приближение h(n) является допустимым, то есть он никогда не превышает действительного оставшегося расстояния до цели. Этот алгоритм наилучшим образом использует эвристику: ни один другой алгоритм не раскроет меньшее число узлов, не учитывая узлов с одинаковой стоимостью. На рисунке 2 показано как A* справляется с ситуацией проблемной для других алгоритмов.
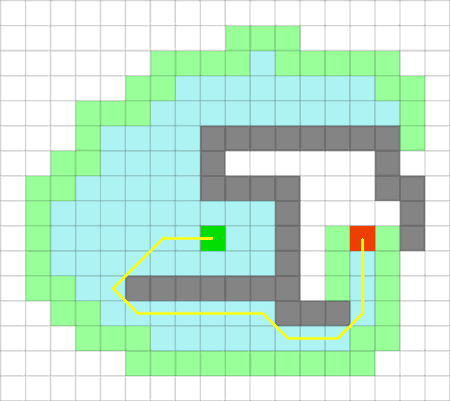
Рисунок 2 – Алгоритм А* в сложной ситуации
2.3 Алгоритм Jump Point Search (JPS)
Этот алгоритм является улучшенным алгоритмом поиска пути A*. JPS ускоряет поиск пути [3], перепрыгивая
многие места, которые должны быть просмотрены. В отличие от подобных алгоритмов JPS не требует предварительной обработки и дополнительных затрат памяти.
Алгоритм работает на неориентированном графе единой стоимости. Каждое поле карты имеет максимум 8 соседей, которые могут быть проходимы или же нет. Каждый шаг по направлению (по вертикали или по горизонтали) имеет стоимость 1; шаг по диагонали имеет стоимость v2. Движения через препятствия запрещены. Обозначение относится к одному из восьми направлений движения (вверх, вниз, влево и т.д.).
Прыжковые точки
позволяют ускорить алгоритм поиска пути, рассматривая только необходимые
точки. Такие точки могут быть описаны двумя простыми правилами выбора соседей при рекурсивном поиске: одно правило для прямолинейного движения и другое – для диагонального. В обоих случаях необходимо доказать, что исключая из набора ближайших соседей вокруг точки, найдётся оптимальный путь из предка текущей точки до каждого из соседей, и этот путь не будет содержать в себе посещенную точку. Пример работы алгоритма показан на рисунке 3.
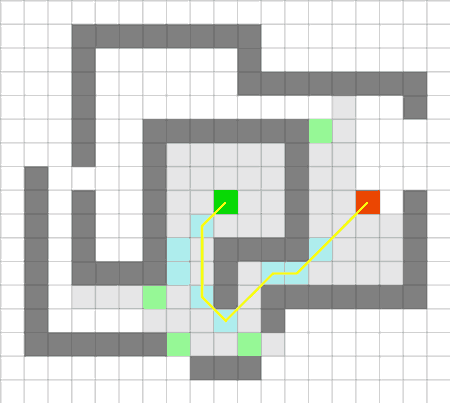
Рисунок 3 – Пример работы JPS
3. Методы локальных уклонений
В отличии от поиска пути, обход препятствий является динамической задачей, то есть требует расчета вектора скорости агентов в каждый момент времени t.
Существует несколько разных подходов к решению этой задачи. Самый простой подход – это поведения управления (Steering Behaviors) [4]. Этот подход включает в себя множество разных методик управления автономным агентом. Например, преследование, уклонение, трассировка пути, движение группой. Различные поведения агента показаны на рисунке 4.

Рисунок 4 – Поведения управления
Для решения задачи обхода движущихся препятствий необходимо скомбинировать преследование, уклонение и трассировку пути.
3.1 Скоростное препятствие
Скоростное препятствие для виртуального агента [5], созданное движущимся препятствием – это все векторы скоростей при движении по которым, через небольшой промежуток времени, произойдет коллизия между агентом и движущимся препятствием, при условии что препятствие будет двигаться с постоянной скоростью. Это означает, что если агент выберет себе вектор скорости, который находится в области скоростного препятствия, то, в будущем, между агентом и препятствием произойдет коллизия. Если скорость будет выбрана за пределами скоростного препятствия – коллизия не произойдет. Геометрическое представление скоростного препятствия VOab для агента А по отношению к агенту B, соответствующее конусу, показано на рисунке 5.
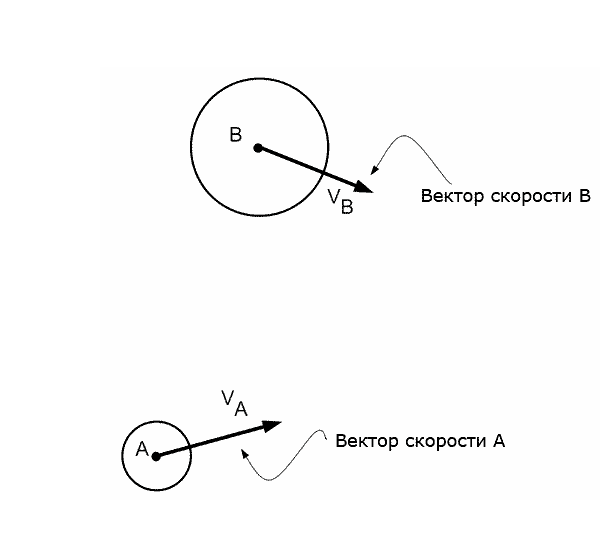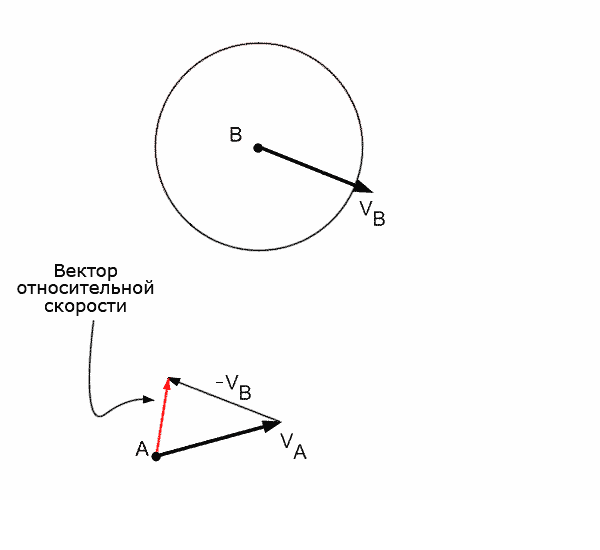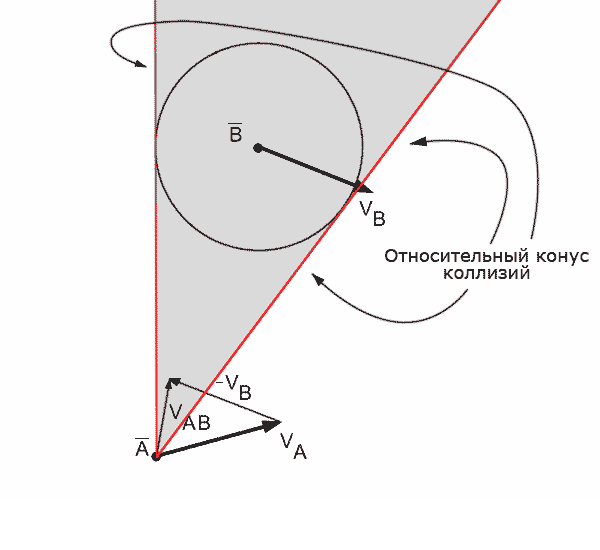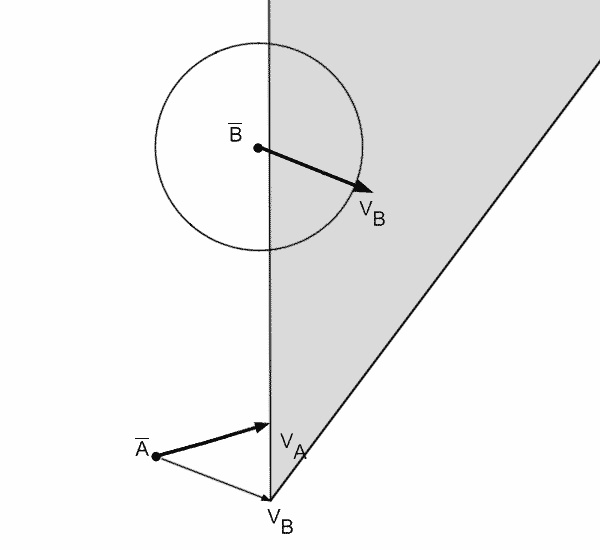
Рисунок 5 - Пример построения скоростного препятствия для агента А по отношению к агенту В (анимация: объем – 93,9 КБайт, количество кадров – 22, размер – 600 х 550)
Этот метод хорошо работает когда есть один виртуальный агент который движется в пространстве с большим количеством движущихся препятствий. Но, к сожалению, этот метод плохо работает на группе движущихся агентов, где каждый агент активно изменяет свой вектор скорости, для того, чтобы избежать коллизии, т.к. предполагает, что другие агенты не будут менять свою скорость. Это создает колебания в движении всех агентов.
3.2 Взаимное скоростное препятствие
Взаимное скоростное препятствие [6] направлено на решение проблемы колебаний, возникаемой при использовании скоростного препятствия, путем разрешения агентам реагировать на изменение вектора скорости другими агентами. Вместо того, что бы один из агентов брал на себя всю ответственность за совершение маневра уклонения, взаимное скоростное препятствие, позволяет агенту совершить лишь половину, допуская что вторую половину совершит другой агент. Геометрическое представление взаимного скоростного препятствия RVOab для виртуального агента А по отношению к агенту B, соответствующее скоростному препятствию с перемещенной вершиной, показано на рисунке 6.
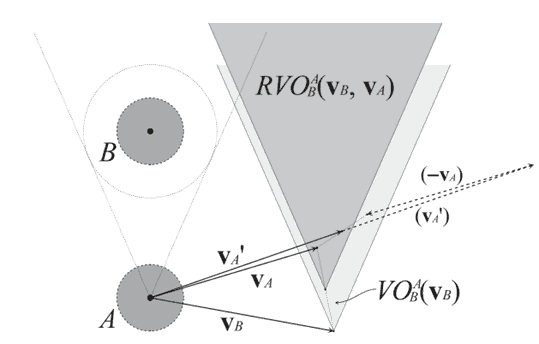
Рисунок 6 - Взаимное скоростное препятствие
Но и этот метод не идеален. У него существут ряд проблем, самой значимой из которых является проблема взаимных танцев
. Она проявляет себя тогда, когда агенты сильно отклоняются от намеченной тректории движения, вследствии чего могут оказаться заблокированными другими агенами. На решение этой проблемы направлены метод оптимальных взаимных скоростных препятствий [7] и метод гибридных взаимных скоростных препятствий [8].
4. Методы построения пути на навигационной поверхности
Навигационная поверхность – все проходимое пространство, состоящее из непересекающихся полигонов [9]. Навигационная поверхность может содержать дополнительную информацию. Например: стоимость прохода, или условия прохода для определенных классов юнитов. Строить пути по ней можно используя центра полигонов, грани, точки полигонов, либо несколько этих методов одновременно.
4.1 Перемещение по полигонам
Каждый центр полигона представляет собой вершину для графа поиска пути. На рисунке 7 показана навигационная поверхность с начальной и конечной точкой пути.
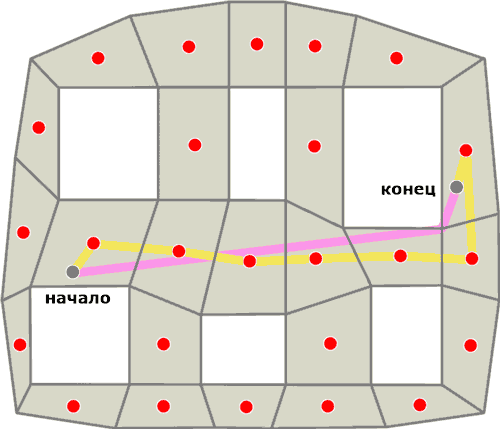
Рисунок 7 - Путь проложенный по центрам полигонов
Желтая линия – путь проложенный по центрам полигонов. Розовая – кратчайший путь. Этот подход дает далеко не самый короткий путь, но он один из самых простых.
4.2 Перемещения используя грани полигонов
Перемещение в центр полигона чаще всего не требуется. Поэтому этот подход дает гораздо лучший результат. На рисунке 8 показан пример. В качестве точек для перемещения выбраны центры граней. Но это не обязательно. Можно использовать несколько точек на грани. Этот подход дает более точный результат чем предыдущий, но путь все еще не самый короткий.
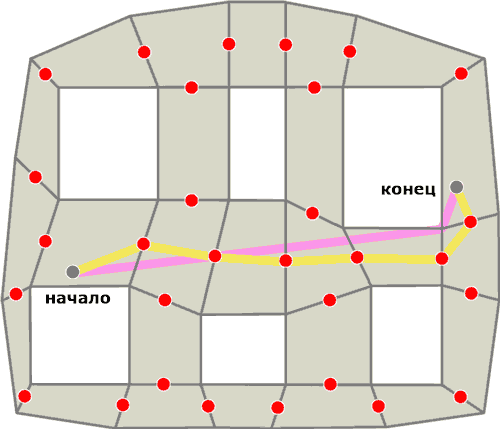
Рисунок 8 - Путь проложенный по центрам граней полигонов
4.3 Перемещение по точкам
Самый короткий путь вокруг препятствия – это его огибание. Этот принцип используется в данном методе. На рисунке 9 показан путь построенный по точкам полигонов.
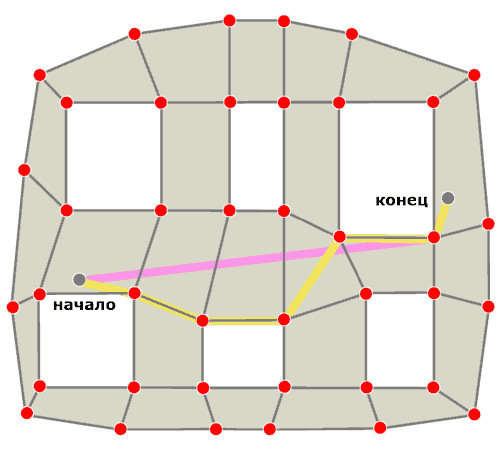
Рисунок 9 - Путь проложенный по точкам поверхности
Как видно из рисунка. На пути из начальной точки в конечную есть всего одно препятствие. Этот метод хорошо обогнул его, но движение вперёд выглядит не натурально и похоже больше на движение вдоль стены в лабиринте.
4.4 Гибридный метод
Выбор метода построения пути на навигационной поверхности ограничен только фантазией. Поэтому никто не запрещает использовать сразу несколько методов. Например на рисунке 10 показан путь построенный с помощью использования центров граней и точек полигонов.
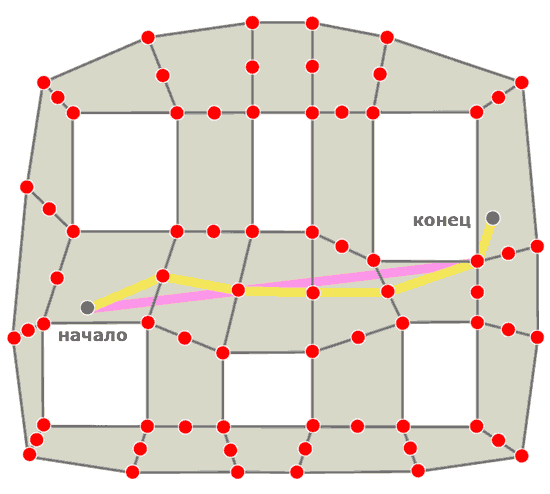
Рисунок 10 - Путь проложенный по точкам и центрам граней полигонов
Это позволило и эффективно обогнуть препятствие и достаточно естественно двигаться вперёд.
4.5 Сглаживание пути
Все вышеописанные методы дают неплохой результат, но он все равно не является самым коротким. Сглаживание позволяет избежать ненужных маневров и двигаться прямо к цели.
Метод прост: Если с навигационной точки i в точку i +2 существует прямой путь, но удалить точку i+1. Повторять это пока не останется точек которые можно удалить.
Этот простой метод позволит оставить только те навигационные точки, которые огибают препятствия. И если использовать сглаживание пути, то для начального построения пути нет необходимости использовать центры полигонов или грани. Достаточно использовать точки полигонов.
5. Решение проблем использования методов скоростных ограничений на навигационной поверхности
5.1 Обеспечение навигации вдоль проложенного маршрута и одновременный анализ возможных коллизий
Пусть кратчайший маршрут длинной N представляет собой последовательность точек:
 , (1)
, (1)
где  – начальная точка маршрута,
– начальная точка маршрута,
 – промежуточные точки маршрута,
– промежуточные точки маршрута,
 – конечная точка маршрута.
– конечная точка маршрута.
При перемещении по маршруту агент в каждый момент времени должен двигаться со скоростью:
 , (2)
, (2)
где i – индекс последней пройденной агентом точки маршрута,
 – величина скорости движения агента,
– величина скорости движения агента,
 – операция нормирования вектора.
– операция нормирования вектора.
Метод взаимных скоростных препятствий не учитывает данные о пункте назначения движения агента. Входными данными являются:
- требуемый вектор скорости для каждого из агентов (
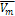 );
); - текущий вектор скорости каждого из агентов (
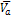 ).
).
Результатом применения метода является новый текущий вектор скорости для каждого из агентов. Очевидно, что для продолжения движения по намеченному маршруту, требуемый вектор скорости  необходимо пересчитывать в каждый момент времени:
необходимо пересчитывать в каждый момент времени:
 , (3)
, (3)
где 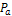 – текущая позиция агента на карте.
– текущая позиция агента на карте.
Описанная ситуация с векторами скоростей приведена на риcунке 11.
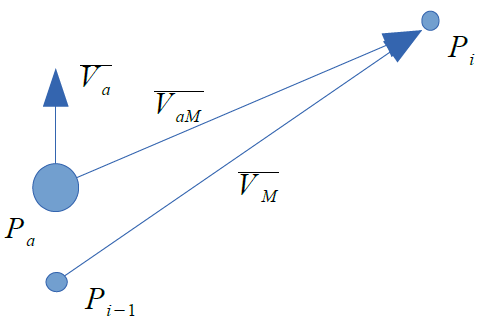
Рисунок 11 – Расчёт вектора скорости движения агента при совместном использовании методов поиска кратчайшего пути и метода взаимных скоростных ограничений для навигации по карте
5.2 Учёт ограничений на проходимость карты при расчёте локального уклонения
Маршрут M прокладывается таким образом, что движущийся по нему агент может касаться препятствий, но траектория его движения всегда находится в пределах проходимой области карты.
В то же время, при выполнении локального уклонения направление движения может быть выбран таким образом, что после выполнения маневра агент выйдет за границы области проходимости.
Метод взаимных скоростных препятствий позволяет рассчитать для агента вектор скорости, гарантирующий отсутствие столкновений с препятствиями. Таким образом, если представить границы областей проходимости на карте как препятствия для метода взаимных скоростных препятствий, то рассматриваемая проблема будет решена.
Каждый из полигонов навигационной поверхности можно разбить на непересекающиеся треугольники так, что их суммарная площадь будет равна площади полигона. Разбиение всех полигонов навигационной поверхности на треугольники будем называть триангуляцией навигационной поверхности. Пример навигационной поверхности и её триангуляции представлены на риcунке 12.
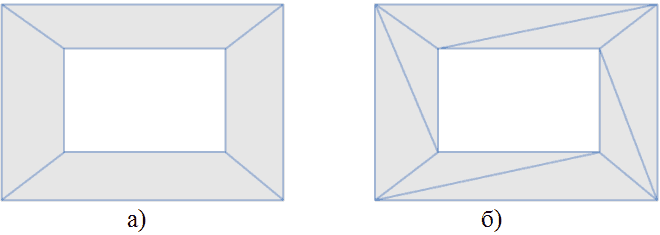
Рисунок 12 – Навигационная поверхность (а) и её триангуляция (б). Закрашенные области соответствуют проходимым участкам карты
Каждый из K полученных треугольников представляет собой полный граф. Если все эти треугольники объединить в один граф, то получим граф, состоящий K компонент связности. Если в этом графе объединить вершины, имеющие одинаковые координаты, то получим связный граф с кратными ребрами. Пусть в получившемся графе K вершин и пусть M – матрица смежности этого графа. Если над матрицей M выполнить следующую операцию
 , (4)
, (4)
то это будет соответствовать удалению в полученном графе всех кратных ребер. Полученный граф будет содержать только компоненты связности, каждая из которых будет циклом – контуром одной из границ непроходимых областей на карте.
5.3 Повторное прокладывание маршрута после выполнения локального уклонения
Одним из свойств маршрута, проложенного по навигационной поверхности, является то, что каждые две соседние точки в нем находятся в прямой видимости друг от друга, т.е. в контурах границ нет ребра, которое пересек бы отрезок  .
.
Как обсуждалось ранее, после выполнения локального уклонения вектор скорости агента к следующей точке пути будет нуждаться в пересчёте. Однако не исключено, что после уклонения в контурах границ найдётся ребро, с которым пересечется отрезок  . Наличие такого отрезка будем считать показателем необходимости повторного расчёта маршрута из точки
. Наличие такого отрезка будем считать показателем необходимости повторного расчёта маршрута из точки  в точку E.
в точку E.
Выводы
Магистерская работа посвящена решению актуальной научной задачи объединения методов поиска пути и локальных уклоений на навигационной поверхности. В рамках проведенных исследований выполнены следующие работы:
- Проведен анализ уже существующих методов поиска пути и локальных уклонений.
- Для выбранных методов и алгоритмов расмотрены возможности их совместного использования для решения поставленной задачи.
- Проведен ряд тестов и выявлены основные проблемы использования методов локальных уклонений на навигационной поверхности.
- Предложены возможности решения найденных проблем. Реализация этих решений позволит применять метод взаимных скоростных препятствий для обеспечения локальных уклонений агентов при следовании по маршруту по карте, представленной навигационной поверхностью.
Дальнейшие исследования направлены на следующие аспекты:
- Добавление приоритетов агентов в методы локального уклонения.
- Учет размеров агента при прокладывании маршрута по навигационной поверхности.
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2014 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список источников
- Алгоритм Дейкстры [Электронный ресурс] - Режим доступа: http://ru.wikipedia.org/wiki/Алгоритм_Дейкстры
- Алгоритм A* для новичков [Электронный ресурс] - Режим доступа: http://www.policyalmanac.org/games/aStarTutorial_rus.htm
- Harabor, D., Grastien, A.: Online Graph Pruning for Pathfinding on Grid Maps. In: Proceedings of the 25th National Conference on Artificial Intelligence (AAAI), San Francisco, USA (2011).
- C.W. Reynolds: Steering behaviors for autonomous characters - Game developers conference, 1999.
- P. Fiorini and Z. Shiller,
Motion planning in dynamic environments using velocity obstacles
, Int. Journal of Robotics Research, vol. 17, no. 7, pp. 760-772, 1998. - van den Berg, J., Lin, M., Manocha, D.: Reciprocal Velocity Obstacles for real-time multi-agent navigation. In: IEEE Int. Conf. on Robotics and Automation, pp. 1928–1935 (2008).
- J. Snape , J. van den Berg , S. J. Guy , D. Manocha, The Hybrid Reciprocal Velocity Obstacle, IEEE Transactions on Robotics, v.27 n.4, p. 696-706, August 2011
- van den Berg, J., Guy, S., Lin, M., Manocha, D. (2011). Reciprocal n-body collision avoidance. In C. Pradalier, R. Siegwart, G. Hirzinger (Eds.), Robotics Research: The 14th International Symposium ISRR (pp. 3-19). Berlin, Germany: Springer.
- Marcelo Kallmann, Shortest paths with arbitrary clearance from navigation meshes, Proceedings of the 2010 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, July 02-04, 2010, Madrid, Spain.
