Реферат за темою випускної роботи
Зміст
- 1. Постановка задачі
- 2. Актуальність теми дослідження
- 3. Мета та задачі
- 4. Існуючі підходи до виділення контурів зображень
- 4.1 Методи, які засновані на обчислені градієнта
- 4.2 Методи, які засновані на пошуку нулів
- 5. Запопонований метод
- Висновки
- Перелік посилань
1 Постановка задачі
Зображення можна визначити як двовимірну функцію f(x,y), де х та у – координати у просторі, і значення f якої в будь-якій точці, що задається парою координат (х,у) є інтенсивністю або рівнем сірого кольору в цій точці. Якщо величини x, y, f є кінцевими числами дискретних значень, то говорять про цифрове зображення. Цифровою обробкою зображень є обробка зображень за допомогою цифрових обчислювальних машин.
Цифрове зображеня складається з кінцевого числа елементів, які розташовуються в конкретному місці і приймає певне значення. Ці елементи називаються елементами зображення або пікселями [1].
Дослідженнями психологів встановлено, що з точки зору розпізнавання та аналізу об'єктів на зображенні найбільш інформативними є не значення яскравості об'єктів, а характеристики їх кордонів – контурів. Тож, основна інформація укладена не в яскравості окремих областей, а в їх обрисах. Завдання виділення контурів полягає в побудові зображення саме меж об'єктів і контурів однорідних областей.
Будемо називати контуром зображення сукупність пікселів, біля яких помічена стрибкоподібна зміна функції яскравості. Оскільки при цифровій обробці зображення представлено як функція цілочисельних аргументів, то контури представляються лініями шириною, як мінімум, в один піксель [2].
Вихідним даним даної задачі є зображення, яке представлено набором пікселів. Кожен піксель характеризується значенням яскравості у заданому діапазоні. Результатом – набір пікселів, які задають контури зображення.
Тож, необхідно розробити алгоритм виділення контурів зображення. Оскільки зорово-аналізуюча система людини досить ефективно і оперативно справляється з цим завданням за рахунок своїй надзвичайно високій вибірковості, потрібно при розробці алгоритму врахувати механізм зорового аналізатора людини, виходячи із будови та принципів роботи зорової системи [3, 4].
2. Актуальність теми дослідження
Основна ідея даної роботи – це виділення контурів об’єктів зображення. Ця задача зустрічається в багатьох аспектах сучасного життя: на виробництвах, в обробці візуальної інформації, у медичній діагностиці тощо. Тому розв’язання подібної задачі – це актуальне питання.
На сьогоднішній день існують методи, які вирішують такі питання. Однак, оскільки в цифровій обробці зображення задається матрицею відповідних пікселів і не всі з них несуть корисну інформацію, тож виникає проблема раціонального використання ресурсів. Тож необхідний метод, який відфільтровує без інформативну частину зображення (у вигляді пікселів) та концентрується на корисній інформації. Прикладом подібної обробки даних – є сприйняття людиною візуальної інформації. Тому метою даної роботи – є розробка алгоритму, який засновано на зорово-аналітичному механізмі людини.
3. Мета та задачі
Мета даної роботи – це розробка алгоритму, що засновано на зорово-аналітичному механізмі людини.
Основні задачі дослідження:
- вивчити та проаналізувати існуючи підходи до виділення контурів об’єктів зображення;
- розглянути зоровий механізм людини;
- розробити та реалізувати алгоритм виділення контурів зображення на основі сприйняття світла сітківкою ока людини.
Об’єкт дослідження: процес виділення контурів зображення алгоритмом, який базується на механізмі сприйняття світла сітківкою ока людини.
Предмет дослідження: контури об'єктів зображення.
4. Існуючі підходи до виділення контурів зображень
Виділення контурів зображень – термін в теорії обробки зображення і комп'ютерного зору, частково з області пошуку об'єктів і виділення об'єктів, ґрунтується на алгоритмах, які виділяють точки цифрового зображення, в яких різко змінюється яскравість або є інші види неоднорідностей.
В ідеальному випадку, результатом виділення контурів є набір пов'язаних кривих, що позначають межі об'єктів, граней і відбитків на поверхні, а також криві які відображають зміни положення поверхонь. Таким чином, застосування фільтра виділення кордонів до зображення може істотно зменшити кількість оброблюваних даних, через те, що відфільтрована частина зображення вважається менш значущою, а найбільш важливі структурні властивості зображення зберігаються.
Однак не завжди можливо виділити контур в картинах реального світу середньої складності. Межі виділені з таких зображень часто мають такі недоліки як фрагментованість (криві контурів не з'єднані між собою), відсутність меж або наявність помилкових, які не відповідають досліджуваному об'єкту.
Існує безліч підходів до виділення контурів зображень, але майже всі можна поділити на дві категорії: методи, що засновані на пошуку максимумів, і методи, що засновані на пошуку нулів.
Методи, що засновані на пошуку максимумів, виділяють контури за допомогою обчислення "сили краю", зазвичай вирази першої похідної, такого як величина градієнта, і потім пошуку локальних максимумів сили краю, використовуючи передбачуваний напрямок контуру, зазвичай перпендикуляр до вектора градієнта. Методи, які засновані на пошуку нулів, шукають перетину осі абсцис виразу другої похідної, зазвичай нулі Лапласіан або нулі нелінійного диференціального виразу. В якості кроку попередньої обробки до виділення кордонів практично завжди застосовується згладжування зображення, зазвичай фільтром Гаусса.
Методи виділення контурів відрізняються застосовуваними фільтрами згладжування. Хоча багато методів виділення кордонів ґрунтуються на обчисленні градієнта зображення, вони відрізняються типами фільтрів, що застосовуються для обчислення градієнтів в x- та y–напрямках [5].
4.1 Методи, які засновані на обчислені градієнта.
Більшість методів, які застосовують для виділення контурів зображень засновані на обчисленні градієнта зображення. Нагадаємо, що градієнт визначається, як векторна величина, що показує напрямок найшвидшого зростання деякої величини. Де в даному випадку величиною є двовимірна функція яскравості зображення.
(1.1)

У формулі 1.1 I – це вихідне зображення.
Найбільш відомими операторами цього класу методів є оператори Собеля, Превітта та Робертса.
Усі зазначені методи ґрунтуються на одної з базових властивостей сигналу яскравості – розривності. Найбільш загальним способом пошуку розривів є обробка зображення за допомогою ковзної маски, званої також фільтром, ядром, вікном або шаблоном, яка являє собою якусь квадратну матрицю, що відповідає зазначеній групі пікселів вихідного зображення. Елементи матриці прийнято називати коефіцієнтами. Оперування такою матрицею в будь-яких локальних перетвореннях називається фільтрацією або просторової фільтрацією. На наступному зображені представлено загальну схему просторової фільтрації [6].
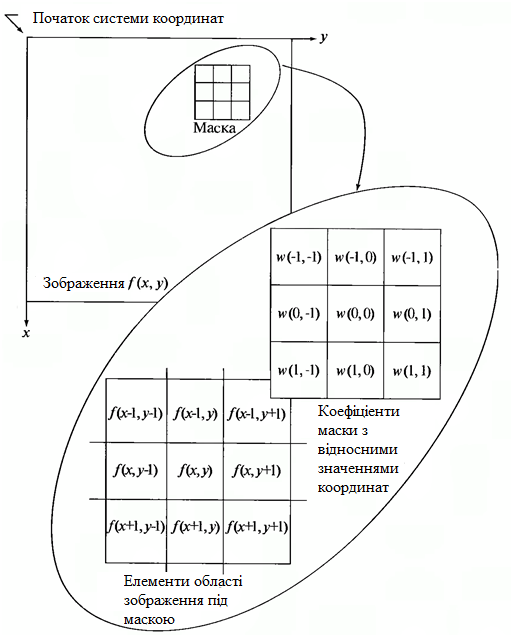
Рисунок 1 – Схема просторової фільтрації
Процес заснований на простому переміщенні маски фільтра від точки до точки зображення; в кожній точці (x, y) відгук фільтра обчислюється з використанням попередньо заданих зв'язків. У разі лінійної просторової фільтрації відгук задається сумою добутку коефіцієнтів фільтра на відповідні значення пікселів в області, що покрита маскою фільтра. Для маски 3х3 елемента, показаної на рисунку 1.1, результат (відгук) R лінійної фільтрації в точці (x, y) зображення складе (див. формулу 1.2):
(1.2)

З даної формули можна побачити,що отримуємо суму додатку коефіцієнтів маски на значення пікселів відповідно до маски. Коефіцієнт w(0,0) відповідає значенню f(x,y), що вказує на відцентрування маски до точки (х,у). При виявленні перепадів яскравості використовуються дискретні аналоги похідних першого і другого порядку. Перша похідна одновимірної функції f(x) визначається як різниця значень сусідніх елементів.
(1.3)

Аналогічно, друга похідна визначається як різниця сусідніх значень першої похідної:
(1.4)

Обчислення першої похідної цифрового зображення засновано на різних дискретних наближеннях двовимірного градієнта. За визначенням, градієнт зображення f(x, y) в точці (x, y) – це вектор [7]:
(1.5)

Важливу роль при виявленні контурів грає модуль цього вектора, який позначається ∇f і дорівнює:
(1.6)

Ця величина дорівнює значенню максимальної швидкості зміни функції f в точці (x, y), де максимум досягається в напрямку вектора ∇ f. Величину ∇ f також часто називають градієнтом. Напрямок вектора градієнта також є важливою характеристикою. Позначимо α(x, y) кут між напрямком вектора ∇ f в точці (x, y) і віссю x. Як відомо з математичного аналізу [7]:
(1.7)

Звідси легко знайти напрям контуру в точці (x, y), який є перпендикулярним напрямку вектора градієнта в цій точці.
А знайти градієнт зображення можна, обчисливши величини приватних похідних и
и  для кожної точки.
для кожної точки.
4.2 Методи, які засновані на пошуку нулів.
Деякі оператори виділення кордонів замість роботи з градієнтом використовують другі похідні яскравості зображення. Це природним чином визначає силу зміни градієнта. Таким чином, в ідеальному випадку, виявлення нулів другої похідної дозволить виявити локальні максимуми градієнта.
Оператор Марра-Хілдрет заснований на обчислення коренів оператора Лапласа, застосованого до зображення, згладженому фільтром Гаусса. Однак, було показано, що цей оператор виділяє помилкові кордони на однорідних ділянках зображення, де градієнт має локальний мінімум. До того ж цим оператором погано локалізовалися округлені краї. Тому даний оператор представляє зараз скоріше історичну цінність. Более актуальный способ выделения контуров второго порядка, который так же выделяет контур с пиксельной точностью, – использование следующего дифференциального подхода к выявлению нулей второй производной по направлению вектора градиента. Більш актуальний спосіб виділення контурів другого порядку, який так само виділяє контур з піксельной точністю, – використання наступного диференціального підходу до виявлення нулів другої похідної за напрямом вектора градієнта [8]. Введемо в кожній точці зображення локальну систему координат (u, v), де v – напрям паралельно градієнту. Припускаючи, що зображення було згладжено фільтром Гаусса, і масштабне уявлення L(x, y; t) на масштабі t було пораховано, ми можемо вимагати, щоб величина градієнта масштабного подання, яке дорівнює першої похідної за напрямом Lv в v-напрямку , буде мати першу похідну в v-напрямку, рівну нулю:
(1.8)

в той час як друга похідна в v-напрямку від Lv повинна бути від’ємною, оскільки нас цікавлять тільки максимуми, тобто:
(1.9)

Записане в якості явного виразу від локальних приватних похідних Lx, Ly... Lyyy, дане визначення краю може бути виражене в якості нульових ліній диференціального інваріанта
(1.10)

який задовольняє такій умові:
(1.11)

де Lx, Ly... Lyyy позначають приватні похідні пораховані на масштабному поданні L, отриманому за допомогою фільтрації вихідного зображення фільтром Гаусса.
У даному випадку краї будуть автоматично представляти собою безперервні криві з пиксельною точністю. До отриманих країв може бути додатково застосовано виділення за допомогою порогів із запізненням [5].
На практиці, перші похідні можуть бути пораховані як описувалося раніше, в той час як другі похідні можуть бути обчислені з масштабного подання L так:
(1.12)

Це відповідає наступним операторам:
(1.13)
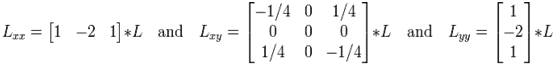
5. Запропанований метод
Розіб’ємо розв'язання задачі на окремі етапи. Кожен з етапів відповідає окремій функції. Розглянемо послідовність виконання кожного етапу далі. Тож, ми маємо вихідне зображення I розміром NxM пікселів, що задано матрицею характеристик яскравості. Зображення потрапляє до роботи системи, що є аналогом людського сприйняття, де зображення потрапляє на сітківку ока людини. Кожен піксель зображення відповідає фоторецептору на центральній ямці сітківки. Далі послідовно аналізуємо кожен піксель і оточуючи його пікселі, з точки зору їх яскравості (див. рис. 2). Ця процедура базується на механізмі роботи фоторецепторних клітин [9]. Це – перший етап розпізнавання контурів.
Рисунок 2 – Пікселі, що аналізуються на характеристику яскравості
На рисунку 2 i0 – яскравість аналізуємогопікселя; i1, i2, i3, i4 – яскравість оточуючих пікселів.
Наступним кроком є аналіз на горизонтальному шарі клітин, де розглядаються сигнали від сусідніх пікселів.
Після цього результати попередніх етапів потрапляють на аналог біполярних клітин запропонованого алгоритму. Тут порівнюється яскравість пікселя із заданим значенням. Результати порівняння визначають належність пікселя до відповідного рецептивного поля. А саме, якщо яскравість пікселяменьша від опорного значення, тоді піксель відноситься до рецептивного поля з off-центром. Інакше – з on-центом. Цей показник грунтується на сигналі освітленя або затемнення відповідно [10, 11].
Таким чином ми отримали шар біполярних клітин.Далі, виходячи із отриманого результату, аналізуються пікселі, що належать до амакриного шару, які задають гангліозну клітину пікселя, що розглядається.
Кінцевим етапом є порівняння вихідного пікселя із параметром, який варіюється залежно від початкового зображення. Даний параметр є середнім значенням яскравості пікселівсьго зображення. Отже, ми отримаємо чи належить аналізуємийпіксель до контуру зображення, чи – до самого об‘єкта. На наступному рисунку схематично наведено запропонований алгоритм.
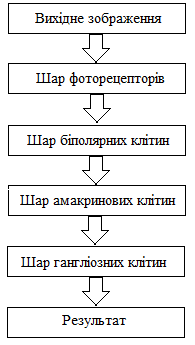
Рисунок 3 – Схема послідовності шарів сітківки для розпізнавання контурів зображень

Рисунок 4 – Процес виділення контурів зображення
(анімация: 7 кадрів, 7 циклів повторення, 36 кілобайт)
Висновки
Проведено аналіз методів виділення контурів об’єктів зображення. Розглянуто підхід, який засновано на механізмі сприйняття світла сітківкою ока людини. Вважається, що попередня обробка світового сигналу (який формує зображення) відбувається у сітківці людини. В основі запропонованого методу – моделювання основних шарів сітківки людини (шари фоторецепторів, беполярних клітин, амакриних клітин та гангліозних клітин). В подальшому планується реалізувати ці шари за допомогою нейронних мереж.
Примітка
На етапі написання даного реферату магістерська робота знаходилася на етапі розробки. Повний текст роботи буде готовий до лютого 2015 року.
Перелік посилань
- Гонсалес Р. С., Вудс Р. Э. Цифровая обработка изображений. - М.: Техносфера, 2006. - 1072 с.
- Сойфер В. А. Компьютерная обработка изображений. - М.: Физматлит, 1996. - 784 с.
- Боюн В.П. Зоровий аналізатор людини як прототип для побудови сімейства проблемно-орієнтованих систем технічного зору /В.П. Боюн // Материалы Международной научно-технической конференции «Искусственный интеллект. Интеллектуальные системы. ИИ-2010». – 2010.Т.1. – С. 21-26.
- Boycott B.B. Organization of the Primate Retina: Light Microscopy / B.B. Boycott, J.E. Dowling// Philosophical Transaction of the Royal Society of London. – Series B, Biological Sciences. – vol. 255, is.799. – 1969. – P.109-184.
- RamadeviY., SrideviT., PoornimaB. SegmentationandObjectRecognitionusingEdgeDetectionTechniques / Y.Ramadevi, T. Sridevi, B. Poornima, B. Kalyani // Internation Journal of Computer Scienceand Information Technology. – 2010. – vol.2, No 6. – P.153-161.
- Алгоритмы выделения контуров зображений // [Електронный ресурс] – код доступу: http: //habrahabr.ru/post/114452/
- Кудрявцев Л.В. Краткий курс математического анализа – M.: Наука, 1989 – 736с
- Differential Operators for Edge Detection // [Електронный ресурс] – код доступу: http://dspace.mit.edu/bitstream/handle/1721.1/41198/ai_wp_252.pdf?sequence=4
- Сетчатка //Электронный журнал «Биология и медицина». // [Електронный ресурс] – код доступу: http:// http://medbiol.ru/medbiol/phus_ner/0008db2b.htm#0004a91e.htm
- Вовк О.Л. Учет особенностей строения сетчатки глаза человека для выделения контуров объектов изображений / О.Л. Вовк // Наукові праці Донецького національного технічного університету: “Інформатика, кібернетика та обчислювальна техніка”. – ДНТУ, Донецьк. – 2013. – Випуск 17 (205). – С.48-52.
- Golish T. Eye Smarter than Scientists Believed: Neural Computations in Circuits of the Retina / T. Golish, M. Meister //Neuron. – vol.65, IS.2. – 2010. – P.150-164
