ДонНТУ   Портал магистров

Витковская Екатерина Викторовна

Факультет компьютерных наук и технологий

Кафедра прикладной информатики и математики

Специальность «Инженерия программного обеспечения»

Выделение контуров объектов изображения с использованием аппарата восприятия света сетчаткой глаза человека

Научный руководитель: д.т.н., доц. Вовк Ольга Леонидовна

Резюме Биография Реферат Библиотека Ссылки Отчет о поиске Индивидуальный раздел

Реферат по теме выпускной работы

Содержание

• 1. Постановка задачи
• 2. Актуальность темы
• 3. Цель и задачи исследования
• 4. Обзор существующих методов выделения контуров изображения
• 4.1 Методы, которые основаны на вычисление градиента
• 4.2 Методы, основанные на поиске нулей
• 5. Предлагаемый метод
• Выводы
• Список источников

1. Постановка задачи

Изображение можно определить как двумерную функцию f(x, y), где х и у – координаты в пространстве, и значение f которой в любой точке, задается парой координат (х, у) является интенсивностью или уровнем серого цвета в этой точке. Если величины x, y, f являются конечными числами дискретных значений, то говорят о цифровом изображении.

Цифровой обработкой изображений является обработка изображений с помощью цифровых вычислительных машин. Цифровые изображения состоят из конечного числа элементов, которые располагаются в конкретной позиции и принимают определенное значение. Эти элементы называются частями изображения или пикселями [1].

Исследованиями психологов установлено, что с точки зрения распознавания и анализа объектов на изображении наиболее информативными является не значение яркости объектов, а характеристики их границ – контуров. Поэтому, основная информация заключена не в яркости отдельных областей, а в их очертаниях. Задача выделения контуров состоит в построении изображения именно границ объектов и контуров однородных областей.

Будем называть контуром изображения совокупность пикселей, у которых замечена скачкообразное изменение функции яркости. Поскольку при цифровой обработке изображения представлены как функция целочисленных аргументов, то контуры представляются линиями шириной, как минимум, в один пиксель [2].

Исходным данным данной задачи является изображение, которое представлено набором точек. Каждый пиксель характеризуется значением яркости в заданном диапазоне. Результатом – набор точек, которые задают контуры изображения.

Исходя из этого, необходимо разработать алгоритм выделения контуров изображения. Поскольку зрительно – анализирующая система человека достаточно эффективно и оперативно справляется с этой задачей за счет своей чрезвычайно высокой избирательности, нужно при разработке алгоритма учесть механизм зрительного анализатора человека, исходя из строения и принципов работы зрительной системы [3, 4].

2. Актуальность темы

Основная идея данной работы – это выделение контуров объектов изображения. Эта задача встречается во многих аспектах современной жизни: на производствах, в обработке визуальной информации, в медицинской диагностике и т.д. Поэтому решение подобной задачи – это актуальный вопрос. На сегодняшний день существуют методы, которые решают такие вопросы.

Однако, поскольку в цифровой обработке изображения задается матрицей соответствующих точек и не все из них несут полезную информацию, поэтому возникает проблема рационального использования ресурсов. Поэтому необходим метод, который отфильтровывает безинформативную часть изображения (в виде точек) и концентрируется на полезной информации. Примером подобной обработки данных – восприятие человеком визуальной информации. Поэтому целью данной работы – является разработка алгоритма, основанного на зрительно-аналитическом механизме человека.

3. Цель и задачи исследования

Цель данной работы – это разработка алгоритма, основанного на зрительно-аналитическом механизме человека.

Основные задачи исследования:

1. изучить и проанализировать существующие подходы к выделению контуров объектов изображения;
2. рассмотреть и изучить зрительный механизм человека;
3. разаботать и реализовать алгоритм выделения контуов изобажения на основе восприятия света сетчаткой глаза человека.

Объект исследования: процесс выделения контуров изображения алгоритмом, который базируется на механизме восприятия света сетчаткой глаза человека.

Предмет исследования: контуры объектов изображения.

4. Обзор существующих методов выделения контуров изображения

Выделение контуров изображений – определение в теории обработки изображения и компьютерного зрения, частично из области поиска объектов и выделения объектов, основывается на алгоритмах, которые выделяют точки цифрового изображения, в которых резко меняется яркость или есть другие виды неоднородностей.

В идеальном случае, результатом выделения контуров является набор связанных кривых, обозначающих границы объектов, граней и отпечатков на поверхности, а также кривые отражающие изменения положения поверхностей. Таким образом, применение фильтра выделения границ к изображению может существенно уменьшить количество обрабатываемых данных, из-за того, что отфильтрованная часть изображения считается менее значимым, а наиболее важные структурные свойства изображения сохраняются.

Однако не всегда возможно выделить контур в картинах реального мира средней сложности. Границы выделены из таких изображений часто имеют такие недостатки как фрагментированность (кривые контуров отсутствует соединение между собой), отсутствие границ или наличие ложных, не соответствующих изучаемому объекту.

Существует множество подходов к выделению контуров изображений, но почти все можно разделить на две категории: методы, основанные на поиске максимумов, и методы, основанные на поиске нулей.

Методы, основанные на поиске максимумов, выделяют контуры с помощью вычисления «силы края», обычно выражения первой производной, такого как величина градиента, и затем поиска локальных максимумов силы края, используя предполагаемое направление контура, обычно перпендикуляр к вектору градиента.

Методы, основанные на поиске нулей, ищут пересечения оси абсцисс выражения второй производной, обычно нули Лапласиан или нули нелинейного дифференциального выражения. В качестве шага предварительной обработки к выделению границ практически всегда применяется сглаживание изображения, обычно фильтром Гаусса. Методы выделения контуров отличаются применяемыми фильтрами сглаживания. Хотя много методов выделения границ основываются на вычислении градиента изображения, они отличаются типами фильтров, применяемых для вычисления градиентов в x- и y-направлениях [5].

4.1 Методы, основанные на вычисление градиента

Большинство методов, которые применяют для выделения контуров изображений основаны на вычислении градиента изображения. Напомним, что градиент определяется, как векторная величина, показывающая направление наискорейшего роста некоторой величины. Где в данном случае величиной является двумерная функция яркости изображения.

В формуле 1.1 I – это исходное изображение.

Наиболее известными операторами этого класса методов являются операторы Собеля, Прюитта и Робертса.

Все указанные методы основываются на одной из базовых свойств сигнала яркости – разрывности. Наиболее общим способом поиска разрывов является обработка изображения с помощью скользящей маски, называемой также фильтром, ядром, окном или шаблоном, которая представляет собой некую квадратную матрицу, соответствующую указанной группе пикселей исходного изображения. Элементы матрицы принято называть коэффициентами. Оперирование такой матрицей в любых локальных преобразованиях называется фильтрацией или пространственной фильтрацией. На следующем изображение представлена общая схема пространственной фильтрации [6].

Процесс основан на простом перемещении маски фильтра от точки до точки изображения; в каждой точке (x, y) отклик фильтра вычисляется с использованием предварительно заданных связей. В случае линейной пространственной фильтрации отзыв задается суммой произведения коэффициентов фильтра на соответствующие значения пикселей в области, покрытой маской фильтра. Для маски 3х3 элемента, показанной на рисунке 1, результат (отклик) R линейной фильтрации в точке (x, y) изображения составит (см. формулу 1.2):

Из данной формулы можно увидеть, что получаем сумму приложении коэффициентов маски на значения пикселей в соответствии с маски. Коэффициент w(0,0) соответствует значению f(x, y), что указывает на маска центрирована в точке (х, у). При обнаружении перепадов яркости используются дискретные аналоги производных первого и второго порядка. Первая производная одномерной функции f(x) определяется как разница значений соседних элементов.

Аналогично, вторая производная определяется как разность соседних значений первой производной:

Вычисление первой производной цифрового изображения основано на различных дискретных приближениях двумерного градиента. По определению, градиент изображения f(x, y) в точке (x, y) – это вектор [7]:

Важную роль при выявлении контуров играет модуль этого вектора, который обозначается ∇f и равен:

Эта величина равна значению максимальной скорости изменения функции f в точке (x, y), где максимум достигается в направлении вектора ∇f. Величину ∇f также часто называют градиентом.

Направление вектора градиента также является важной характеристикой. Обозначим α(x, y) угол между направлением вектора ∇f в точке (x, y) и осью x. Как известно из математического анализа [7]:

Эта величина равна значению максимальной скорости изменения функции f в точке (x, y), где максимум достигается в направлении вектора ∇f. Величину ∇f также часто называют градиентом. Отсюда легко найти направление контура в точке (x, y), который является перпендикулярным направлению вектора градиента в этой точке. А найти градиент изображения можно, вычислив величины частных производных и для каждой точки.

4.2 Методы, основанные на поиске нулей.

Некоторые операторы выделения границ вместо работы с градиентом используют вторые производные яркости изображения. Это естественным образом определяет силу изменения градиента. Таким образом, в идеальном случае, выявления нулей второй производной позволит выявить локальные максимумы градиента.

Оператор Марра-Хилдрет основан на вычисление корней оператора Лапласа, примененного к изображению, сглаженного фильтром Гаусса. Однако, было показано, что этот оператор выделяет ложные границы на однородных участках изображения, где градиент имеет локальный минимум. К тому же этим оператором плохо локализовались скругленные края. Поэтому данный оператор представляет сейчас скорее историческую ценность. Более актуальный способ выделения контуров второго порядка, который так же выделяет контур с пиксельной точностью, – использование следующего дифференциального подхода к выявлению нулей второй производной по направлению вектора градиента [8]. Введем в каждой точке изображения локальную систему координат (u, v), где v – направление параллельно градиенту. Предполагая, что изображение было сглажено фильтром Гаусса, и масштабное представление L (x, y; t) на масштабе t было сочтено, мы можем требовать, чтобы величина градиента масштабного представления, равное первой производной по направлению L_v в v-направлении, будет иметь первую производную в v-направлении, равную нулю:

в то время как вторая производная в v- направлении от L_v должна быть отрицательной, поскольку нас интересуют только максимумы, т.е.:

Записанное в качестве явного выражения от локальных частных производных L_x, L_y... L_yyy, данное определение края может быть выражено в качестве нулевых линий дифференциального инварианта

удовлетворяющего следующему условию:

где L_x, L_y... L_yyy обозначают частные производные посчитаны на масштабном представлении L, полученном с помощью фильтрации исходного изображения фильтром Гаусса. В данном случае края будут автоматически представлять собой непрерывные кривые с пиксельной точностью. К полученным краям может быть дополнительно применено выделение с помощью порогов с опозданием [5]. На практике, первые производные могут быть расчитаны как описывалось ранее, в то время как вторые производные могут быть вычислены с масштабным представлением L так:

Это соответствует следующим операторам:

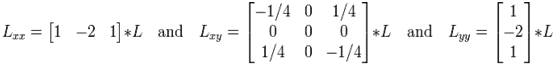
5. Предлагаемый метод

Разобьем решение задачи на отдельные этапы. Каждый из этапов соответствует отдельной функции. Рассмотрим последовательность выполнения каждого этапа дальше. Таким образом, мы имеем исходное изображение I размером NxM пикселей, что задано матрицей яркостных. Изображение попадает к работе системы, является аналогом человеческого восприятия, где изображение попадает на сетчатку глаза человека. Каждый пиксель изображения соответствует фоторецепторам на центральной ямке сетчатки. Далее последовательно анализируем каждый пиксель и окружающие его пиксели, с точки зрения их яркости (см. рис. 2). Эта процедура основана на механизме работы фоторецепторных клеток [9]. Это – первый этап распознавания контуров.

На рисунке 2 i₀ – яркость анализируемого пикселя; i₁, i₂, i₃, i₄ – яркость окружающих пикселей.

Следующим шагом является анализ на горизонтальном слое клеток, где рассматриваются сигналы от соседних пикселей.

После этого результаты предыдущих этапов попадают в аналог биполярных клеток предложенного алгоритма. Здесь сравнивается яркость пикселя с заданным значением. Результаты сравнения определяют принадлежность пикселя к соответствующему рецептивного поля. А именно, если яркость пикселя меньше чем заданное значение, тогда пиксель относится к рецептивному полю off-центром. Иначе – с on-центом. Этот показатель основывается на сигнале освещения или затемнения соответственно [10, 11].

Таким образом, мы получили слой биполярных клеток. Далее, исходя из полученного результата, анализируются пиксели, принадлежащие к амакриному слою, которые задают ганглиозные клетки пикселя, которые рассматривается.

Конечным этапом является сравнение исходного пикселя с параметром, который варьируется в зависимости от исходного изображения. Данный параметр является средним значением яркости пикселя всего изображения. Итак, мы получим принадлежит анализируемый пиксель к контуру изображения, или – к самому объекту. На следующем рисунке схематически приведен предложенный алгоритм.

Выводы

Проведен анализ методов выделения контуров объектов изображения. Рассмотрен подход, основанный на механизме восприятия света сетчаткой глаза человека. Считается, что предварительная обработка мирового сигнала (который формирует изображение) происходит в сетчатке человека. В основе предложенного метода – моделирование основных слоев сетчатки человека (слои фоторецепторов, биполярных клеток, амакриных клеток и ганглиозных клеток). В дальнейшем планируется реализовать эти слои с помощью нейронных сетей.

Примечание

На этапе написания данного реферата магистерская работа находилась на этапе разработке. Полный текст работы будет готов к февралю 2015 года.

Список источников

1. Гонсалес Р. С., Вудс Р. Э. Цифровая обработка изображений. - М.: Техносфера, 2006. - 1072 с.
2. Сойфер В. А. Компьютерная обработка изображений. - М.: Физматлит, 1996. - 784 с.
3. Боюн В.П. Зоровий аналізатор людини як прототип для побудови сімейства проблемно-орієнтованих систем технічного зору /В.П. Боюн // Материалы Международной научно-технической конференции «Искусственный интеллект. Интеллектуальные системы. ИИ-2010». – 2010.Т.1. – С. 21-26.
4. Boycott B.B. Organization of the Primate Retina: Light Microscopy / B.B. Boycott, J.E. Dowling// Philosophical Transaction of the Royal Society of London. – Series B, Biological Sciences. – vol. 255, is.799. – 1969. – P.109-184.
5. RamadeviY., SrideviT., PoornimaB. SegmentationandObjectRecognitionusingEdgeDetectionTechniques / Y.Ramadevi, T. Sridevi, B. Poornima, B. Kalyani // Internation Journal of Computer Scienceand Information Technology. – 2010. – vol.2, No 6. – P.153-161.
6. Алгоритмы выделения контуров зображений // [Электронный ресурс] – код доступа: http: //habrahabr.ru/post/114452/
7. Кудрявцев Л.В. Краткий курс математического анализа – M.: Наука, 1989 – 736с
8. Differential Operators for Edge Detection // [Электронный ресурс] – код доступа: http://dspace.mit.edu/bitstream/handle/1721.1/41198/ai_wp_252.pdf?sequence=4
9. Сетчатка //Электронный журнал «Биология и медицина». // [Электронный ресурс] – код доступа: http:// http://medbiol.ru/medbiol/phus_ner/0008db2b.htm#0004a91e.htm
10. Вовк О.Л. Учет особенностей строения сетчатки глаза человека для выделения контуров объектов изображений / О.Л. Вовк // Наукові праці Донецького національного технічного університету: “Інформатика, кібернетика та обчислювальна техніка”. – ДНТУ, Донецьк. – 2013. – Випуск 17 (205). – С.48-52.
11. Golish T. Eye Smarter than Scientists Believed: Neural Computations in Circuits of the Retina / T. Golish, M. Meister //Neuron. – vol.65, IS.2. – 2010. – P.150-164