RU   EN
ДонНТУ   Портал магістрів

Реферат за темою випускної роботи

Зміст

Вступ

САПР, або системи автоматизованого проектування - це цифрові платформи, створені для підвищення ефективності праці інженерів, оскільки в наш час мало хто віддає перевагу паперові креслення електронним. Вони знаходять широке застосування практично в багатьох сферах виробничої та будівельної діяльності.

У наш час комп'ютерні технології бурхливо розвиваються, і комплекси САПР отримують все більш якісні можливості для дизайну об'єктів і їх моделювання в умовах фізичних та температурних навантажень, а також розрахунку аеро - і гідродинаміки проектованих моделей. Таким чином, поліпшення точності моделювання є однією з головних завдань модернізації САПР.

1. Актуальність теми

Комплекси САПР розбиті на підсистеми, і тією, яка відповідає за моделювання об'єктів, є CAE - Computer-Aided Engineering. CAE представляє з себе комплекс програмних продуктів, які можуть дати користувачеві характеристику того, як в реальності буде вести себе розроблена на комп'ютері модель виробу. За допомогою CAE інженер може досить точно оцінити працездатність виробу, не вдаючись при цьому до значних тимчасових і грошових витрат. У своїй роботі CAE використовують різні математичні розрахунки: метод кінцевих елементів, метод кінцевих обсягів, метод кінцевих різниць.

Найчастіше буває, що надмірна точність використовуваних математичних розрахунків може бути причиною помилки при моделюванні об'єкта. Це, в свою чергу, в реальних умовах може викликати порушення роботи виробу або навіть поломки останнього. У зв'язку з цим були розроблені методи програмування в обмеженнях, що дозволяють машині знайти правильне рішення виникаючої проблеми. Підхід, запропонований у цій роботі, використовує методи інтервальної математики, що дозволяє по-новому поглянути на способи завдання обмежень.

2. Мета і задачі дослідження та заплановані результати

Метою дослідження є проектування і розробка програми, що реалізує моделювання заданого об'єкта за допомогою методу кінцевих елементів, модифікованого для програмування в обмеженнях.

Основні задачі дослідження:

  1. Аналіз методів розробки систем CAE.
  2. Реалізація методу програмування в обмеженнях.
  3. Обґрунтування вимог до створюваної системи, а також до вхідних параметрів, що вводяться користувачем.
  4. Опис алгоритму роботи програми.
  5. Оцінка ефективності застосування програмування в обмеженнях при роботі з різними моделями.

Об'єкт дослідження: реалізація модифікованої для дослідження програмування в обмеженнях системи CAE.

Предмет дослідження: ефективність застосування програмування в обмеженнях в рамках підсистеми CAE сучасних САПР.

3. Огляд досліджень та розробок

Питання використання в САПР програмування в обмеженнях і інтервальної математики було досліджено як вітчизняними, так і зарубіжними фахівцями. Цьому присвячений ряд робіт, в основному, вітчизняних дослідників.

3.1 Огляд міжнародних джерел

Christoph M. Hoffmann у своїй роботі «Constraint-Based CAD» розглядає поточний етап розвитку САПР і особливо виділяє наявні способи завдання обмежень при проектуванні виробів, їх переваги та недоліки. Також автор пропонує ідею САПР, заснованої на завданні обмежень.[1]

Nikhil Somani, Andre Gaschler, Markus Rickert, Alexander Perzylo і Alois Knol в своїй статті «Constraint-Based task Programming with CAD Semantics:From Intuitive Specifcation to Real-Time Control» описують можливість управління роботами за допомогою програмного комплексу САПР і взаємопов'язаних геометричних обмежень.[2]

3.2 Огляд національних джерел

У роботі «Об'єктно-орієнтоване програмування в обмеженнях: новий підхід на основі декларативних мов моделювання даних» Семенов В.А., Ільїн Д.В., Морозов С.В., Сидяка О.В. розглядають і обговорюють новий системний підхід до реалізації об'єктно-орієнтованого програмування в обмеженнях на основі використання декларативних мов моделювання даних.[3]

Наріньяні А.С. у своїй роботі «Введення в недоопределенність» знайомить читача з методом недоопределенних моделей, запропонованим автором в 80-х роках минулого століття для представлення і обробки не повністю визначених знань.[4]

3.3 Огляд локальних джерел

У Донецькому національному технічному університеті тема програмування в обмеженнях в рамках САПР поширена серед магістрів.

Р.Є. Комаричев у своїй магістерській роботі «Аналіз технологій програмної реалізації методу скінченних елементів» займався дослідженням розробки систем, що реалізують метод кінцевих елементів в різних моделях в САПР, будь то фізичний, термічний або аеродинамічний вплив на виріб з подальшим виведенням результатів моделювання. Також в роботі їм були виявлені кілька потенційних ділянок для оптимізації МКЕ.[5]

С.Д. Крилевич та О.В. Григор'єв у статті «Розробка системи автоматизованого рішення обчислювальних задач САПР, заснованої на методі програмування в обмеженнях» розглянули методи реалізації інструментальної системи для розв'язання задач програмування в обмеженнях у різних постановках, що виникають у процесі роботи проблемно-орієнтованих САПР. Були визначені постановки завдань розроблюваної системи програмування в обмеженнях, а також структури даних її моделі. Була розроблена загальна динамічна обчислювальна модель, здатна забезпечити вирішення поставлених завдань.[6]

4. Метод скінченних елементів як основа розрахунків при моделюванні

Одним з найбільш використовуваних методів моделювання в сучасних САПР є метод кінцевих елементів (МКЕ). Він представляє з себе чисельний метод вирішення диференціальних рівнянь з частковими похідними, а також інтегральних рівнянь, що виникають при вирішенні задач прикладної фізики. Метод широко використовується для вирішення задач механіки деформованого твердого тіла, теплообміну, гідродинаміки, електродинаміки та топологічної оптимізації.

Як уже згадувалося, зараз МКЕ є одним з найбільш популярних інструментів дослідження характеристик інженерних конструкцій, що піддаються різним навантаженням. Традиційні методи, які передбачають суворе теоретичне обгрунтування, можуть використовуватися тільки для обмеженого класу завдань і особливих умов навантаження. Вони часто потребують модифікації, причому доводиться контролювати їх застосовність до вирішення поставленого завдання. Невпевненість конструкторів в достовірності отриманих результатів змушує їх підвищувати граничні навантаження, що призводить до включення в конструкцію додаткових кріпильних секцій, перевитрати матеріалів і підвищення загальної вартості виробу.[7]

Суть методу кінцевих елементів укладена в його назві. Область, в якій шукається рішення диференціальних рівнянь, розбивається на кінцеву кількість підобластей, і в кожній з них довільно вибирається вид апроксимуючої функції. У найпростішому випадку це поліном першого ступеня. Поза своїм елементом апроксимуюча функція дорівнює нулю. Значення функцій на кордонах елементів (у вузлах) є вирішенням задачі і заздалегідь невідомі. Коефіцієнти апроксимуючих функцій зазвичай шукаються з умови рівності значення сусідніх функцій на кордонах між елементами, тобто у вузлах. Потім ці коефіцієнти виражаються через значення функцій у вузлах елементів. Складається система лінійних алгебраїчних рівнянь, в якій кількість рівнянь дорівнює кількості невідомих значень у вузлах, на яких шукається рішення вихідної системи, прямо пропорційно кількості елементів і обмежується тільки можливостями ЕОМ. Так як кожен з елементів пов'язаний з обмеженою кількістю сусідніх, система лінійних алгебраїчних рівнянь має розріджений вигляд, що істотно спрощує її рішення.[8]

Після розбивки на кінцеві елементи подальші розрахунки проводяться для окремих кінцевих елементів, кожен з них вносить свій вклад в характеристику міцності деталі. Точки, що обмежують елемент, називають вузлами, які разом з проходять через них лініями утворюють кінцеву елементну сітку.

Для двовимірних областей найбільш часто використовуються елементи у формі трикутника і чотирикутника. При цьому елементи можуть мати як прямокутні, так і криволінійні межі, що дозволяє з достатнім ступенем точності апроксимувати кордон будь-якої форми. Для тривимірних областей найбільш вживаними є елементи у формі тетраедра і паралелепіпеда, які також можуть мати прямо- і криволінійні межі.[7]

Очевидно, що для різних завдань використовуються різні моделі кінцевих елементів. Також використовуються різні типи елементів і координатні функції. У разі, якщо потрібно розглянути роботу більш детальної моделі, може бути збільшена щільність сітки кінцевих елементів за допомогою зменшення їх розміру.[9]

Довгий час широкому поширенню МКЕ заважало відсутність алгоритмів автоматичного розбиття області на «майже рівносторонні» трикутники (похибка, в залежності від варіації методу, обернено пропорційна синусу або найгострішого, або самого тупого кута в розбитті). Втім, це завдання вдалося успішно вирішити (алгоритми засновані на тріангуляції Делоне), що дало можливість створювати повністю автоматичні конечноелементні САПР.

Продемонструємо приклад роботи методу кінцевих елементів. Для цього використовуємо деякий циліндричний об'єкт і змоделюємо для нього пружну деформацію. Як можна помітити, об'єкт розбитий на безліч прямокутних елементів, в початковому стані забарвлених в синій колір, що вказує на нульову деформацію. Після початку моделювання деформації забарвлення деяких елементів змінюється - таким чином можна визначити, які частини виробу найбільш деформовані в даному експерименті.

Демонстрація завдання деформації

Рисунок 1 – Демонстрація завдання деформації
(анімація: 4 кадри, 608 кілобайт)

5. Використання програмування в обмеженнях в САПР

Для користувача САПР буває важко передбачити всі фактори, які будуть впливати на модельований об'єкт в реальному житті, а тому потрібно зменшувати точність моделювання. В такому випадку потрібно скористуватися методом програмування в обмеженнях.

Програмування в обмеженнях є за своєю суттю максимально декларативним і засноване на описі моделі задачі, а не алгоритму її вирішення. Модель специфицируется у вигляді невпорядкованої сукупності відносин, які відповідають зв'язкам, існуючим між параметрами завдання. Ці відносини, звані "обмеженнями", можуть мати вигляд рівнянь, нерівностей, логічних виразів і т. п.

У найзагальнішому вигляді постановка завдання в парадигмі програмування в обмеженнях формулюється наступним чином. Нехай на змінні x1, x2 ..., xn, областями значень яких є множини (X1 , X2 , ..., Xn), задані обмеження Ci (x1 , x2 , ..., xn), i = 1, k. потрібно знайти набори значень (A1, A2,..., an) (ai належить Xi), які б задовольняли всім обмеженням одночасно.[10]

Така постановка задачі називається проблемою задоволення обмежень, а для її вирішення використовуються різні алгоритми і методи. Зокрема, проблема задоволення обмежень може формулюватися як система рівнянь з числовими параметрами, а для її вирішення можуть використовуватися стандартні чисельні методи. Це досить підходяще рішення для вирішення задач моделювання, але не завжди ефективно для реальних умов, оскільки не всі типи даних можуть бути використані в таких задачах.

Одним з найбільш розвинених і практично значущих підходів, що відносяться до програмування в обмеженнях, є недовизначені моделі.

Технологія недовизначених моделей виділяється серед інших підходів обчислювальною потужністю, універсальністю і ефективністю. Фактично, вона є єдиною технологією, яка дозволяє вирішувати завдання задоволення обмежень в самій що ні на є загальній постановці.

В основі апарату недовизначених моделей лежать наступні поняття:

- Недовизначена змінна - деяка непуста підмножина, що містить всередині себе значення-денотат, що зважаючи на нестачу інформації залишається невідомим; доступна оцінка реального значення;

- Недовизначене розширення - будь-яка кінцева система підмножин множини Х, замкнута щодо операції перетину і містить весь універсум і порожню множину. Для одного і того ж універсуму можуть існувати кілька різних недовизначених розширень.[11]

Деякі властивості звичайних операцій істотно змінюються у відповідних недовизначених розширеннях. Як приклад розглянемо добре відому властивість адитивних операцій над числами (цілими або дійсними), що сума будь-якого числа і зворотного йому дорівнює єдиному нульовому елементу.

a + (-a) = 0

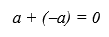
Нехай в якості недовизначеного розширення множини чисел буде інтервальне недовизначене розширення, а відповідні недовизначені розширення операцій мінус (*-) і плюс (*+) визначені згідно відомим правилам інтервальної арифметики. Таким чином, недовизначене розширення унарного мінуса має наступний вигляд:

[aLo, aUp] = [-aUp , -aLo]

Недовизначене розширення додавання (a = b *+ c) обчислюється подібним чином:

[aLo, aUp] = [bLo + cLo , bUp + cUp]

В такому випадку, недовизначене розширення виразу (a + (-a) = 0) має такий вигляд:

[aLo, aUp] *+ (*-[aLo, aUp]) = [aLo, aUp] *+ [-aUp, -aLo] = [aLo + (-aUp), aUp+ (-aLo)] = [aLo - aUp, aUp - aLo ]

Таким чином, якщо нижня і верхня межі недовизначеного числа не збігаються, інтервал [aLo - aUp , aUp - aLo] тільки містить в собі нульовий елемент, але не дорівнює йому.[11]

Роблячи висновок з вищесказаного, в недовизначених моделях досить важливо, в якому вигляді представлені умови завдання, що може стати істотним доповненням до методу кінцевих елементів.

Висновки

Підсумовуючи описані твердження, використання технології недоопределенних моделей дозволить використовувати в задачах задоволення обмежень не тільки дискретні, але і інтервальні значення змінних. Передбачається, що включення інтервальної математики в МКЕ може покращити його роботу в деяких модельованих ситуаціях.

При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: червень 2023 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після вказаної дати.

Перелік посилань

  1. Christoph M. Hoffmann. (2005). Constraint-Based Computer-Aided Design. Journal of Computing and Information Science in Engineering 5(3):182. DOI:10.1115/1.1979508 [Посилання]
  2. Nikhil Somani, Andre Gaschler, Markus Rickert, Alexander Perzylo, Alois Knol. (2015). Constraint-Based Task Programming with CAD Semantics: From Intuitive Specification to Real-Time Control. IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS)At: Hamburg, Germany. DOI:10.1109/IROS.2015.7353770 [Посилання]
  3. Семенов В.А., Ильин Д.В., Морозов С.В., Сидяка О.В. Объектно-ориентированное программирование в ограничениях: новый подход на основе декларативных языков моделирования данных [Электронный ресурс] // КиберЛенинка - научная электронная библиотека. - Режим доступа: [Посилання]
  4. Нариньяни А.С. Введение в недоопределенность [Электронный ресурс] // КиберЛенинка - научная электронная библиотека. - Режим доступа: [Посилання]
  5. Комаричев Р.Е. Анализ технологий программной реализации метода конечных элементов [Электронный ресурс] // Портал магистров ДонНТУ. — Режим доступа: [Посилання]
  6. Крилевич, С.Д., Григорьев, А.В. Разработка системы автоматизированного решения вычислительных задач САПР, основанной на методе программирования в ограничениях [Электронный ресурс] // Электронный архив Донецкого Национального Технического Университета (г. Донецк). - Режим доступа: [Посилання]
  7. Чернышов Д.Н., Грищенко О.С., Григорьев А.В. Использование метода конечных элементов для физических расчетов в САПР // Материалы VI Международной научно-технической конференции «Современные информационные технологии в образовании и научных исследованиях» (СИТОНИ-2019). – Донецк: ДонНТУ, 2019. - С. 347-352.
  8. Чернышов Д.Н., Григорьев А.В., Воробьев Л.О. Расширение функциональных возможностей подсистем моделирования и инжиниринга (CAE) в современных САПР. // Материалы студенческой секции X Международной научно-технической конференции «Информатика, управляющие системы, математическое и компьютерное моделирование» (ИУСМКМ -2021). –Донецк: ДОННТУ, 2021. - С. 100-104.
  9. Основные этапы решения задач методом конечных элементов - САПР конструктора машиностроителя [Электронный ресурс] // Студенческие реферативные статьи и материалы. - Режим доступа: [Посилання]
  10. Ушаков Д.М., Телерман В.В. Системы программирования в ограничениях (обзор) // Системная информатика: Сб. науч. тр. Новосибирск: Наука, 2000. Вып.7: Проблемы теории и методологии создания параллельных и распределенных систем. С. 275—310.
  11. Нариньяни А.С. Недоопределенные модели и операции с недоопределенными значениями. – Новосибирск, 1982. – 33с.