UA   EN
ДонНТУ   Портал магистров

Реферат по теме выпускной работы

Содержание

Введение

САПР, или системы автоматизированного проектирования – это цифровые платформы, созданные для повышения эффективности труда инженеров, поскольку в наше время мало кто предпочитает бумажные чертежи электронным. Они находят широкое применение практически во многих сферах производственной и строительной деятельности.

В наше время компьютерные технологии бурно развиваются, и комплексы САПР получают всё более качественные возможности для дизайна объектов и их моделирования в условиях физических и температурных нагрузок, а также расчёта аэро- и гидродинамики проектируемых моделей. Таким образом, улучшение точности моделирования является одной из главных задач модернизации САПР.

1. Актуальность темы

Комплексы САПР разбиты на подсистемы, и той, которая отвечает за моделирование объектов, является CAE - Computer-Aided Engineering. CAE представляет из себя комплекс программных продуктов, которые могут дать пользователю характеристику того, как в реальности будет вести себя разработанная на компьютере модель изделия. При помощи CAE инженер может достаточно точно оценить работоспособность изделия, не прибегая при этом к значительным временным и денежным затратам. В своей работе CAE используют различные математические расчёты: метод конечных элементов, метод конечных объемов, метод конечных разностей.

Зачастую бывает, что чрезмерная точность используемых математических расчётов может быть причиной ошибки при моделировании объекта. Это, в свою очередь, в реальных условиях может вызвать нарушение работы изделия или даже поломки последнего. В связи с этим были разработаны методы программирования в ограничениях, позволяющие машине найти правильное решение возникающей проблемы. Подход, предлагаемый в этой работе, использует методы интервальной математики, что позволяет по-новому взглянуть на способы задания ограничений.

2. Цель и задачи исследования, планируемые результаты

Целью работы является проектирование и разработка приложения, реализующего моделирование заданного объекта при помощи метода конечных элементов, модифицированного для программирования в ограничениях с использованием интервальной математики.

Основные задачи исследования:

  1. Анализ методов разработки систем CAE.
  2. Реализация метода программирования в ограничениях.
  3. Обоснование требований к создаваемой системе, а также к входным параметрам, вводимых пользователем.
  4. Описание алгоритма работы программы.
  5. Оценка эффективности применения программирования в ограничениях при работе с различными моделями.

Объект исследования: реализация модифицированной для исследования программирования в ограничениях системы CAE.

Предмет исследования: эффективность применения программирования в ограничениях в рамках подсистемы CAE современных САПР.

3. Обзор исследований и разработок

Вопрос использования в САПР программирования в ограничениях и интервальной математики был исследован как отечественными, так и зарубежными специалистами. Этому посвящен ряд работ, в основном, отечественных исследователей.

3.1 Обзор международных источников

Christoph M. Hoffmann в своей работе «Constraint-Based CAD» рассматривает текущий этап развития САПР и особо выделяет имеющиеся способы задания ограничений при проектировании изделий, их преимущества и недостатки. Также автор предлагает идею САПР, основанной на задании ограничений.[1]

Nikhil Somani, Andre Gaschler, Markus Rickert, Alexander Perzylo и Alois Knol в своей статье «Constraint-Based Task Programming with CAD Semantics:From Intuitive Specifcation to Real-Time Control» описывают возможность управления роботами с помощью программного комплекса САПР и взаимосвязанных геометрических ограничений.[2]

3.2 Обзор национальных источников

В работе «Объектно-ориентированное программирование в ограничениях: новый подход на основе декларативных языков моделирования данных» Семенов В.А., Ильин Д.В., Морозов С.В., Сидяка О.В. рассматривают и обсуждают новый системный подход к реализации объектно-ориентированного программирования в ограничениях на основе использования декларативных языков моделирования данных.[3]

Нариньяни А.С. в своей работе «Введение в недоопределённость» знакомит читателя с методом недоопределённых моделей, предложенным автором в 80-х годах прошлого столетия для представления и обработки не полностью определёных знаний.[4]

3.3 Обзор локальных источников

В Донецком национальном техническом университете тема программирования в ограничениях в рамках САПР распространена среди магистров.

Р.Е. Комаричев в своей магистерской работе «Анализ технологий программной реализации метода конечных элементов» занимался исследованием разработки систем, реализующих метод конечных элементов в различных моделях в САПР, будь то физическое, термическое или аэродинамическое воздействие на изделие с последующим выводом результатов моделирования. Также в работе им были выявлены несколько потенциальных участков для оптимизации МКЭ.[5]

С.Д. Крилевич и А.В. Григорьев в статье «Разработка системы автоматизированного решения вычислительных задач САПР, основанной на методе программирования в ограничениях» рассмотрели методы реализации инструментальной системы для решения задач программирования в ограничениях в различных постановках, возникающих в процессе работы проблемно-ориентированных САПР. Были определены постановки задач разрабатываемой системы программирования в ограничениях, а также структуры данных ее модели. Была разработана общая динамическая вычислительная модель, способная обеспечить решение поставленных задач.[6]

4. Метод конечных элементов как основа расчётов при моделировании

Одним из наиболее используемых методов моделирования в современных САПР является метод конечных элементов (МКЭ). Он представляет из себя численный метод решения дифференциальных уравнений с частными производными, а также интегральных уравнений, возникающих при решении задач прикладной физики. Метод широко используется для решения задач механики деформируемого твёрдого тела, теплообмена, гидродинамики, электродинамики и топологической оптимизации.

Как уже упоминалось, сейчас МКЭ является одним из наиболее популярных инструментов исследования характеристик инженерных конструкций, подвергаемых различным нагрузкам. Традиционные методы, предполагающие строгое теоретическое обоснование, могут использоваться только для ограниченного класса задач и особых условий нагрузки. Они часто нуждаются в модификации, причем приходится контролировать их применимость к решению поставленной задачи. Неуверенность конструкторов в достоверности полученных результатов заставляет их повышать предельные нагрузки, что приводит к включению в конструкцию дополнительных крепежных секций, перерасходу материалов и повышению общей стоимости изделия.[7]

Суть метода конечных элементов заключена в его названии. Область, в которой ищется решение дифференциальных уравнений, разбивается на конечное количество подобластей, и в каждой из них произвольно выбирается вид аппроксимирующей функции. В простейшем случае это полином первой степени. Вне своего элемента аппроксимирующая функция равна нулю. Значения функций на границах элементов (в узлах) являются решением задачи и заранее неизвестны. Коэффициенты аппроксимирующих функций обычно ищутся из условия равенства значения соседних функций на границах между элементами, т. е. в узлах. Затем эти коэффициенты выражаются через значения функций в узлах элементов. Составляется система линейных алгебраических уравнений, в которой количество уравнений равно количеству неизвестных значений в узлах, на которых ищется решение исходной системы, прямо пропорционально количеству элементов и ограничивается только возможностями ЭВМ. Так как каждый из элементов связан с ограниченным количеством соседних, система линейных алгебраических уравнений имеет разрежённый вид, что существенно упрощает её решение.[8]

После разбивки на конечные элементы дальнейшие расчеты проводятся для отдельных конечных элементов, каждый из них вносит свой вклад в характеристику прочности детали. Точки, ограничивающие элемент, называют узлами, которые вместе с проходящими через них линиями образуют конечную элементную сетку.

Для двумерных областей наиболее часто используются элементы в форме треугольника и четырехугольника. При этом элементы могут иметь как прямоугольные, так и криволинейные границы, что позволяет с достаточной степенью точности аппроксимировать границу любой формы. Для трехмерных областей наиболее употребимыми являются элементы в форме тетраэдра и параллелепипеда, которые также могут иметь прямо- и криволинейные границы.[7]

Очевидно, что для разных задач используются разные модели конечных элементов. Также используются разные типы элементов и координатные функции. В случае, если требуется рассмотреть работу более детальной модели, может быть увеличена плотность сетки конечных элементов посредством уменьшения размера последних.[9]

Долгое время широкому распространению МКЭ мешало отсутствие алгоритмов автоматического разбиения области на «почти равносторонние» треугольники (погрешность, в зависимости от вариации метода, обратно пропорциональна синусу или самого острого, или самого тупого угла в разбиении). Впрочем, эту задачу удалось успешно решить (алгоритмы основаны на триангуляции Делоне), что дало возможность создавать полностью автоматические конечноэлементные САПР.

Продемонстрируем пример работы метода конечных элементов. Для этого используем некоторый цилиндрический объект и смоделируем для него упругую деформацию. Как можно заметить, объект разбит на множество прямоугольных элементов, в исходном состоянии окрашенных в синий цвет, что указывает на нулевую деформацию. После начала моделирования деформации окраска некоторых элементов меняется - таким образом можно определить, какие части изделия наиболее деформированы в данном эксперименте.

Демонстрация задачи деформации

Рисунок 1 – Демонстрация задачи деформации
(анимация: 4 кадра, 608 килобайт)

5. Использование программирования в ограничениях в САПР

Для пользователя САПР бывает трудно предвидеть все факторы, которые будут влиять на моделируемый объект в реальной жизни, а потому требуется уменьшать точность моделирования. В таком случае требуется воспользоваться методом программирования в ограничениях.

Программирование в ограничениях является по своей сути максимально декларативным и основано на описании модели задачи, а не алгоритма ее решения. Модель специфицируется в виде неупорядоченной совокупности отношений, которые соответствуют связям, существующим между параметрами задачи. Эти отношения, называемые «ограничениями», могут иметь вид уравнений, неравенств, логических выражений и т. п.

В самом общем виде постановка задачи в парадигме программирования в ограничениях формулируется следующим образом. Пусть на переменные x1, x2 ..., xn , областями значений которых являются множества (X1 , X2 , ..., Xn), заданы ограничения Ci (x1 , x2 , ..., xn), i=1, k. Требуется найти наборы значений (a1 , a2 , ..., an) (ai принадлежит Xi), которые бы удовлетворяли всем ограничениям одновременно.[10]

Такая постановка задачи называется проблемой удовлетворения ограничений, а для ее решения используются различные алгоритмы и методы. В частности, проблема удовлетворения ограничений может формулироваться как система уравнений с числовыми параметрами, а для ее решения могут использоваться стандартные численные методы. Это достаточно подходящее решение для решения задач моделирования, но не всегда эффективно для реальных условий, поскольку не все типы данных могут быть использованы в таких задачах.

Одним из наиболее развитых и практически значимых подходов, относящихся к программированию в ограничениях, являются недоопределённые модели.

Технология недоопределённых моделей выделяется среди других подходов вычислительной мощностью, универсальностью и эффективностью. Фактически, она является единственной технологией, которая позволяет решать задачу удовлетворения ограничений в самой что ни на есть общей постановке.

В основе аппарата недоопределённых моделей лежат следующие понятия:

- Недоопределённая переменная – некоторое непустое подмножество, содержащее внутри себя значение-денотат, ввиду недостатка информации остающееся неизвестным; доступная оценка реального значения;

- Недоопределённое расширение – любая конечная система подмножеств множества Х, замкнутая относительно операции пересечения и содержащая весь универсум и пустое множество. Для одного и того же универсума могут существовать несколько различных недоопределённых расширений.[11]

Некоторые свойства обычных операций существенно меняются в соответствующих недоопределённых расширениях. Как пример рассмотрим хорошо известное свойство аддитивных операций над числами (целыми или вещественными), что сумма любого числа и обратного ему равна единственному нулевому элементу.

a + (-a) = 0

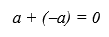
Пусть в качестве недоопределённого расширения множества чисел будет интервальное недоопределённое расширение, а соответствующие недоопределённые расширения операций минус (*-) и плюс (*+) определены согласно известным правилам интервальной арифметики. Таким образом, недоопределённое расширение унарного минуса имеет следующий вид:

[aLo, aUp] = [-aUp , -aLo]

Недоопределённое расширение сложения (a = b *+ c) вычисляется подобным образом:

[aLo, aUp] = [bLo + cLo , bUp + cUp]

В таком случае, недоопределённое расширение выражения (a + (-a) = 0) имеет следующий вид:

[aLo, aUp] *+ (*-[aLo, aUp]) = [aLo, aUp] *+ [-aUp, -aLo] = [aLo + (-aUp), aUp+ (-aLo)] = [aLo - aUp, aUp - aLo ]

Таким образом, если нижняя и верхняя границы недоопределённого числа не совпадают, интервал [aLo - aUp , aUp - aLo] всего лишь содержит в себе нулевой элемент, но не равен ему в точности.[11]

Делая вывод из вышесказанного, в недоопределённых моделях весьма существенно, в каком виде представлены условия задачи, что может стать важным дополнением к методу конечных элементов.

Выводы

Суммируя описанные утверждения, использование технологии недоопределённых моделей позволит использовать в задачах удовлетворения ограничений не только дискретные, но и интервальные значения переменных. Предполагается, что включение интервальной математики в МКЭ может улучшить его работу в некоторых моделируемых ситуациях.

При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: июнь 2023 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.

Список источников

  1. Christoph M. Hoffmann. (2005). Constraint-Based Computer-Aided Design. Journal of Computing and Information Science in Engineering 5(3):182. DOI:10.1115/1.1979508 [Ссылка]
  2. Nikhil Somani, Andre Gaschler, Markus Rickert, Alexander Perzylo, Alois Knol. (2015). Constraint-Based Task Programming with CAD Semantics: From Intuitive Specification to Real-Time Control. IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS)At: Hamburg, Germany. DOI:10.1109/IROS.2015.7353770 [Ссылка]
  3. Семенов В.А., Ильин Д.В., Морозов С.В., Сидяка О.В. Объектно-ориентированное программирование в ограничениях: новый подход на основе декларативных языков моделирования данных [Электронный ресурс] // КиберЛенинка - научная электронная библиотека. - Режим доступа: [Ссылка]
  4. Нариньяни А.С. Введение в недоопределенность [Электронный ресурс] // КиберЛенинка - научная электронная библиотека. - Режим доступа: [Ссылка]
  5. Комаричев Р.Е. Анализ технологий программной реализации метода конечных элементов [Электронный ресурс] // Портал магистров ДонНТУ. — Режим доступа: [Ссылка]
  6. Крилевич, С.Д., Григорьев, А.В. Разработка системы автоматизированного решения вычислительных задач САПР, основанной на методе программирования в ограничениях [Электронный ресурс] // Электронный архив Донецкого Национального Технического Университета (г. Донецк). - Режим доступа: [Ссылка]
  7. Чернышов Д.Н., Грищенко О.С., Григорьев А.В. Использование метода конечных элементов для физических расчетов в САПР // Материалы VI Международной научно-технической конференции «Современные информационные технологии в образовании и научных исследованиях» (СИТОНИ-2019). – Донецк: ДонНТУ, 2019. - С. 347-352.
  8. Чернышов Д.Н., Григорьев А.В., Воробьев Л.О. Расширение функциональных возможностей подсистем моделирования и инжиниринга (CAE) в современных САПР. // Материалы студенческой секции X Международной научно-технической конференции «Информатика, управляющие системы, математическое и компьютерное моделирование» (ИУСМКМ -2021). –Донецк: ДОННТУ, 2021. - С. 100-104.
  9. Основные этапы решения задач методом конечных элементов - САПР конструктора машиностроителя [Электронный ресурс] // Студенческие реферативные статьи и материалы. - Режим доступа: [Ссылка]
  10. Ушаков Д.М., Телерман В.В. Системы программирования в ограничениях (обзор) // Системная информатика: Сб. науч. тр. Новосибирск: Наука, 2000. Вып.7: Проблемы теории и методологии создания параллельных и распределенных систем. С. 275—310.
  11. Нариньяни А.С. Недоопределенные модели и операции с недоопределенными значениями. – Новосибирск, 1982. – 33с.