Реферат по теме выпускной работы
Содержание
- Введение
- 1. Постановка задачи реферата
- 2. Понятие и свойства кластеризации
- 3. Классификация и обзор алгоритмов
- 3.1 Алгоритмы иерархической кластеризации
- 3.2 Алгоритмы квадратичной ошибки
- 3.3 Нечёткие алгоритмы
- 3.4 Алгоритмы, основанные на теории графов
- 3.5 Алгоритмы выделения связных компонент
- 3.6 Алгоритм минимального покрывающего дерева
- 4. Сравнительное вычисление сложности алгоритмов
- Выводы
- Список источников
Введение
При анализе и прогнозировании социально-экономических явлений исследователи часто сталкиваются с многомерным характером их описаний. Это происходит при решении задачи сегментации рынка, построении типологии страны на основе достаточного количества показателей, прогнозировании рыночной ситуации отдельных товаров, изучении и прогнозировании экономической депрессии и многих других проблемах [1].
Многомерный аналитический метод является наиболее эффективным количественным инструментом для изучения социально-экономических процессов, описываемых большим количеством характеристик. Сюда входят кластерный анализ, таксономия, распознавание образов и факторный анализ.
Кластерный анализ наиболее четко отражает характеристики классификации при изучении коммуникаций, многомерный анализ – при факторном анализе [2].
Подход к кластерному анализу иногда упоминается в литературе как числовая классификация, numerical classification, самообучающееся распознавание и т.д.
Первое применение кластерному анализу было найдено в социологии. Название cluster analysis происходит от английского слова cluster -скопление, кластерная группа. Впервые в 1939 году был определен предмет кластерного анализа, описание которого было проведено исследователем Трайоном. Основная цель кластерного анализа – разделить множество изучаемых объектов и признаков на однородные группы или кластеры в соответствующем смысле. Это означает, что задача классификации данных и выявления в них соответствующей структуры решена. Метод кластерного анализа может быть использован в самых разных случаях, будь то простая группировка или все сводится к формированию групп на основе количественного сходства.
Большое преимущество кластерного анализа в том, что вы можете разделить объект по целому набору функций, а не по одному параметру. Кроме того, кластерный анализ, в отличие от большинства математических и статистических методов, не накладывает ограничений на тип рассматриваемого объекта, позволяя рассматривать различные исходные данные практически любого характера. Это, например, очень важно для прогнозирования рыночных условий, когда показатели имеют различный внешний вид и затрудняют применение традиционных эконометрических подходов.
Кластерный анализ может учитывать довольно большой объем информации и значительно сокращать, сжимать и делать большие объемы социально-экономической информации компактными и наглядными [3].
Кластерный анализ имеет большое значение в отношении набора временных рядов, характеризующих экономическое развитие (например, сочетание экономики и товаров в целом). Здесь вы можете выделить периоды, в которых значения соответствующих показателей были очень близки, или группы временных рядов с наиболее схожей динамикой.
Вы можете периодически использовать кластерный анализ. В этом случае исследование проводится до тех пор, пока не будут достигнуты необходимые результаты. В тоже время каждый цикл здесь может предоставить информацию, которая может существенно изменить направление и подход к дальнейшему применению кластерного анализа. Этот процесс может быть представлен системой обратной связи.
В задаче социально-экономического прогнозирования сочетание кластерного анализа с другими количественными методами (например, регрессионным анализом) является очень перспективным.
1. Постановка задачи реферата
В данном реферате будут описаны и разобраны понятие кластеризации, изучить меры расстояний, классификацию алгоритмов кластеризации и сравнить вычислительную сложность алгоритмов.
Цель реферата – описание понятия кластеризация, обзор и сравнение существующих алгоритмов кластеризации.
В данном реферате будут рассмотрены:
- понятие кластеризации;
- свойства кластеризации;
- классификация алгоритмов кластеризации;
- сравнение вычислительной сложности алгоритмов кластеризации.
2. Понятие и свойства кластеризации
Кластерный анализ, также известный как кластеризация, представляет собой метод интеллектуального анализа данных, предназначенный для группировки похожих точек в кластеры. Основная цель такого анализа – разбиение набора данных на группы таким образом, чтобы точки данных внутри одного кластера были более схожи друг с другом, чем с точками данных из других кластеров [4].
Этот метод широко применяется в исследовательском анализе данных и позволяет выявить скрытые закономерности и взаимосвязи. Существует множество алгоритмов кластерного анализа, таких как k-средних, иерархическая кластеризация и кластеризация на основе плотности. Выбор конкретного алгоритма зависит от специфики поставленной задачи и характеристик анализируемых данных.
По сути, кластерный анализ – это процесс выявления схожих групп объектов для их объединения в кластеры. Он относится к алгоритмам машинного обучения без учителя и работает с немаркированными данными. Каждый кластер представляет собой группу точек, в которой все объекты принадлежат к одной категории.
Кластеризация (или кластерный анализ) представляет собой процесс группировки объектов на основе их сходства. Этот метод находит применение в различных областях, таких как машинное обучение, компьютерная графика, распознавание образов, анализ изображений, информационный поиск, биоинформатика и сжатие данных.
Концепция кластеров является достаточно сложной, что объясняет наличие множества различных алгоритмов для их определения. Существуют различные модели кластеров, и для каждой из них могут применяться свои алгоритмы. Кластеры, полученные с помощью одного алгоритма, будут отличаться от кластеров, выявленных другим методом.
В контексте машинного обучения мы часто начинаем с группировки примеров, чтобы лучше понять набор данных. Процесс группировки немаркированных примеров называется кластеризацией. Поскольку образцы не имеют меток, кластеризация относится к методам машинного обучения без контроля. Если же примеры имеют метки, то это уже классификация.
Свойства кластеризации [5]:
- Масштабируемость: в условиях огромного объёма данных, с которыми приходится работать, алгоритмы кластеризации должны быть способны масштабироваться. Это необходимо для эффективной обработки больших баз данных. Если данные не масштабируемы, результаты могут оказаться недостоверными.
- Высокая размерность: алгоритм должен быть способен обрабатывать данные в пространствах с высокой размерностью, а также работать с небольшими наборами данных.
- Универсальность: алгоритмы кластеризации должны поддерживать работу с различными типами данных. Это включает в себя возможность обработки дискретных, категориальных, интервальных и двоичных данных, а также других форматов.
- Работа с неструктурированными данными: в некоторых базах данных могут встречаться пропущенные значения, а также шумные или ошибочные данные. Если алгоритмы чувствительны к таким аномалиям, это может привести к образованию некачественных кластеров. Поэтому они должны быть способны обрабатывать неструктурированные данные и придавать им определённую структуру, группируя их по схожести. Это облегчает задачу специалиста по обработке данных и способствует выявлению новых закономерностей.
- Интерпретируемость: результаты кластеризации должны быть понятными, доступными для анализа и практического применения. Интерпретируемость показывает, насколько легко можно осмыслить данные.
3. Классификация и обзор алгоритмов
Были выделены две основные классификации алгоритмов кластеризации [6].
1. Иерархические и плоские.
Иерархические алгоритмы (также называемые алгоритмами таксономии) строят не одно разбиение выборки на непересекающиеся кластеры, а систему вложенных разбиений. Таким образом на выходе мы получаем дерево кластеров, корнем которого является вся выборка, а листьями – наиболее мелкие кластера. Плоские алгоритмы строят одно разбиение объектов на кластеры.
2. Четкие и нечеткие.
Четкие (или непересекающиеся) алгоритмы каждому объекту выборки ставят в соответствие номер кластера, т.е. каждый объект принадлежит только одному кластеру. Нечеткие (или пересекающиеся) алгоритмы каждому объекту ставят в соответствие набор вещественных значений, показывающих степень отношения объекта к кластерам. Т.е. каждый объект относится к каждому кластеру с некоторой вероятностью.
3.1 Алгоритмы иерархической кластеризации
Среди алгоритмов иерархической кластеризации выделяются два основных типа: восходящие и нисходящие алгоритмы. Нисходящие алгоритмы работают по принципу «сверху-вниз»: в начале все объекты помещаются в один кластер, который затем разбивается на все более мелкие кластеры [7]:
Для вычисления расстояний между кластерами чаще все пользуются двумя расстояниями: одиночной связью или полной связью.
К недостатку иерархических алгоритмов можно отнести систему полных разбиений, которая может являться излишней в контексте решаемой задачи.
3.2 Алгоритмы квадратичной ошибки
Задачу кластеризации можно рассматривать как построение оптимального разбиения объектов на группы. При этом оптимальность может быть определена как требование минимизации среднеквадратической ошибки разбиения, согласно формуле (1):
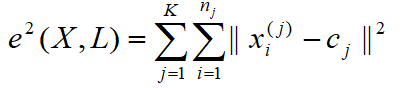
где cj – «центр масс» кластера j (точка со средними значениями характеристик для данного кластера).
К недостаткам данного алгоритма можно отнести необходимость задавать количество кластеров для разбиения.
3.3 Нечёткие алгоритмы
Наиболее популярным алгоритмом нечеткой кластеризации является алгоритм c-средних (c-means). Он представляет собой модификацию метода k-средних. Шаги работы алгоритма [8]:
1.Выбрать начальное нечеткое разбиение n объектов на k кластеров путем выбора матрицы принадлежности U размера n x k.
2.Используя матрицу U, найти значение критерия нечеткой ошибки согласно формуле (2):
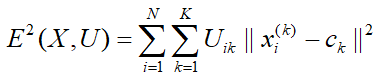
где ck – «центр масс» нечеткого кластера k, согласно формуле (3):
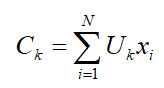
3.Перегруппировать объекты с целью уменьшения этого значения критерия нечеткой ошибки.
4.Возвращаться в п. 2 до тех пор, пока изменения матрицы U не станут незначительными.
Этот алгоритм может не подойти, если заранее неизвестно число кластеров, либо необходимо однозначно отнести каждый объект к одному кластеру.
3.4 Нечёткие алгоритмы
Суть таких алгоритмов заключается в том, что выборка объектов представляется в виде графа G= (V, E), вершинам которого соответствуют объекты, а ребра имеют вес, равный «расстоянию» между объектами. Достоинством графовых алгоритмов кластеризации являются наглядность, относительная простота реализации и возможность внесения различных усовершенствований, основанные на геометрических соображениях. Основными алгоритмам являются алгоритм выделения связных компонент, алгоритм построения минимального покрывающего (остовного) дерева и алгоритм послойной кластеризации [9]:
3.5 Алгоритмы выделения связных компонент
В алгоритме выделения связных компонент задается входной параметр R и в графе удаляются все ребра, для которых «расстояния» больше R. Соединенными остаются только наиболее близкие пары объектов. Смысл алгоритма заключается в том, чтобы подобрать такое значение R, лежащее в диапазон всех «расстояний», при котором граф «развалится» на несколько связных компонент. Полученные компоненты и есть кластеры [10]:
Для подбора параметра R обычно строится гистограмма распределений попарных расстояний. В задачах с хорошо выраженной кластерной структурой данных на гистограмме будет два пика – один соответствует внутрикластерным расстояниям, второй – межкластерным расстояния.
3.6 Алгоритм минимального покрывающего дерева
Алгоритм минимального покрывающего дерева сначала строит на графе минимальное покрывающее дерево, а затем последовательно удаляет ребра с наибольшим весом[11]. На рисунке 3.1 изображено минимальное покрывающее дерево, полученное для девяти объектов.
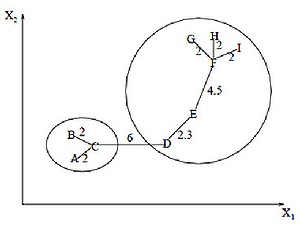
Рисунок 3.1 – Покрывающее дерево
Путём удаления связи, помеченной CD, с длиной равной 6 единицам (ребро с максимальным расстоянием), получаем два кластера: {A, B, C} и {D, E, F, G, H, I}. Второй кластер в дальнейшем может быть разделён ещё на два кластера путём удаления ребра EF, которое имеет длину, равную 4,5 единицам.
4. Сравнительное вычисление сложности алгоритмов
Вычислительная сложность алгоритмов приведена в таблице 4.1.
Таблица 4.1 – Вычислительная сложность алгоритмов
| Алгоритм кластеризации | Вычислительная сложность |
| Иерархический | O(n^2) |
| k-средних | O(nkl), где k – число кластеров, l – число итераций |
| c-средних | O(nkl), где k – число кластеров, l – число итераций |
| Выделение связных компонент | зависит от алгоритма |
| Минимальное покрывающее дерево | O(n^2 log(n)) |
Выводы
В реферате была представлена кластеризация, как уникальный метод, который позволяет разбить объекты на группы, не имея заранее заданной обучающей выборки или знания о природе этих классов. Модель самостоятельно определяет схожесть некоторых предметов и объединяет их в один сектор. Одним из преимуществ кластеризации является то, что она не требует знания о том, какие классы будут сформированы и сколько их будет. Научным названием кластеризации является unsupervised classification – из-за сходства постановки задачи.
Преимущества кластерного анализа:
- это может помочь выявить закономерности и взаимосвязи в наборе данных, которые могут быть неочевидны на первый взгляд;
- его можно использовать для исследовательского анализа данных, и он может помочь в выборе признаков;
- это может быть использовано для уменьшения размерности данных;
- его можно использовать для обнаружения аномалий и идентификации выбросов;
- его можно использовать для сегментации рынка и профилирования клиентов.
Недостатки кластерного анализа:
- он может быть чувствителен к выбору начальных условий и количеству кластеров;
- он может быть чувствителен к наличию шума или выбросов в данных;
- если кластеры плохо определены, может быть сложно интерпретировать результаты анализа;
- на результаты анализа может повлиять выбор используемого алгоритма кластеризации;
- важно отметить, что успех кластерного анализа зависит от данных, целей анализа и способности аналитика интерпретировать результаты.
Список источников
- Воронцов К.В. Алгоритмы кластеризации и многомерного шкалирования. / К.В. Воронцов - Курс лекций МГУ, 2021. – 520 с.
- Jain A. Data Clustering: A Review. / A. Jain, M. Murty, P. Flynn – ACM Computing Surveys, 2021. – 135 с.
- Котов А. Кластеризация данных. / А. Котов, Н. Красильников – М.: Феникс, 2019. – 358 с.
- Мандель И. Д. Кластерный анализ. – М.: Финансы и Статистика, 2022. – 242 с.
- Айвазян С.А. Прикладная статистика: классификация и снижение размерности. / С.А. Айвазян, В.М. Бухштабер, И.С. Енюков, Л.Д. Мешалкин – М.: Финансы и статистика, 2020. – 269 с.
- Круглов В.В. Искусственные нейронные сети. Теория и практика. / В.В. Круглов, В.В. Борисов – М.: Горячая линия – Телеком, 2021. - 311 с.
- Каллан Р. Основные концепции нейронных сетей. / Р. Каллан – М.:Вильямс, 2021. – 269 c.
- Воронцов К.В. Алгоритмы кластеризации и многомерного шкалирования. Курс лекций. МГУ, 2017. - 220 с.
- Руденко О.Г. Искусственные нейронные сети. / О.Г. Руденко, Е.В. Бодянский – Харьков: Феникс, 2019. - 302 с.
- Медведев В.С. Нейронные сети. MATLAB 6. / В.С. Медведев, В.Г. Потемкин – М.: ДИАЛОГ-МИФИ, 2022. - 314 с.
- Осовский С. Нейронные сети для обработки информации / С. Осовский; пер. с польского И. Рудинский – М.: Финансы и статистика, 2022. – 344 с.
