УСТОЙЧИВОСТЬ И ОЦЕНКА ПОГРЕШНОСТИ ПАРАЛЛЕЛЬНЫХ ОДНОШАГОВЫХ ЧИСЛЕННЫХ МЕТОДОВ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Введение
- Принципы построения параллельных вычислительных систем
- Пути достижения параллелизма
- Средства распараллеливания
- Классификация вычислительных систем
- Устойчивость решения задачи Коши для ОДУ
- Устойчивость разностных методов
- Устойчивость для жестких систем
- Устойчивость одношагового двухточечного метода
Выводы
Литература
ВВЕДЕНИЕ
К числу наиболее важных и перспективных направлений развития вычислительной техники, без сомнения, относится применение параллельных вычислительных систем. Для решения задач современной науки и техники возможностей существующих средств вычислительной техники оказывается недостаточно, а принципиальная ограниченность максимально возможного быстродействия обычных последовательных ЭВМ стала очевидной уже давно.
Существует широкий круг научно-технических задач, решение которых невозможно без использования высокопроизводительных вычислительных систем. К таким задачам можно отнести, в первую очередь, решение систем ОДУ. Задачи выдвигают специфические требования к продуктивности обработки информации, поэтому возникает необходимость в эффективной структурированной и алгоритммической организации параллельных вычислений. При адаптации численных методов решения систем ОДУ в вычислительных системах с параллельной архитектурой очень важным является вопрос устойчивости алгоритмов.
Дополнительные трудности обеспечения устойчивости появляются при численном решении жестких систем. Они
связаны с тем, что необходимо использовать специальные численные методы, позволяющие выбирать шаг интегрирования, исходя лишь из требований точности, а не устойчивости или из-за требования скорости итерационнного процесса решения неявных уравнений.
Основные результаты по теории устойчивости многошаговых методов были получены Дальквистом. Для интегрирования жестких систем широко используются неявные методы, предложенные и обоснованные Гиром. К настоящему времени предложен и пратически используется целый ряд методов, использующих последовательные алгоритмы решения жестких уравнений.
В то же время проблема разработки и обоснования параллельных методов и алгоритмов, ориентированных на эффективное использование в многопроцессорных системах, все еще остается открытой.
1. ПРИНЦИПЫ ПОСТРОЕНИЯ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ
1.1 Пути достижения параллелизма
Различают два способа параллельной обработки [1]: собственно параллельную и конвейерную.
Обобщенно говоря, под параллельными вычислениями понимаются процессы обработки данных, в которых происходит одновременное выполнение нескольких машинных операций. Для достижения параллелизма обязательно выполнение следующих требований к архитектурным принципам построения вычислительной системы:
- независимость функционирования отдельных устройств ЭВМ – данное требование относится в равной степени ко всем основным компонентам вычислительной системы – к устройствам ввода-вывода, к обрабатывающим процессорам и к устройствам памяти;
- избыточность элементов вычислительной системы – организация избыточности может осуществляться в следующих основных формах:
-
использование специализированных устройств таких, например, как отдельных процессоров для целочисленной и вещественной арифметики, устройств многоуровневой памяти (регистры, кэш);
- дублирование устройств ЭВМ путем использования, например, нескольких однотипных обрабатывающих процессоров или нескольких устройств оперативной памяти.
Подобный подход позволяет выполнять необходимые вычисления с меньшими затратами времени, и возможность получения максимального ускорения ограничивается только числом имеющихся процессоров и количеством "независимых" частей выполняемых вычислениях.
Идея конвейерной обработки данных состоит в разделении операции на отдельные этапы – ступени конвейера. Каждая ступень, выполнив свою работу, передает результат следующей ступени и одновременно принимает новую порцию входных данных. В результате, при вычислениях на таких устройствах могут находиться на разных стадиях обработки одновременно несколько различных элементов данных.
Современные многопроцессорные вычислительные системы (МВС) или суперкомпьютеры можно условно разделить на следующие классы [6]:
-
Векторно-конвейерные компьютеры, характеризующиеся наличием функциональных конвейерных устройств и набором векторных команд.
- Массивно-параллельные компьютеры с распределенной памятью, представляющие собой соединение микропроцессоров с помощью сетевого оборудования.
- Параллельные компьютеры с общей памятью, вся оперативная память которых разделяется несколькими одинаковыми процессорами, обращающимися к общей дисковой памяти. При этом проблем с обменом данными между процессорами и синхронизацией их работы, практически, не возникает. Вместе с тем главным недостатком такой архитектуры является то, что по чисто техническим причинам число процессоров, имеющих доступ к общей памяти, нельзя сделать большим.
- Кластерные компьютеры – класс суперкомпьютеров, представляющих собой комбинации предыдущих трех.
На сегодняшний день наиболее широкое распространение получили массивно-параллельные масштабируемые системы и кластеры серии МВС.
Суперкомпьютерная установка системы МВС представляет собой мультипроцессорный массив, объединенный с внешней дисковой памятью и устройствами ввода-вывода информации под общим управлением персонального компьютера или рабочей станции [2].
1.2 Средства распараллеливания
Существует два основных способа взаимодействия функциональных модулей МВС:
-
посредством разделения памяти (оперативной или внешней);
- посредством передачи сообщений.
Технология, реализующая первый способ взаимодействия между параллельными процессами, в основном, реализована в языках высокого уровня с внедренными в них функциями управления параллельной обработки данных. Для реализации второго способа распараллеливания пригодны, например, технологии MPI и DVM [3].
Предпочтительность использования той или иной технологии определяется следующими факторами:
- легкость программирования;
- эффективность разработанных программ;
- переносимость и повторное использование программ;
- качество средств отладки программ.
С этих позиций было проведено сравнение выше перечисленных технологий [3]. Приведем основные результаты этого исследования.
MPI ("Message passing interface" – "Взаимодействие через передачу сообщений") – одна из популярных технологий управления процессами в приложениях. Ее цели:
- создать интерфейс прикладного программирования;
- обеспечить возможность эффективных коммуникаций (избежать копирования из памяти в память, позволить совмещение вычислений и коммуникаций или разгрузку на коммуникационный процессор там, где он есть);
- определить интерфейс, который мог бы быстро быть реализован на многих продаваемых платформах без серьезной переделки ниже лежащего коммуникационного и системного ПО;
MPI предоставляет программисту единый механизм взаимодействия ветвей внутри параллельного приложения независимо от машинной архитектуры и взаимного расположения ветвей.
1.3 Классификация вычислительных систем
Существуют огромное количество способов классификации вычислительных систем. Среди них одним из наиболее распространенных является систематика Флинна, которая основывается на анализе способов взаимодействия последовательностей (потоков) выполняемых команд и обрабатываемых данных. В результате такого подхода различают следующие основные типы систем [4]:
- SISD (Single Instruction, Single Data) – системы, в которых существует одиночный поток команд и одиночный поток данных; к данному типу систем можно отнести обычные последовательные ЭВМ;
- SIMD (Single Instruction, Multiple Data) – системы с одиночным потоком команд и множественным потоком данных; подобный класс систем составляют МВС, в которых в каждый момент времени может выполняться одна и та же команда для обработки нескольких информационных элементов;
- MISD (Multiple Instruction, Single Data) – системы, в которых существует множественный поток команд и одиночный поток данных; примеров конкретных ЭВМ, соответствующих данному типу вычислительных систем, не существует; введение подобного класса предпринимается для полноты системы классификации;
- MIMD (Multiple Instruction, Multiple Data) – системы с множественным потоком команд и множественным потоком данных; к подобному классу систем относится большинство параллельных многопроцессорных вычислительных систем.
2. УСТОЙЧИВОСТЬ РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДУ
2.1 Устойчивость разностных методов
Пусть для численного решения задачи Коши
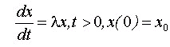
используется линейный m-шаговый разностный метод
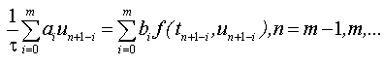
Pассмотрим также однородное разностное уравнение

и будем искать его решение, имеющие вид
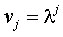
Откуда получим характеристическое уравнение разностного метода:
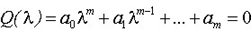
Разностный метод устойчив в смысле Дальквиста, если все корни характеристического уравнения
лежат внутри или на границе единичного круга комплексной плоскости, причем на границе единичного
круга нет кратных корней.
2.2 Устойчивость для жестких систем
При исследовании разностных методов для жестких систем уравнений обычно рассматривают уравнение вида
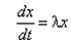
Характеристическое уравнение для данного модельного уравнения выглядит следующим образом:
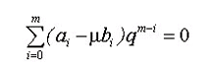
При численном решении жесткой задачи могут возникнуть некоторые трудности. Для того, чтобы обеспечить устойчивость
численного решения системы ОДУ, необходимо использовать такой шаг, при котором каждое из комплексных значений
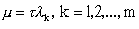
лежали бы внутри области устойчивости метода. При ограниченной
области устойчивости значение шага может оказаться столь малым, что провести численное решение на значительном интервале
времени интегрирования окажется практически невозможным. Чтобы устранить ограничение длины шага, обусловленное требованием
устойчивости были разработаны специальные численные методы.
Разностный метод
является А-устойчивым, если область его устойчивости содержит левую полуплоскость значений
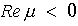
Для различных численных одношаговых методов решения задачи Коши для ОДУ был проведен анализ на устойчивость. Для примера ниже
приведено построение областей устойчивости метода Рунге-Кутта четвертого порядка точности.
Получено, что граница области устойчивости определяется следующим уравнением:
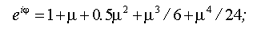
Построение этой кривой можно выполнить с помощью следующей программы в пакете Mathematica:
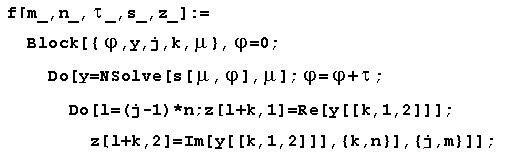
Обращаясь к которой получим границу и область устойчивости явного метода Рунге-Кутта четвертого порядка:

В результате выполнения данной программы были получены следующие результаты (рис. 2.1).
ниже.
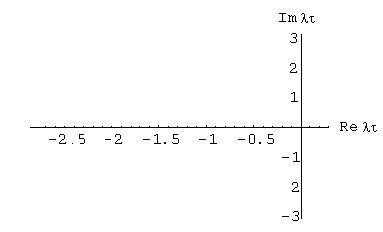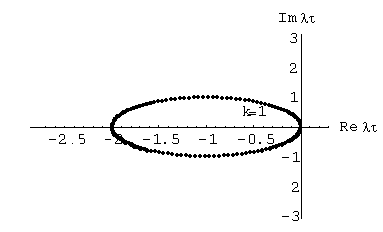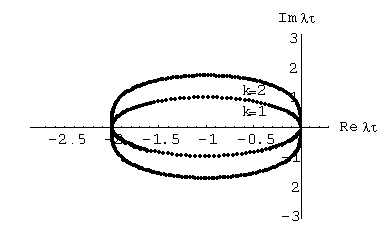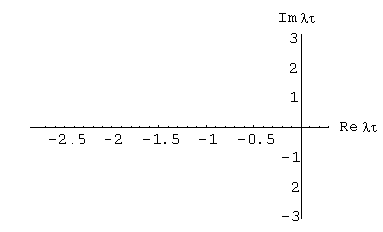
Рисунок 2.1 – Годографы устойчивости явных методов Рунге-Кутта разных порядков.
Из рис. 2.1 видно уникальное качество методов Рунге-Кутта: с ростом их порядка область устойчивости метода расширяется.
2.3 Устойчивость одношагового двухточечного метода
Исследование устойчивости блочных разностных схем при решении задачи Коши для систем обыкновенных дифференциальных уравнений
было проведено на модельном уравнении по схеме, примерно описанной выше.
В результате исследования были получены графики границ устойчивости (рис. 2.2).
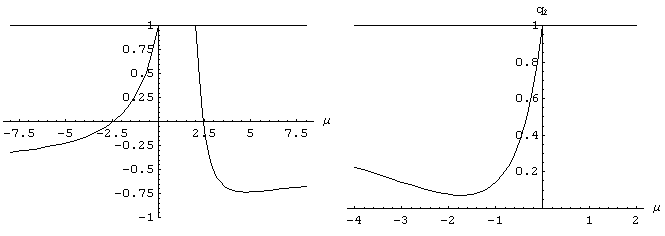
Рисунок 2.2 – Области устойчивости уравнений одношагового двухточечного метода.
С помощью средств системы Mathematica была получена граница устойчивости 1-го уравнения одношагового двухточечного метода (рис.2.3).
Областью устойчивости второго уравнения метода является левая полуплоскость.
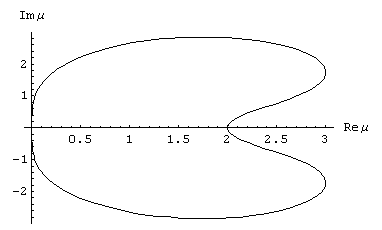
Рисунок 2.3 – Граница устойчивости 1-го уравнения одношагового двухточечного метода.
Поскольку области устойчивости обоих уравнений
содержат левую полуплоскость, одношаговый двухточечный метод является А-устойчивым и, следовательно, может использоваться для
решения жестких систем.
ВЫВОДЫ
В результате проделанной работы показано, что явные методы Рунге-Кутта не являются A устойчивыми и не могут использоваться при решении жестких систем, поскольку требуют для устойчивости столь малого шага, что приводит к чрезвычайно большим затратам времени решения задачи.
Среди неявных методов Рунге-Кутта есть A-устойчивые методы. К ним относятся неявные методы первого и второго порядка точности. Методы более высоких порядков точности, хотя и не являются A-устойчивыми, однако могут быть использованы при решении жестких систем.
Средствами пакета Mathematica были получены программы для исследования устойчивости ряда методов решения задачи Коши для ОДУ.
В данной работе рассмотрены и изучены методы параллельного численного решения задачи Коши для ОДУ, ориентированные на вычислительные системы с различной параллельной архитектурой, описаны способы оценки погрешности.
Также были затронуты вопросы закономерности распараллеливания решения систем обыкновенных дифференциальных уравнений, описаны подходы получения расчетных коэффициентов различных методов с помощью пакета Mathematica.
ЛИТЕРАТУРА
- Воеводин В.В. Суперкомпьютеры: вчера, сегодня, завтра. // Сборник научно-популярных статей «Российская наука на заре нового века». Под редакцией академика В.П. Скулачева. – М.: научный мир, 2001. С. 475-483
- Левин Вл. К. Отечественные суперкомпьютеры семейства МВС. // http://parallel.ru
- Крюков В.А. Разработка параллельных программ для вычислительных кластеров и сетей. // http://parallel.ru
- Корнеев В. В. Параллельные вычислительные системы. – М.: Нолидж, 1999.
- Самарский А.А., Гулин А.В. Численные методы. – М.: Гл. ред. физ.-мат. лит., 1989. – 432 с.
- В.П. Гергель, Р.Г. Стронгин Основы параллельных вычислений для многопроцессорных вычислительных систем – Нижний Новгород, 2003
- Шнитман В. Современные высокопроизводительные компьютеры. Информационно-аналитические материалы Центра Информационных Технологий, 1996.
- Воеводин В.В., Капитонова А.П. Методы описания и классификация ВС – МГУ 1994
- Системы параллельной обработки: Пер. с англ./ Под. ред. Ивенса Д. – М.: Мир,1985 – 416с.
- Фельдман Л.П. Параллельные алгоритмы моделирования динамических систем, описываемых обыкновенными дифференциальными уравне-ниями. // Научн. тр. ДонГТУ. Серия: Информатика, кибернетика и вычисли-тельная техника, (ИКВТ-99) выпуск 6: – Донецк: ДонГТУ, 1999, с. 24-29.
- Фельдман Л. П. Сходимость и оценка погрешности параллельных одношаговых блочных методов моделирования динамических систем с со-средоточенными параметрами //Науковi працi Донецького державного тех-нiчного унiверситету. Серiя: Проблеми моделювання та автоматизації проектування динамичних систем, випуск 15: – Донецк:, 2000. С. 12-16.
- Воеводин В.В. Математические основы параллельных вычислений. – М.: Изд-во МГУ, 1991. – 345 с.
- Фельдман Л.П., Дмитриева О.А. Эффективные методы распараллеливания численного решения задачи Коши для обыкновенных дифференциальных уравнений.// Математическое моделирование, том 13, № 7, 2001. – С.66-72.
- Хайрер Э. Решение обыкновенных дифференциальных уравнений. М.: Мир, 1988.
- Дж. Холл, Дж. Уатт. Современные численные методы решения обыкновенных дифференциальных уравнений. М.: Мир,1979. – 312с.
|