| Автобиография |
| Ссылки |
| Отчет по поиску |
| Автореферат |
| Электронная библиотека |
| Индивидуальное задание |
| Домашний веб-сайт |
| Написать мне письмо |
| ДонНТУ Магистратура ДонНТУ |
|
|
|
Магистр ДонНТУ Хоменко В. Н.Разработка типовых моделей электромеханических систем для анализа возможных аварийных ситуаций в узлах производственных механизмовАвторефератАктуальность В настоящее время имеется необходимость в обеспечение эксплуатационной надёжности электромеханического оборудования, в проверке и определении его состояния без осуществления демонтажа, в прогнозировании технического состояния и обеспечение безопасности функционирования. Осуществление безразборной проверки основано на применении виброакустических методах диагностирования, тепловой диагностике, диагностике по электрическим величинам электропривода. В данном направлении методы виброакустической диагностики достигли наибольшего развития. Особенностью нашей работы является изучение взаимовлияния между электромеханическим преобразователем и приводимой нагрузкой, и поиск возможности извлекать диагностические признаки из электрических величин механизма (электрический ток, напряжение, мощность). Отечественный и зарубежный опыт показывает, что введение средств диагностирования является экономически оправданным. Известно, что вовремя выполненные ремонтные работы уменьшают возможность производственных травм, количество внезапных отказов оборудования, что соответственно уменьшает время остановки производственных линий. Цель работы Разработка математических моделей, которые позволят диагностировать аварийные ситуации в узлах производственных механизмов. Содержание работы Методам вибродиагностики для оценки технического состояния промышленного оборудования посвящены работы [1,2,3,4,6,7]. В материале [3] даны описания наиболее распространенных дефектов оборудования – приведены спектрограммы вибропараметров, наблюдающиеся при тех или иных неисправностях, описаны их отличительные особенности. В [6] автором рассмотрены вопросы улучшения и оптимизации технического состояния оборудования размольного отделения мельницы путём разработки и внедрения методов и средств функциональной вибродиагностики. Проведены теоретические и экспериментальные исследования. Даны ссылки на условия проведения поставленных экспериментов. Рассмотрены частотные математические модели следующих дефектов: «неуравновешенность ротора энтолейтора», дефект вальцевого станка «недостаточное усилие предохранительной пружины» и др. Приведены статистические данные влияния способа установки вибродатчика на значения различных параметров вибрации. Исследования проведены на вальцовом станке. В [8] приведены основы спектрального анализа на основе преобразования Фурье. Показаны достаточные условия существования прямого и обратного преобразования, описаны его основные свойства, рассмотрено оконное преобразование Фурье и приведены свойства некоторых функций окна. Таким образом, приведены характерные математические соотношения. В то время, как в литературе [5] делается упор на практическое применение средств обработки сигналов с применением системы MATLAB 6.5/7. Так же приведены основы работы с MATLAB и Simulink. Описаны функции и средства создания, обработки сигналов, их фильтрации, вейвлет-анализа. Наблюдаемый объект может находиться в одном из следующих состояний [1]:
Среди диагностируемых неисправностей различают следующие [3]:
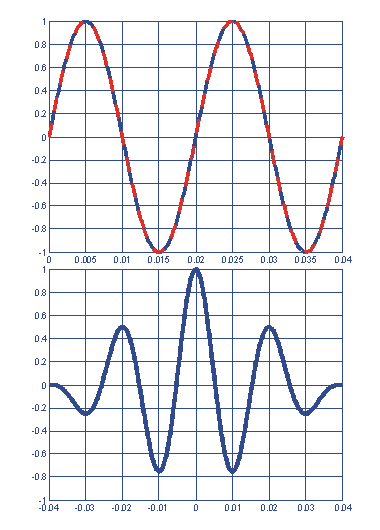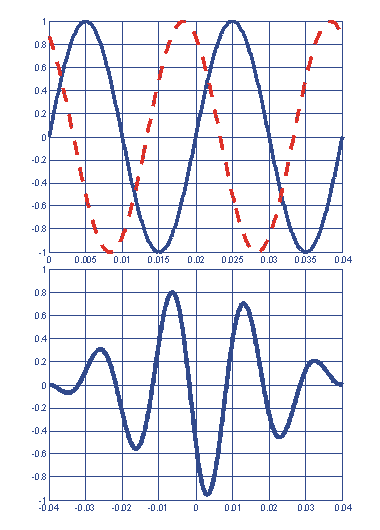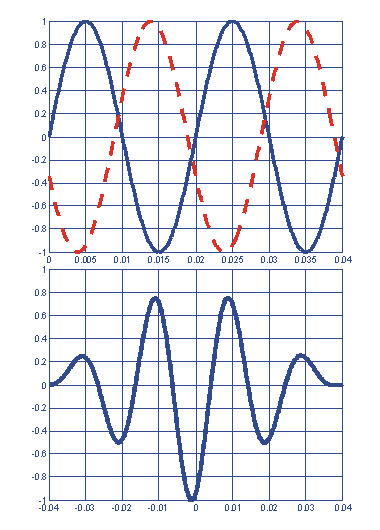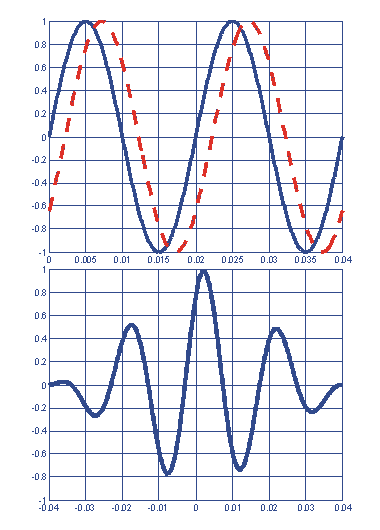
При диагностировании состояния электропривода все необходимые признаки извлекаются из наблюдаемых сигналов. Используются следующие характеристики сигналов: спектр, динамический спектр, кепстр, корреляция, автокорреляция, биспектр, бикогерентность, и вейвлет разложение. Применяют методы фильтрации сигналов, синхронного и синхронизированного детектирования, резонансного усиления, другие методы подавления помех и извлечения полезной информации. В этом случае применение теории и методов преобразования Фурье и вейвлет преобразования является перспективным. На следующем примере графически изображено поведение функции взаимной корреляции двух синусоидальных сигналов при вариации начальной фазы одного из них:
Преобразование Фурье, перенося представление сигнала из временной области в частотную, фактически разбивает сигнал на составные синусоиды, теряет временную информацию, и таким образом является применимым лишь для стационарных сигналов. Однако существуют методы, позволяющие получить дополнительно временную информацию. Применяют оконное преобразование Фурье, разбиение сигнала во временной области на части и др., но такие методы имеют явные ограничения. Прямое преобразование Фурье:
Обратное преобразование Фурье:
Вейвлет преобразование в свою очередь основано на вейвлетах - форме волны, имеющей ограниченную длительность и среднее значение равное нулю. Таким образом, вейвлет преобразование основано на разбиении сигнала на сдвинутые и масштабированные версии исходного (материнского) вейвлета.
где: Чтобы установить взаимосвязь между множеством состояний W на входе электромеханической системы и множеством диагностических признаков Z на выходе, необходимо иметь математическое описание этих соотношений с применением моделей электромеханических систем. В [1] показано: множество состояний W можно разбить на два подмножества: W` и W``. Подмножество W` включает в себя работоспособные состояния, позволяющие механизму выполнять возложенные на него функции. Каждое из состояний в этом подмножестве различается запасом работоспособности (приближение к предельно допустимому значению). Переход из одного состояния в другое в подмножестве W` может объясняться возникновением неисправностей, не приводящих к потере работоспособности (зарождающиеся дефекты). Подмножество W`` включает в себя состояния, соответствующие возникновению в механизме неисправности, приводящей к потери им работоспособности. Для того чтобы можно было поставить диагноз, все возможные состояния нужно разбить на некоторое конечное число m классов Wi; i=1, 2, … m, подлежащих распознаванию. Число классов в подмножестве неработоспособных состояний определяется числом возможных отказов. Такая классификация состояний объекта позволяет разделить процесс диагностирования на несколько этапов. На первом шаге определяют принадлежность объекта к одному из подмножеств W` или W``. Анализ состояний объекта в подмножестве W` позволяет определить характер изменений его работоспособности и в ряде случаев предсказать момент перехода в подмножество W``. На этом шаге возникают деградационные процессы в узлах механизмов и изменения в свойствах виброакустических сигналов. На третьем шаге определяют принадлежность объекта к одному из состояний подмножества W``. С целью исследования динамики сложных электромеханических систем, состоящих из большого числа расчетных масс, предлагается разбиение их на более простые подсистемы. В качестве базовой принимаем двухмассовою расчетную электромеханическую систему. В общем случае при проведении анализа следует учитывать такие ее параметры, как коэффициент жесткости С12 между двумя массами, коэффициент вязкого трения b12, различные нелинейности в виде зазора, переменного момента инерции и др. На поведение системы значительным образом влияют характер движущего момента и момента сопротивления. Определение взаимосвязи между видом воздействия на систему и реакцией системы позволит использовать ее в качестве диагностического признака. Идя от частного к общему, рассмотрим вначале основные соотношения на примере двухмассовой неразветвленной схемы. Положим, что b12=0 и система не содержит нелинейностей. Таким образом, двухмассовая ЭМС описывается следующей системой дифференциальных уравнений:
Задавшись собственной частотой колебаний
Для конкретной модели примем:
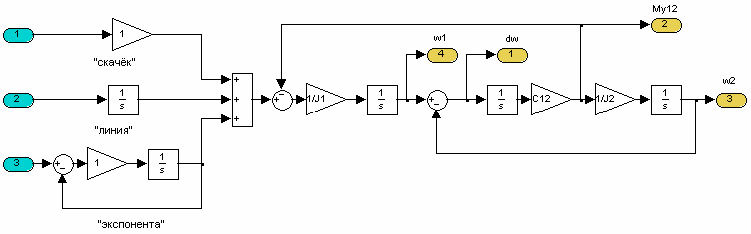
По уравнениям (1) составим модель системы.
Для данной модели (рассматривается ПФ
Из графиков видно, что на частоте Рассмотрим модели формирования трёх наиболее характерных сигналов:
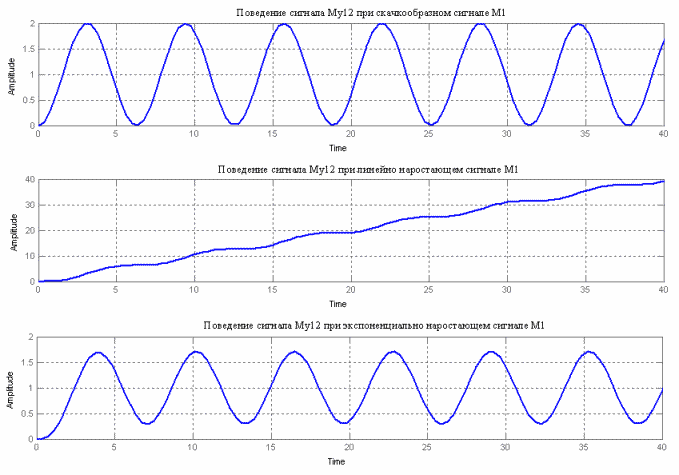
При подаче сигнала «единичный скачёк» на каждую из моделей, их выходной сигнал имеет вид, как показано на рис. 6.
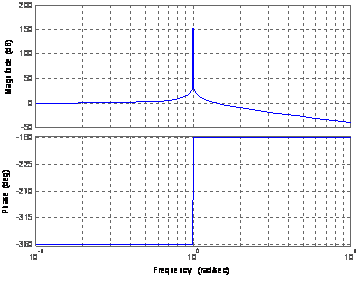
Данные модели могут быть использованы для моделирования более сложных сигналов, состоящих из нескольких частей. При этом необходимо в определенный момент времени переключиться на модель требуемого порядка и задать соответствующие начальные условия. Для каждой из моделей приведем ее ЛАЧХ, ЛФЧХ и ПФ.
Воздействие того или иного сигнала (из рассматриваемых нами) на 2х-массовую систему можно свести к воздействию сигнала «единичный скачёк» на систему, состоящую из двух частей: модели сигнала на входе (формирует М1) и непосредственно модели 2х-массовой системы.
Определим ПФ составной системы при различном характере управляющего воздействия. Для сигнала «скачёк» получаем:
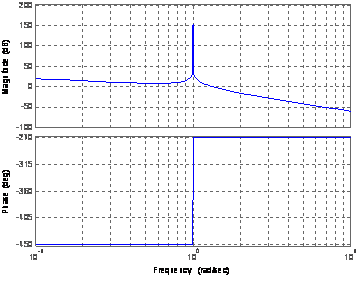
где Т.е. Для сигнала «линия»:
Таким образом, появляется сомножитель Для сигнала «экспонента»:
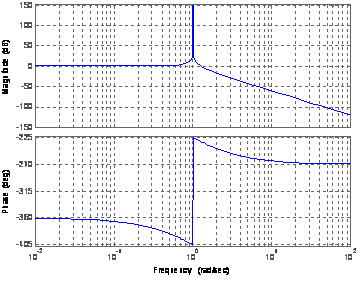
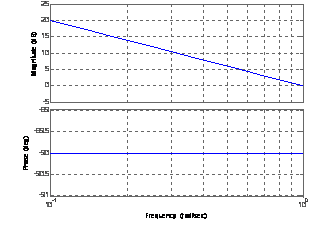
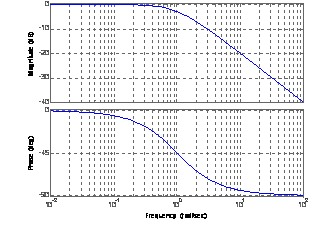
На частоте среза наклон ЛАЧХ увеличивается на -1. Претерпевает изменение ЛФЧХ (–pi/8 рад. на частоте среза, 0 рад. на октаву ниже и –pi/4 рад. на октаву выше). Приведенное иллюстрируется следующими зависимостями (для k=1, T=1).
Как видно из формул (2-4) и графиков (11-13), для модели составной системы ф-ла (2) характерно равенство нулю коэффициента демпфирования. Для модели ф-ла (4) характерно, что при увеличении постоянной времени Т увеличивается коэффициент демпфирования системы.
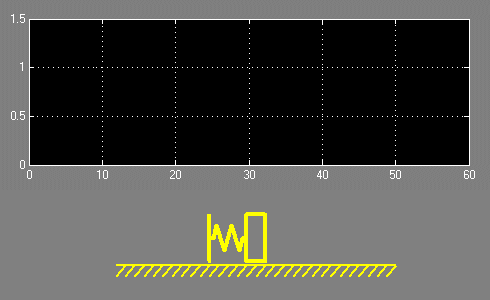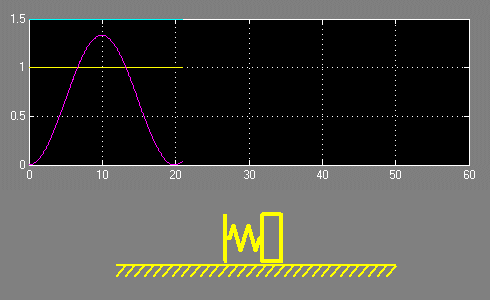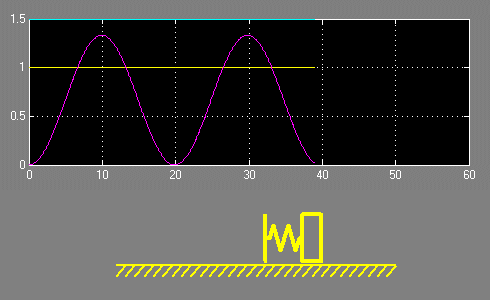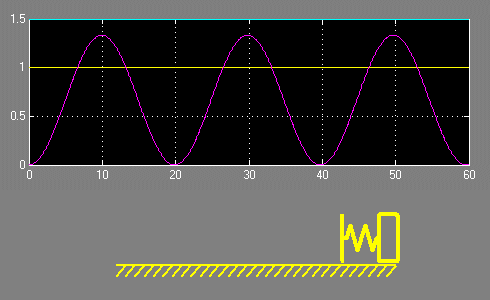
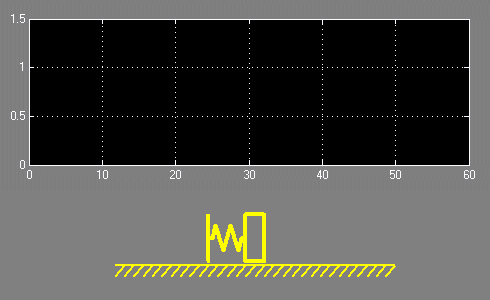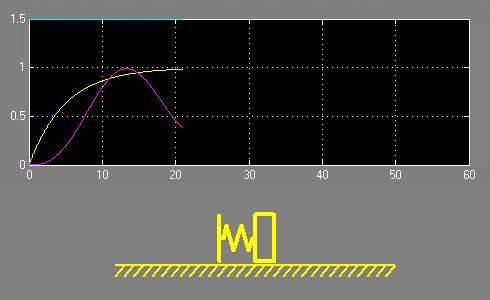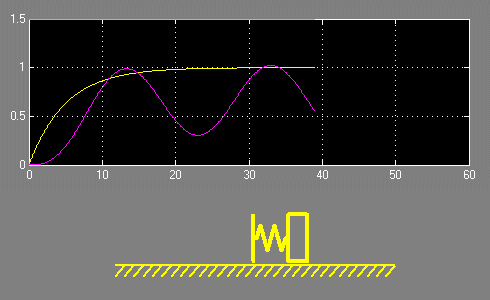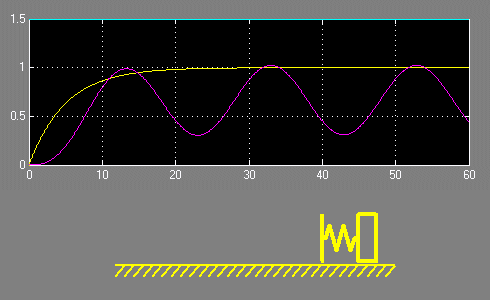
С целью наглядности проиллюстрируем эти зависимости с помощью анимации, отобразив также изменение положения первой и второй масс.
Заключение Применение типовых моделей для диагностирования электромеханических систем позволит автоматизировать процесс диагностирования, повысить точность постановки диагноза. Определение взаимозависимости между электрическими и механическими параметрами системы даст возможность диагностировать неисправности с меньшими трудозатратами. Литература
|
|
|
ДонНТУ > Магистратура ДонНТУ Автобиография | Ссылки | Отчет по поиску | Электронная библиотека | Индивидуальное задание |
|
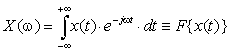
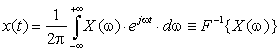
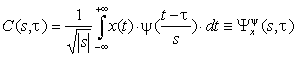
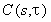 - вейвлет-коэффициенты, являющиеся функцией масштаба и положения;
- вейвлет-коэффициенты, являющиеся функцией масштаба и положения;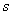 - масштаб вейвлета;
- масштаб вейвлета; 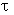 - положение вейвлета;
- положение вейвлета;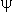 - вейвлет-функция.
- вейвлет-функция.
 , (1)
, (1)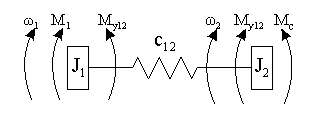
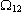 , моментами инерции системы J1 и J2, определим требуемую жесткость С12:
, моментами инерции системы J1 и J2, определим требуемую жесткость С12: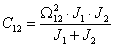
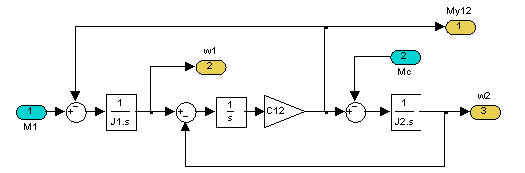
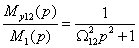 ) получены следующие ЛАЧХ и ЛФЧХ (рис.4).
) получены следующие ЛАЧХ и ЛФЧХ (рис.4).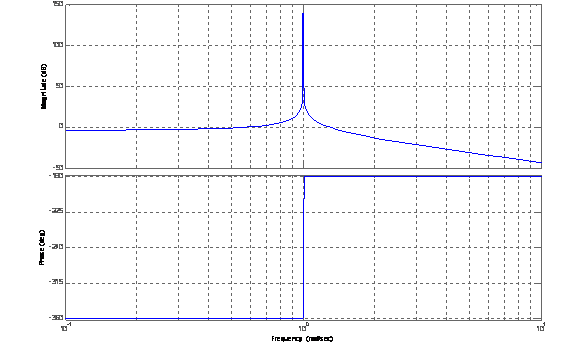
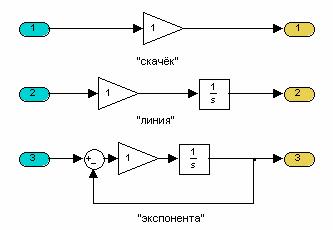
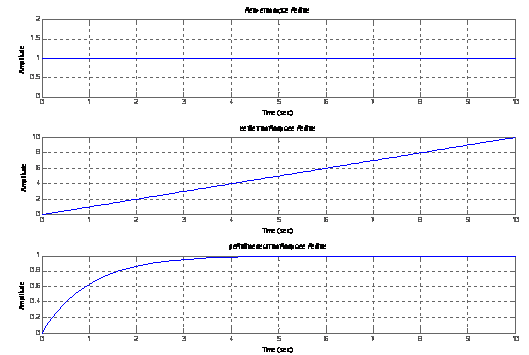

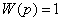
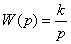
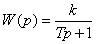
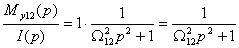 , (2)
, (2)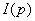 - изображение входного сигнала модели формирования сигнала М1.
- изображение входного сигнала модели формирования сигнала М1.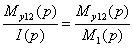 для сигнала М1 типа «скачёк».
для сигнала М1 типа «скачёк».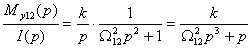 , (3)
, (3)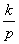 , что сказывается на ЛАЧХ, увеличивая ее наклон на -1. ЛФЧХ смещается на 90deg (–pi/2 рад).
, что сказывается на ЛАЧХ, увеличивая ее наклон на -1. ЛФЧХ смещается на 90deg (–pi/2 рад).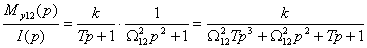 , (4)
, (4)