Автореферат |
|
| Введение. Актуальность темы |
|
Современный этап развития нашей страны отличается динамизмом и качественными изменениями во всех сферах общественной жизни. Такая ситуация ставит высокие требования к умению руководителей управлять предприятием при наличии большого количества конкурентов, которые уже имеют соответствующие знания и практику управления предприятием в этих условиях. Поэтому одной из важнейших проблем является проблема управления современным предприятием в новых, рыночных условиях, которые быстро меняются. Очевидно, что традиционные методы управления оказываются недееспособными в новых для страны условиях. Необходимо определиться с соответствующим подходом к управлению предприятиями. Экономико-математическое моделирование, являясь одним из эффективных методов описания сложных социально - экономических объектов и процессов в виде математических моделей, превращается тем самым в часть самой экономики, вернее, в сплав экономики, математики и кибернетики. Модели, как правило, строятся на основе статистических данных. Статистика позволяет компактно описать данные, понять их структуру, провести классификацию, увидеть закономерности в хаосе случайных явлений. Удивительно, что даже простейшие методы визуального и разведочного анализа данных позволяют существенно прояснить сложную ситуацию, первоначально поражающую нагромождением цифр. В экономических исследованиях часто решают задачу выявления факторов, определяющих уровень и динамику экономического процесса. Такая задача чаще всего решается методами корреляционного, регрессионного, факторного и компонентного анализа. Взаимодействие главных и второстепенных факторов и определяет колеблемость исследуемого процесса. В этом взаимодействии синтезируется как необходимое, типическое, определяющее закономерность изучаемого явления, так и случайное, характеризующее отклонение от этой закономерности. Случайные отклонения неизбежно сопутствуют любому закономерному явлению. Для достоверного отображения объективно существующих в экономике процессов необходимо выявить существенные взаимосвязи и не только выявить, но и дать им количественную оценку. Этот подход требует вскрытия причинных зависимостей. Под причинной зависимостью понимается такая связь между процессами, когда изменение одного из них является следствием изменения другого. Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение результативного признака обуславливается влиянием одного или нескольких факторных признаков, а множество всех прочих факторов применяется за постоянные (или усредненные) величины. Очень часто регрессионный анализ является базой при построении математических моделей прогнозирования производственных процессов. Преимущество таких моделей состоит в том, что они позволяют оценить так называемые гипотетические варианты ситуации. При выборе вида регрессионного уравнения идет речь только об аппроксимации относительно простыми функциями несравненно более сложных по своей природе взаимосвязей. На практике отдают предпочтение линейным моделям или приводят модели к линейному виду путем преобразования переменных, например логарифмированием. Такой подход, безусловно, содержит в себе определенную условность, поскольку предусматривает одинаковый характер связи со всеми факторами. Однако использование слишком сложных функций неизбежно ведет к увеличению количества параметров, а, следовательно, уменьшает точность измерения и усложняет интерпретацию результатов. |
| Цель и задачи работы |
|
Одной из главных целей функционирования любого промышленного предприятия является получение максимальной прибыли, что всегда сопряжено с необходимостью совершенствования организации производства. Применяемые в настоящее время на отечественных предприятиях методы планирования, организации и управления производством продукции часто являются экономически не обоснованными и, как следствие, не дают ожидаемого экономического результата. Объем производства продукции становится важнейшим объектом управления, существенно возрастает роль планирования, анализа и обоснования управленческих решений, применяемых на предприятии для стабилизации или роста объема выпуска. В связи с этим вопросы установления оптимального объема производства приобретают первостепенное значение не только с позиций необходимости получения предприятием максимума прибыли, но и с позиций эффективного управления предприятием в целом и его структурными подразделениями. Таким образом, целью магистерской работы является оптимизация объемов производства на промышленном предприятии. Оптимизация проводится на основе классической задачи оптимизации объема производства предприятий, которые выпускают однородную продукцию. Оптимальным является такой объем производства продукции, при котором суммарные удельные издержки минимальны. Однако данная задача решена не до конца и является в большей мере теоретической. В связи с этим планируется уточнить критерий оптимизации, оценить точность оптимизации, которая определяется доверительным интервалом. |
| Обзор существующих исследований и разработок |
|
Управление объемом производства является достаточно сложным процессом. Его оптимизация фактически означает совершенствование управления всей деятельностью предприятия, так как охватывает все стороны функционирования этого объекта управления. Для эффективного управления затратами на производство продукции необходимо располагать информацией о внешней среде предприятия, внутренней деятельности предприятия, перераспределять на этом уровне материальные, технические и трудовые ресурсы. Анализ состояния вопроса определения оптимального объема производства в научной литературе и в практике производственно-хозяйственной деятельности предприятий показал, что теория и методология его формирования требует существенной доработки. Объем производства и предложения товаров определяется технологическими и экономическими условиями работы производителей. В существующих к настоящему времени работах ученых-экономистов, как правило, рассматривается максимизация прибыли на основе производственных функций. В них определяется зависимость между реальными (физическими) объемами используемых в производстве ресурсов и максимально возможным при этом выпуском продукции. Сущность предлагаемых авторами методов определения оптимального объема производства заключается в следующем. Объем выпуска, максимизирующий прибыль, зависит от технологических и экономических условий функционирования предприятия. Первые отображаются кривой общего выпуска, а экономические условия представляются в виде линии равной прибыли. Каждая точка линии прибыли указывает на такое сочетание объема производства и ресурсов, которое обеспечивает заданный объем прибыли. Каждому объему прибыли соответствуют определенные технологические и экономические условия. Наложение карты линий прибыли на кривую общего выпуска совмещает технологические и экономические условия работы предприятия. Точка касания таких линий определяет объем выпуска, максимизирующий прибыль в сложившихся условиях. Однако предложенный подход к определению максимума прибыли является в большей мере теоретическим. Большинство производственных функций представляют собой зависимость объема производства от затрат труда и капитала. Данные факторы, безусловно, являются основополагающими, однако далеко не единственными. Процесс определения оптимального объема производства продукции является задачей многокритериальной и много вариантой. Существенно повысить эффективность работы предприятия представляется возможным только на основе обоснованного критерия оптимизации, а также необходимо найти доверительные интервалы объема выпуска, поскольку производство является инерционным. |
| Предполагаемая научная новизна и практическая ценность |
|
Применяемый подход к оптимизации объема производства продукции является в большей мере теоретическим и не имеет практического смысла, поскольку в связи с инерционностью производства оптимальный объем продукции является многовариантным и руководитель никогда не сможет произвести ровно столько продукции, сколько предполагает данная модель. Для реализации поставленной задачи на практике необходимо расширить интервал оптимального объема производства, что и будет выполнено в ходе работы. |
| Текущие результаты |
|
Применимость регрессионных моделей в прогнозировании |
|
Особенностью процессов организации, планирования и управления на промышленных предприятиях в общем случае является необходимость принятия решений при огромном многообразии производственных ситуаций. При этом процессы принятия решений имеют две основные черты. Во-первых, принятие решения связано с выбором из множества решений, допускаемых обстоятельствами, некоторого одного, вполне определенного. То есть, всегда имеется множество вариантов принятия решения. Во-вторых, принятие решения всегда производится во имя той или иной цели и должно в наибольшей степени ей соответствовать. В связи с этим необходимо количественно оценить степень осуществления цели при каждом варианте решения. Таким образом, необходимо, чтобы каждый процесс принятия решений был описан функцией, аргументами которой являются допустимые варианты решения, а значениями - числа, которые описывают меру достижения поставленной цели. Эту функцию принято называть целевой функцией, критерием оценки, или показателям эффективности. Описание множества допустимых решений и целевой функции является математическим моделированием явления. Задача принятия решения сводится к нахождению максимального (или минимального) значения целевой функции, а также к нахождению того конкретного решения - аргумента, при котором это значение достигается. Такое решение называется оптимальным. Принятие решений при планировании и управлении производством, как правило, требует использования специального математического аппарата. Математические методы можно условно разделить на два класса: вероятностные и детерминированные. К вероятностным методам относятся регрессионный анализ, теория случайных функций, различные методы прогнозирования, теория игр, теория принятия решений, имитационное моделирование и др.; к детерминированным - матричные методы, линейное, нелинейное программирование, потоки в сетях, динамическое программирование и др. "Регрессионный анализ - это основной метод современной математической статистики…." Так оценили роль регрессионного анализа отечественные ведущие специалисты в области прикладной математической статистики Ю. Адлер и В. Горский. Очень часто регрессионный анализ является базой при построении математических моделей прогнозирования производственных процессов. Регрессионная модель описывает объективно существующие между явлениями корреляционные связи. По своему характеру корреляционные связи необычно сложны и разнообразны. Отследить все эти взаимосвязи и установить точный функциональный вид практически невозможно. Поэтому при выборе функции идет речь только об аппроксимации относительно простыми функциями несравненно более сложных по своей природе взаимосвязей. На практике отдают предпочтение линейным моделям или приводят модели к линейному виду путем преобразования переменных, например логарифмированием. Такой подход, безусловно, содержит в себе определенную условность, поскольку предусматривает одинаковый характер связи со всеми факторами. Однако использование слишком сложных функций неизбежно ведет к увеличению количества параметров, а, следовательно, уменьшает точность измерения и усложняет интерпретацию результатов. В общем виде парная модель регрессионного анализа имеет вид: |
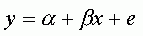
|
|
где a - свободный член уравнения, определяет область существования модели; b - выборочный коэффициент регрессии, отражает влияние фактора x на результативный признак y , т.е. показывает на сколько единиц в среднем изменяется результативный признак y при изменении факторного признака x на единицу; e - случайная переменная, характеризующая отклонение от теоретической линии. Соотношения между социально-экономическими явлениями не всегда можно описать линейной регрессией. В этом случае используют нелинейную регрессию, причем конкретный вид может быть определен по облаку рассеиванию, из опытов предыдущих исследований, из содержания задачи. Аналитически нелинейная взаимосвязь между двумя величинами может быть описана следующим образом: - параболическая регрессия |
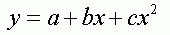
|
|
- гиперболическая регрессия |
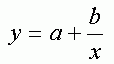
|
|
- полиномиальная регрессия |
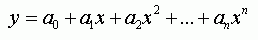
|
|
- гармоническая регрессия |
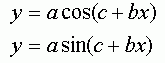
|
|
- экспоненциальная |

|
|
Можно привести множество примеров из различных областей экономической деятельности, когда регрессионные уравнения оказались хорошими измерителями взаимосвязи явлений. Например, известен целый ряд работ, посвященных измерению зависимости производительности труда в различных отраслях производства и на отдельных предприятиях от соответствующих факторов субъективного и объективного характера (стаж, квалификация рабочего и т.д.). Часто с помощью регрессионного анализа оценивают взаимосвязи результатов хозяйственной деятельности с различного рода факторами (размерами капитальных вложений, возрастом оборудования и т.д.). Известны удачные примеры применения регрессий для характеристики стоимости создания какого-либо изделия, например самолета, в зависимости от его технико-эксплуатационных параметров. На основе соответствующих регрессий прогнозировались затраты на ремонт отдельных узлов самолетов в зависимости от таких факторов, как число летных часов и число неполадок в прошлом. Именно способность регрессионного уравнения отобразить взаимосвязь между явлениями нашла себе практическое применение в прогностическом анализе. К регрессионным моделям прибегают и как к вспомогательному средству в комплексной методике прогнозирования (например, в рамках разработки прогностической межотраслевой модели производства и распределения продукции регрессии используются для оценивания отдельных компонентов конечного продукта), и как к самостоятельному инструменту прогноза. Регрессионный анализ предполагает решение двух задач. Первая заключается в выборе независимых переменных, существенно влияющих на зависимую величину, и в определении формы уравнения регрессии (обычно этот этап в разработке регрессии называют спецификацией). Данная задача решается путем анализа изучаемой взаимосвязи по существу. Формальные средства могут служить здесь лишь некоторыми ориентирами. Вторая задача - оценивание параметров - решается с помощью того или иного статистического метода обработки данных наблюдения. Наиболее часто оценивание параметров регрессий достигается с помощью метода наименьших квадратов. |
|
Экономико-математическое решение поставленной задачи |
|
В экономико-статистических моделях, как и в оптимизационных, большое значение имеет правильный выбор критерия оптимальности. В каждом конкретном случае необходимо обосновать его слагаемые. Рассмотрим классическую задачу оптимизации объема производства предприятий, которые выпускают однородную продукцию. Чаще учитываются такие слагаемые, как себестоимость, транспортные расходы и удельные капиталовложения. В этом случае критерий для определения оптимального размера производства будет иметь следующий вид: |
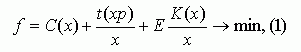
|
|
где C(x) - функция, учитывающая зависимость себестоимости продукции от мощности предприятия; x - искомая мощность предприятия; p - плотность сырья в зоне расположения предприятия, т.е. количество товарного сырья, приходящегося на квадратный километр площади; t(xp)/x - функция, учитывающая зависимость удельных транспортных расходов от мощности предприятия и плотности сырья; E - нормативный коэффициент эффективности капитальных вложений в отрасли; K(x)/x - функция, отражающая зависимость удельных капитальных вложений от мощности предприятия. Возьмем пять предприятий с различным объемом производства однородной продукции, и выпишем их основные отчетные показатели (табл.1). |
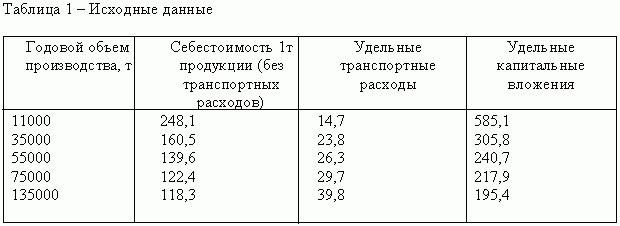
|
|
Для расширения круга альтернативных вариантов предприятий определим модели, характеризующие зависимость себестоимости продукции, транспортных расходов и удельных капитальных вложений от объема производства. Сначала определим характер зависимости от объема производства первого элемента критерия - себестоимости единицы продукции C(x). Для этой цели построим график, характеризующий данную зависимость (рис.1). |
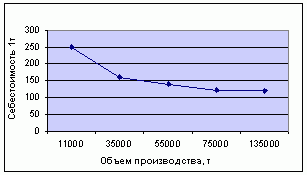
|
|
Рисунок 1 - Зависимость себестоимости единицы продукции от объема производства Как видно, эмпирическая линия регрессии по своему характеру близка кривой типа гиперболы и описывается уравнением: |
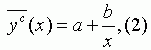
|
|
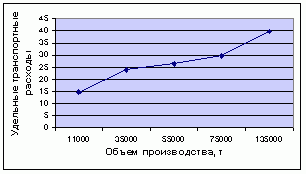
Далее перейдем к определению модели для расчета показателе второго слагаемого критерия оптимальности - удельных транспортных расходов t(xp)/x . Для этого изобразим графически зависимость транспортных расходов от объема производства (рис. 2) |
|
|
Рисунок 2 - Зависимость удельных транспортных расходов от объема производства Графически зависимость транспортных расходов от объема производства близка к линейной и описывается уравнением: |
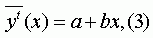
|
|
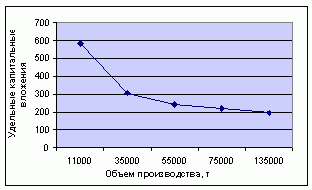
В заключении определим модель для расчета показателей третьего слагаемого критерия оптимальности - удельных капитальных вложений K(x)/x. Графическая зависимость удельных капитальных вложений от размеров производства показана на рис. 3. |
|
|
Рисунок 3 - Зависимость удельных капитальных вложений от объема производства Эмпирическая линия регрессии по своему характеру близка к кривой типа гиперболы и описывается уравнением: |
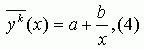
|
|
Для определения параметров полученных уравнений воспользуемся МНК, следовательно, конкретные экономико-статистические модели будут следующими: |
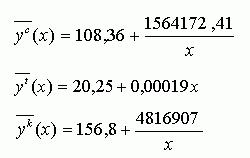
|
|
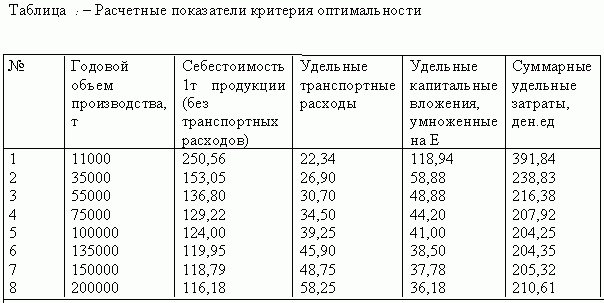
Итак, теперь получены все необходимые данные, чтобы по принятому критерию оптимальности рассчитать суммарные удельные затраты по всем возможным вариантам развития предприятий, в ключая и гипотетические, которых в действительности пока нет. Заметим, что в таблицу включаются только расчетные показатели себестоимости, удельных транспортных расходов и капиталовложений. Причем последний показатель умножается на 0,2 (Е) - нормативный коэффициент эффективности капиталовложений. |
|
|
Описанные выше этапы комплексно представлены на следующем рисунке. |
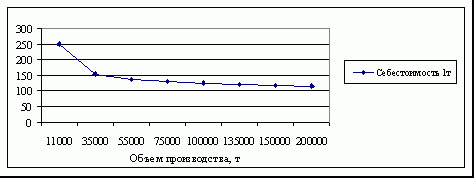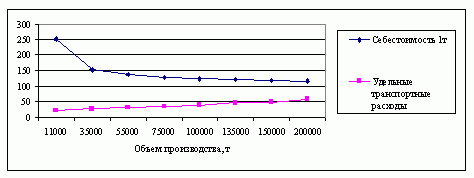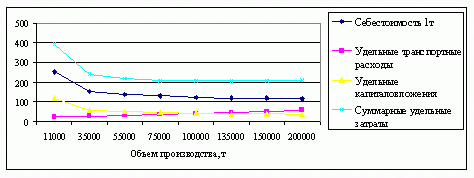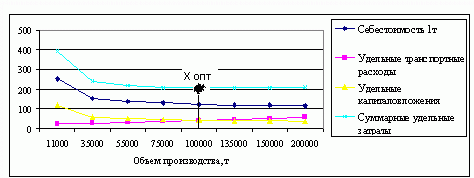
|
|
Анимированный рисунок - Методика определения оптимального объема производства Исходя из даннях табл. 2 оптимальным является вариант предприятия мощностью в 100000 т. Суммарные удельные затраты здесь составляют 204,25 ден.ед. Далее они начинают возрастать. Однако следует обратить внимание на два обстоятельства. Во-первых, незначительная раз ница в суммарных затратах по 5 и 6 вариантам и, во-вторых, большое различие в мощности предприятий по этим вариантам. Потому возникает необходимость апробирования вариантов, скажем, в 110б 120 и 130 тыс. т продукции. По этим вариантам суммарные удельные затраты соответственно составляют 203, 85, 203,83 и 193,85 ден.ед. Следовательно оптимальным будет предприятие с объемом производства в 130000 т. Суммарные затраты на тонну продукции на этом предприятии в два раза ниже, чем на первом с объемом производства в 11000 т и на 8% ниже, чем у наиболее крупного предприятия с объемом производства 200000 т. Однако в связи с инерционностью производства оптимальный объем продукции является многовариантным и руководитель никогда не сможет произвести ровно столько продукции, сколько предполагает данная модель. Для реализации поставленной задачи на практике необходимо расширить интервал оптимального объема производства, т.е. определить доверительный интервал. Для этого определяется доверительный интервал для функции себестоимости, удельных транспортных и капитальных вложений. После чего переходят к обратным функциям, т.е. определяется зависимость мощности предприятия от себестоимости продукции, удельных транспортных и капитальных вложений. Подставляя выше полученные значения доверительных интервалов в функции, получаем нижнее и верхнее значение интервала для оптимального объема производства. |
| Заключение |
|
Основным результатом является выбор экономико-математической модели определения оптимального объема производства продукции. Немало важным является и правильный выбор критерия оптимальности. В каждом конкретном случае необходимо обосновать его слагаемые. Проведенный анализ позволяет говорить, что оптимизация производства является важнейшей задачей работы предприятия. Однако планированию оптимального объема производства должен предшествовать детальный анализ технико-экономических показателей работы предприятия, который позволит оптимизировать параметры производственного процесса. Объем выпуска продукции зависит как от факторов внутренней среды, формируемой на предприятии, так и от факторов внешней среды. Эти факторы должны представляться в виде ограничений, которые необходимо учитывать в процессе разработки плана производства. |
| Список источников |
|
|
ПРИМЕЧАНИЕ:
|