FRACTAL PROPERTIES OF MICROGEOMETRY

OF PROCESSED SURFACES

Research manager: Ph.D.  Dr.  Matviyenko  Andriy

 

 

As it is known creation of surfaces with the certain microgeometrical properties is one of the primary goals of mechanical engineering. Especially it concerns surfaces of particularly responsible products of avia-space technics, instrument making, precision machine-tool construction, etc. Moreover, the question of maintenance of microgeometry of a surface is especially actual at development of new technologies of processing of surfaces both mechanical, physical and chemical ways of processing in the field of micro-and nanotechnology.

Quality of a surface is traditionally characterized by a roughness – an arithmetic mean deviation, the maximal height of roughness, average step of roughness of a structure, etc. and physicomechanical properties of a superficial layer []. The roughness of a surface, as many researchers have shown, is one of the basic parameters of quality of a surface. In many cases the microgeometry of a superficial layer predetermines behaviour of a surface during its operation, and in case of micro- and nanotechnology the roughness is considered not as secondary structure, but as a property of the structure of material.

As a rule, the microgeometry of a superficial layer is considered as a certain static object which was generated during some influence. Classically in processing of materials by cutting the roughness is a geometrical prototype of a trajectory of moving of the tool which is set by kinematics and modes of processing. On the other hand in the processing power, temperature and other fields are formed, there is a chemical influence on a surface, there are high pressures in a zone of contact of the tool and a processable surface, movement of dispositions, etc. owing to what the structure of a superficial layer changes. Therefore formation of a surface on the whole and microgeometry in particular is a result of action of set of processes and not just merely geometrical "responses" of action of the tool as for example it is marked in the work [2].

Within the limits of the considered concept of "collective" formation of a roughness it is possible to tell that such object as the microgeometry of a surface is dynamic system. Studying of dynamic system assumes studying of its properties which are defined by some people invariants (for example, Lyapunov's parameter, entropy, etc.). Therefore in this case the use of classical geometrical parameters of a roughness is insufficient or simply impossible. Moreover, geometrical parameters do not display such important property of roughness as dynamic system – evolution.

Thus, new approaches in an estimation of microgeometry of a surface are necessary and one of such approaches can be a use of the theory of fractals. Application of the theory of fractals will allow bringing of a new parameter for an estimation of a roughness, to create base not only for fractal classifications, but forecasting of change of microgeometry during its formation, both at a stage of processing by technological method, and at a stage of operation. The purpose of the given work is check of the introduced assumptions from positions of the theory of fractals on an example of formation of microgeometry of a surface at a stage of technological influences.

Brief positions of the theory of fractals

In general fractal is a geometrical object (a line, a surface, a spatial body) described by irregularity (structures, geometry, etc.), but self-similarity (or symmetry). Self-similarity means that the object more or less is uniformly arranged [3,4]on various scales of its consideration. That is the invariance of the basic geometrical features of object is supposed at the change of the scale.    For example, in figures formation(education) фрактальных objects is shown by a method of iterations.

 

                         

         http://www.cs.wisc.edu/~ergreen/honors_thesis/examples.html

Naturally there are borders of these scales connected with concept of final "weight" of object. The irregularity of object, in general, means its some fractional dimension distinguishing it from dimension of a line, a surface or space. Therefore in the theory of fractals concepts of topological dimension are used so-called Hausdorf-Bezikovich’s dimension which characterize "deviations" of a fractal (object) from ideal topology. Thus, fractals can be considered as set of the points enclosed in space.

Fractal dimension is one of the basic characteristics of a fractal. The central place in definition of fractal dimension D (Hausdorf-Bezikovich’s dimension) borrows concept of distance between points in space. Hence, for definition D it is necessary to measure "size" of set of points in space. The simple way to measure length of curves, the area of surfaces or volume of a body is to divide a body into small pieces, rectangulars, cubes or spheres. Counting up number of these elements which are necessary for a covering of required set of points, we receive a measure of size of set.

Fractal geometry is based on the experimental fact, that generally the length L of any curve (which can be broken in any point) in the sedate image depends on scale of measurement:

L = C⋅δ^1-D

where C is a dimensional multiplier for each curve, D - fractal dimension.

Other characteristic of fractals is correlated dimension. Correlated dimension D₂ is defined by a ratio [26, 28]:

,

where p_i² is probability of at random taken point which belongs to i-th cell (cube).

- the minimal number of n-dimensional cubes with an edge e, which are necessary for a covering of geometrical object.

Correlation dimension can be presented in the form of [4]:

,

where I (e) – the pair correlation integral defined from expression:

,

where Q() – Heviside’s function;

r_n, r_m – radiuses-vectors of pair of points n and m respectively.

The paired correlated integral defines probability of that two at random taken points are divided by distance which is smaller than e. Besides

i.e. fractal dimension D₂ defines dependence of paired correlated integral from e.

Thus, dimension D₂ is defined by the value of correlated integral describing relative number of pairs of points (n, m), removed on distances smaller e.

The following characteristic of fractal properties of object is correlated entropy or information dimension which to some extent considers frequency of hit of a point of set in an element of splitting of object. Numerical value entropy is the quantitative characteristic of a degree of a chaotic state of system.

Correlates entropy D₁ is defined from the following expression [4]:

,

where  - entropy of fractal sets,

 - probability of a finding of a point of object in i-th cell of splitting of object.

Correlated entropy can be calculated through correlated integral.

As a rule, a definition of correlated dimension and entropy is carried out for multifractals – non-uniformed fractal objects which have not only geometrical, but also statistical characteristics. In other words non-uniformed fractals have non-uniformed distribution of points of set or different density of "population" of set. Therefore during the research of multifractals they speak about generalized fractal dimensions [3,4] which can be presented above mentioned fractal dimensions. But in connection with special specificity of multifractals for the analysis the function of multifractal spectrum or a spectrum of a multifractal singularity is used. As it is mentioned in the work [4], the size of function a multifractal spectrum is actually equal to Hausdorff’s dimension (D) of some homogeneous fractal subsets from initial set which gives the dominating contribution to statistical characteristics of set. Therefore in the first approximation it is possible to consider, that D is fractal dimension concerning homogeneous fractals in multifractal set.

Thus, to the basic characteristics of a fractal belongs its dimension generalized or Hausdorff’s D, correlated D₂ and informative D₁.

Hurst 's parameter

There are various ways of defining of fractal dimensions to a number of which the so-called R/S-way belongs, on the basis of which Hurst 's parameter is defined [3]. This parameter has wide application in the analysis of time series owing to the remarkable stability. It contains the minimal assumptions of studied system and can classify time series. It can distinguish a random series from not random, even if a random series is not Gaussian’s one (that is not normally distributed).

For comparison of various types of time series Hurst has entered a following ratio:

R/S=(a·N)^Н,

where R/S – normalized scope from the saved up average, N – number of supervision, and – some constant, Н – Hurst 's parameter.

There are three various classifications for Hurst 's parameter:

1) Н = 0.5. Specifies a random series. Events are random and uncorrelated. The present does not influence the future. Function of density of probability can be a normal curve, however it is not obligatory condition. The R/S-analysis can classify any series, irrespective of what kind of distribution corresponds to it.

2) 0 ≤ Н< 0.5. The given range corresponds to antipersistent or ergodic series. Such type of system is often called – «return to an average». If the system shows "growth" during the previous period, most likely, in the following period recession will begin. And on the contrary, if there was a decrease close rise is probable. Stability of such antipersistent behaviour depends on how much Н is close to zero. Such series is more inconstant than random series as it consists of frequent reversers of recession-rise.

3) 0.5 <Н <1.0. We have persistent, or trend stable series. If a series increases (decreases) during the previous period it is probable, that it will keep this tendency for some time in the future. More Н is closer to 0.5, noisier a series is and less its trend is expressed. Persistent series is the generalized Brown’s movement, or the displaced casual wanderings. Force of this displacement depends on how much Н is more than 0.5.

The fourth characteristic of a parameter of Hurst also exists, when Н>1. In this case they speak about Levi statistics and about process (or a time series) with fractal time, about time points of break of a derivative. It means that there are independent jumps of amplitude distributed on Levi in time, certain in the size of jump, and growing together with it. The dispersion of an increment for the given interval of time becomes final, the trajectory in phase space keeps the kind, but new fractal object appears - time points of break of a derivative.

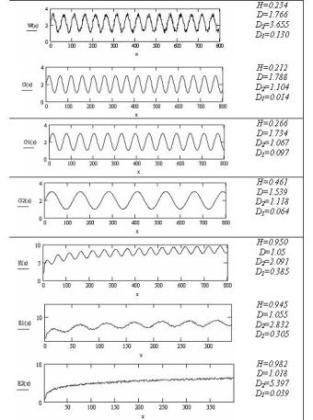
If in double logarithmic coordinates to find inclination R/S as function from N we shall receive grade N.  This grade is not connected with any assumptions concerning underlying distribution though in the work [5] attempt of classification of casual distributions on the basis of fractal scales is undertaken.

For very plenty of supervision N it is possible to expect convergence of series to size Н=0.5 as the effect of memory decreases up to that level when it becomes imperceptible. In other words, in case of some supervision it is possible to expect, that its properties become indistinguishable from properties of usual Brown’s movement, or simple casual wandering as the effect of memory dissipates.

Hurst 's parameter can be transformed in fractal dimension D by means of the following formula [3-5]:     

D=2-H

Fractal dimension of time series, or the saved up changes at casual wandering, is 1.5. Fractal dimension of a curve is 1, and fractal dimension of a geometrical plane is 2. Thus, fractal dimension of casual wandering lays between a curve and a plane. If Н = 0.5, D = 1.5. Both sizes characterize independent casual system. The size 0.5 <Н 1 will correspond to fractal dimension closer to a curve. It is persistent time series, giving more smooth, less jagged line, rather than casual wandering. Antipersistent size Н (0 <Н <0.5) gives accordingly higher fractal dimension and more faltering line, than casual wandering, and, hence, characterizes the system more subject to changes.

For an example on рис.1 schedules of various functions with Hurst 's parameter (H), fractal dimension (D), correlation dimension ₍D₂₎ and correlated entropy ₍D₁₎ are presented.

Fig.1. Fractal characteristics of functions

 

From resulted fractal characteristics it is easily possible to track their change on change of the form of schedules of functions. So, «noisier» functions by their fractal characteristics differ from ideal. For example, functions W (x) and G (x) which are described by identical expressions, but in W (x) a noisy component is added and distributed evenly on an interval [0-0.5]. If to consider, for example, sinusoidal functions G (x), G1 (x) and G2 (x) it can be noticed that with increase of the period of function Hurst 's parameter comes closer to Н=0.5.

It says about "approach" of function to a straight line, i.e. the sinusoid "is extended" in a straight line. Functions Е(х), Е1(х) and Е2 (х) are typical representatives of persistent series. Noise in Е2 (х) is insignificant in comparison with the general trend stability, therefore parameter Н is more than for functions Е (x) and Е1 (x) where not only trend stability but also periodicity are obviously expressed. And obviously various periods lightly influence the change of parameter Н in comparison with functions G (x), G1 (x) and G2 (x). Function A (x) represents casual wandering argument that parameter Н displays close to 0.5.

Thus, from the given examples the interrelation between a kind of function (time series) and Hurst 's parameter which says about an opportunity of its use for classification of functions (series) is visible. Meanwhile, there is one more feature of definition of a parameter of Hurst . As it was marked above for its definition it is necessary to approximate straight line R/S as function from N in double logarithmic coordinates. But thus, as a rule, characteristic sites of function log [R/S (N)] are not allocated and approximation is carried out so-called «Averaging ». For example, for function W (x) we have Hurst 's precisely specifying periodicity (ant persistence) but nothing speaking about a casual component which is not essential in comparison with obviously expressed periodicity. For revealing such prominent features of functions (time series) it is expedient to carry out approximation not on "average" of function log [R/S (N)], and on characteristic sites of this function. For example, on fig. 2 the schedule of function log [R/S (N)] (in figure the quantity of supervision or readout N is designated through t), constructed on function W (x) where two characteristic sites are confirmed to approximations.

 

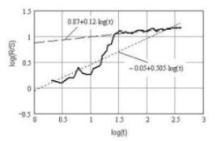
Fig.2. The schedule of function log [R/S (t)] for W (x) and its approximations

 

Apparently from figure two characteristic sites are well approximated by corresponding straight lines which specify Hurst 's parameters 0.12 and 0.505 that corresponds to periodicity and noisiness of function W (x).

 

Fractal characteristic of microgeometry of a superficial layer

For studying fractal characteristics of microgeometry of a superficial layer Talyrond traces were used, received after various kinds of mechanical influence on a processable surface of steel preparations. Fractal dimension of Talyrond traces was estimated under the characteristics resulted above: Hurst 's parameter, correlation dimension and correlated entropy. Hurst 's parameter was defined as on "averaging" all arguments (length of Talyrond traces) and on characteristic sites of function log [R/S (t)].

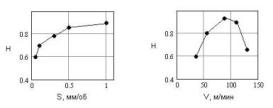
To more detailed researches Talyrond traces were exposed, received after processing turning on various modes of submission and speed of cutting.

On Fig.3 schedules of dependences of Hurst ’s parameter of a microstructure of the surface are presented and calculated on "averaging" of function log [R/S (t)], from submission and speed of cutting. Apparently from figure, parameter Н is in a range 0.5...1 that specifies on persistence of Talyrond trace. On some modes of processing casual wandering a microstructure of a surface, i.e. Н is marked®0.5. Character of change of parameter Н specifies that the microstructure of a surface received by turning has irregular character, i.e. there is a tendency to its increase on a course of processing. It hypothetically corresponds, for example, to functions Е (x), Е1 (x) and Е2 (x) (fig.1) and insufficient rigidity of system can indirectly specify display of such technology factors, as deterioration of the tool, the vibrations.

Fig.3 Typical dependences of Hurst ’s parameter of a microstructure of a surface on submission and speed of cutting during turning.

On Fig.4 typical dependences of Hurst ’s parameter of a microstructure of a surface on arithmetic-mean value of height of roughnesses are presented.

.

Fig.4 Typical dependences of Hurst ’s parameter of a microstructure of a surface on arithmetic-mean value of height of roughnesses (H _(s) – Hurst 's parameter from influence of submission, H _(v) – Hurst 's parameter from influence of speed of cutting)

 

But, as it was specified above, functions log [R/S (t)] on which Hurst 's parameter is defined, have the characteristic sites specifying both on periodicity, and on accident of a microstructure of a surface (fig.5).

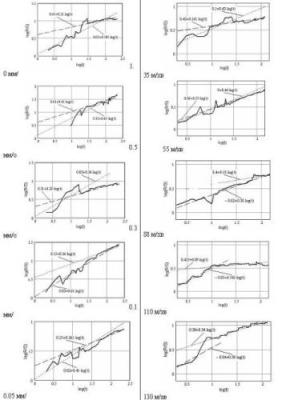
Fig. 5 Schedules of functions log [R/S (t)] for Talyrond traces received on various modes of processing at turning steel 45

On fig. 5 schedules log [R/S (t)], constructed for Talyrond traces the surfaces processed on various modes at turning are presented. Apparently from figure all functions have two characteristic sites, displaying, as «noisy», and periodic components of a microstructure of a surface. The angular factor of approximating straight lines specifies Hurst 's parameter. Analyzing schedules fig.5 it is possible to note, that at increase in submission the periodic component of a microstructure of a surface prevails, and at increase in speed of cutting – noisy.

Research of "scalability" of a microstructure of a surface which can be estimated through dependence of height of a structure (Ra) from quantity of "ledges-hollows" ₍N_L) on the fixed length of Talyrond trace is of interest. On the basis of experimental researches schedules of such dependences in double logarithmic coordinates (рис.6), approximated are received by straight lines. The received dependences are typical fractal, i.e. scale invariancy of a microstructure is shown - with increase in height of roughnesses the quantity of "ledges-hollows" decreases.

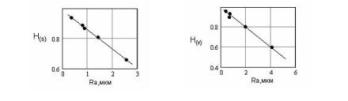
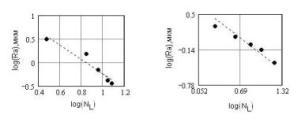
Fig. 6 Dependence of arithmetic-mean value of height of roughnesses (Ra) from quantity of "ledges-hollows" (NL) on the fixed length of Talyrond trace at change of speed of cutting a() and sizes of submission (b) at turning steel 45. Corresponding fractal dimensions »1.62 and »1.92.

 

On fig. 7 dependences log _(NL/Ra) from the logarithm of sizes of speed of cutting (a) and submissions (б) are shown.

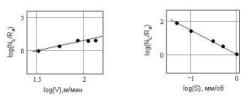
Fig. 7 Dependences log(NL/Ra)  on the logarithm of size of speed of cutting (a) and submissions (b).

Corresponding fractals dimensions »1.74 и »1.38.

 

On fig. 8 dependences log (S) and log (V) from the logarithm of arithmetic-mean value of height of roughnesses are presented. As show figures of 7 and 8 values of data in logarithmic scales settle down practically on one straight line which says about their fractal nature.

.

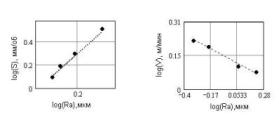
Fig. 8. Dependences log (S) and log (V) from log (Ra) at turning processing steel 45. Corresponding fractal dimensions  »1.89 и »1.28.

 

Thus, display of fractal properties of a microrelief of a surface says about self-similarity of a microrelief. And self-similarity is shown not only concerning geometrical scaling, but also concerning modes of processing. Obviously, observable self-similarity is reached by recurrence of the mechanism of the previous technological influence on a surface, but in other "scale". In that case it is necessary to find out this mechanism of "repeatability", that, most likely, it is possible only from positions of synergetrics and fractal materiology [6,7]. Besides it is possible to assume, that fractal properties of a superficial layer display processes of its self-organizing from the point of view of hierarchy of fractal structures. Revealing of such hierarchies will allow predicting and operating quality of a superficial layer of details of machines.

Conclusions

On the basis of the accomplished researches it is established:

1)      fractal properties of a microrelief of the processed surfaces depend on conditions of processing of a surface;

2)      The R/S-analysis of Talyrond trace of surfaces allows to estimate character of a microrelief from the point of view of periodicity (regularity) and «noisiness», and also to define fractal dimension;

3)      the microrelief of a surface (arithmetic-mean value, Ra) is self-similar or scale-invariant concerning modes of processing (it is shown on an example of turning);

4)      functional dependence between parameter of roughness Ra and modes of processing is unequivocally defined through fractal dimension.

 

The literature

1. Качество машин: Справочник. В 2 т. Т.1 / А.Г. Суслов, Э.Д. Браун, Н.А. Виткевич и др. – М.: Машиностроение, 1995. – 256 с.

2. А.А. Потапов, В.В. Булавкин, В.А. Герман и др. Исследование микрорельефа обработанных поверхностей с помощью методов фрактальных сигнатур. // Журнал технической физики, 2005, том 75, вып. 5. – С. 28-45.

 3. Федер Е. Фракталы. Пер. с англ. – М.: Мир, 1991. – 254 с.

4. Божокин С.В., Паршин Д.А. Фракталы и мультифракталы. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. – 128 с.

 5. Ю.Н. Кликушин. Фрактальная шкала для измерения формы распределений вероятности // Журнал радиоэлектроники № 3, 2000. – С. 15-18.

 6. Хакен Г. Синергетика. - М.: Мир, 1980. – 400с.

 

 7.  Иванова В.С., Баланкин А.С., Бунин И.Ж. и др. Синергетика и  фракталы в  материаловедении. - М.: Наука, 1994. – 383 с.