ФРАКТАЛЬНІ ВЛАСТИВОСТІ МІКРОГЕОМЕТРІЇ ОБРОБЛЕНИХ ПОВЕРХОНЬ

Науковий  керівник :: доцент, к.т.н. Матвієнко Андрій Васильович

 

Як відоме, створення поверхонь із певними мікрогеометричними властивостями є однією з основних завдань машинобудування. Особливо це ставиться до поверхонь особливо відповідальних виробів авіа-космічної техніки, приладобудування, прецизійного верстатобудування й т.д. Більше того, питання забезпечення мікрогеометрії поверхні особливо актуальне при освоєнні нових технологій обробки поверхонь як механічними, так і фізико-хімічними способами обробки, в області мікро- і нанотехнологій.

Якість поверхні традиційно характеризуються шорсткістю - среднеарифметическим відхиленням, максимальною висотою нерівностей, середнім кроком нерівностей профілю й т.п. і фізико-механічними властивостями поверхневого шару [1]. Шорсткість поверхні, як показали багато дослідників, є одним з основних показників якості поверхні. У багатьох випадках саме мікрогеометрія поверхневого шару визначає поводження поверхні в процесі її експлуатації, а у випадку мікро- і нанотехнологій шорсткість розглядається не як вторинна структура, а як властивість самої структури матеріалу.

Як правило, мікрогеометрія поверхневого шару розглядається як якийсь статичний об'єкт, що сформувався в процесі деякого впливу. Класично, в обробці матеріалів різанням, шорсткість є геометричним прообразом траєкторії переміщення інструмента, що задається кінематикою й режимами обробки. З іншої сторони в процесі обробки формуються силові, температурні й ін. поля, відбувається хімічний вплив на поверхню, виникають високі тиски в зоні контакту інструмента й оброблюваної поверхні, рух дислокацій і т.д., внаслідок чого змінюється структура поверхневого шару. Тому формування поверхні в цілому, і мікрогеометрії зокрема, є результатом дії сукупності процесів, а не тільки чисто геометричних «відгуків» дії інструмента, як, наприклад, відзначається в роботі [2 ].

У рамках розглянутої концепції «колективного» формування шорсткості можна сказати, що такий об'єкт, як мікрогеометрія поверхні є динамічною системою. Вивчення динамічної системи припускає вивчення її властивостей, які визначаються деякими інваріантами (наприклад, показник Ляпунова, ентропія й т.д.). Тому в цьому випадку використання класичних геометричних параметрів шорсткості є недостатнім або просто неможливим. Більше того, геометричні параметри не відображають таку важливу властивість шорсткості як динамічної системи - еволюцію.

Таким чином, необхідні нові підходи в оцінці мікрогеометрії поверхні й одним з таких підходів може бути використання теорії фракталов. Застосування теорії фракталов дозволить внести новий показник для оцінки шорсткості, створити базу не тільки для фрактальной класифікації, але прогнозування зміни мікрогеометрії в процесі її формування, як на стадії обробки технологічними методами, так і на стадії експлуатації. Метою даної роботи - є перевірка висунутих припущень із позицій теорії фракталов на прикладі формування мікрогеометрії поверхні на етапі технологічних впливів.

Короткі положення теорії фракталов

Загалом, фрактал - геометричний об'єкт (лінія, поверхня, просторове тіло) характеризующийся нерегулярністю (структури, геометрії й т.п.), але самоподобою (або симетрією[3,4]. Самоподоба означає, що об'єкт більш-менш одноманітно влаштований на різних масштабах його розгляду. Наприклад, на малюнках показане утворення фрактальних об'єктів методом ітерацій.

             

                         

  http://www.cs.wisc.edu/~ergreen/honors_thesis/examples.html

 Тобто, передбачається незмінність основних геометричних особливостей об'єкта при зміні масштабу. Природно існують границі цих масштабів пов'язані з поняттям кінцевої «маси» об'єкта. Нерегулярність об'єкта, загалом, означає деяку його дробову (фрактальную) розмірність, що відрізняє його від розмірності лінії, поверхні або простори. Тому в теорії фракталов використають поняття топологічної розмірності й, т.зв., розмірність Хаусдорфа-Безиковича, що і характеризує «відхилення» фрактала (об'єкта) від ідеальної топології. Таким чином, фрактали можна розглядати як безліч крапок, вкладених у простір.

Фрактальна геометрія ґрунтується на експериментальному факті, що в загальному випадку довжина L довільній кривій (яка може бути зламана в будь-якій крапці) статечним образом залежить від масштабу виміру δ:

                                                               L = C⋅δ^1-D,

де З - розмірний множник, свій для кожній кривій, D - фрактальна розмірність.

Іншою характеристикою фракталів є кореляційна розмірність. Кореляційна розмірність D2 визначається співвідношенням [26,28]:

де pi2 - імовірність того, що навмання взята крапка належить i-й осередку (кубика).

- мінімальне число n-мірних кубиків з ребром e, необхідних для покриття геометричного об'єкта.

Кореляційну розмірність можна представити у вигляді [4 ]:

                                             

де I(e) – парний кореляційний інтеграл, обумовлений з вираження:

                                ,

де ((х) - функція Хевисайда;

rn, rm – радіуси-вектори пари крапок n і m відповідно.

Парний кореляційний інтеграл визначає ймовірність того, що дві навмання взяті крапки розділені відстанню меншою, чим e. Крім того,

 

                                               ,

т. е. фрактальна розмірність D2 визначає залежність парного кореляційного інтеграла від e. Таким чином, розмірність D2 визначається значенням кореляційного інтеграла, що характеризує відносне число пари крапок (n,m), вилучених на відстані меншої e. Наступною характеристикою фрактальних властивостей об'єкта є кореляційна ентропія або інформаційна розмірність, що тією чи іншою мірою враховує частоту влучення крапки безлічі в елемент розбивки об'єкта. Числове значення ентропії є кількісною характеристикою ступеня хаотичності системи.

Корреляционна ентропія D1 визначається з наступного вираження [4 ]:

                                  ,

де S(ε ) - ентропія фрактальної безлічі,

Pi  - імовірність знаходження крапки об'єкта в i-й осередку розбивки об'єкта.

Кореляційна ентропія може бути обчислена через кореляційний інтеграл.

            Як правило, визначення кореляційної розмірності й ентропії здійснюється для мультифракталів – неоднорідних фрактальних об'єктів, які мають не тільки геометричні, але й статистичні характеристики. Іншими словами неоднорідні фрактали мають нерівномірний розподіл крапок безлічі або різну щільність «заселеності» безлічі. Тому, при дослідженні мультифракталів говорять про узагальнення фрактальної розмірності [3,4], яка може бути представлена вищепредставленими фрактальними розмірностями. Але у зв'язку з особливою специфікою мультифракталів для аналізу використають функцію  мультифрактального спектра або спектр сингулярностей мультифрактала. Як відзначено в роботі [4], величина функції мультифрактального спектра фактично дорівнює хаусдорфовой розмірності (D) деякого однорідного фрактального підмноження з вихідної безлічі, що дає домінуючий внесок у статистичні характеристики безлічі. Тому в першому наближенні можна вважати, що D є фрактальною розмірністю щодо однорідних фракталов у мультифрактальній безлічі.

Таким чином, до основних характеристик фрактала ставиться його розмірність: узагальнена або хаусдорфова D, кореляційна D2 і інформаційна D1.

Показник Херста

Існують різні способи визначення фрактальних розмірностей, до числа яких ставиться т.зв. R/S-спосіб, на підставі, якого визначається показник Херста [3]. Цей показник має широке застосування в аналізі тимчасових рядів завдяки своїй чудовій стійкості. Він містить мінімальні припущення про досліджувану систему й може класифікувати тимчасові ряди. Він може відрізнити випадковий ряд від невипадкового, навіть якщо випадковий ряд не гауссовский (тобто не нормально розподілений).

Для порівняння різних типів тимчасових рядів Херст увів наступне співвідношення:

                                                       R/S=(a·N)Н,

де R/S – нормований розмах від накопиченого середнього, N – число спостережень, а – деяка константа, Н – показник Херста.

Є три різних класифікації для показника Херста:

1) Н = 0.5. Указує на випадковий ряд. Події випадкові й некоррелірованні. Сьогодення не впливає на майбутнє. Функція щільності ймовірності може бути нормальною кривою, однак це не обов'язкова умова. R/S-аналіз може класифікувати довільний ряд, безвідносно до того, який вид розподілу йому відповідає.

2) 0 ≤ Н< 0.5. Даний діапазон відповідає антиперсистентним, або эргодичним рядам. Такий тип системи часто називають – «поверненням до середнього». Якщо система демонструє «ріст» у попередній період, то, швидше за все, у наступному періоді почнеться спад. І навпаки, якщо йшло зниження, то ймовірний близький підйом. Стійкість такого антиперсистентного поводження залежить від того, наскільки Н близько до нуля. Такий ряд більше мінливий, чим ряд випадковий, тому що складається із частих реверсів спад-підйом.

3) 0.5 < Н < 1.0. Маємо персистентні, або трендостійкі ряди. Якщо ряд зростає (убуває) у попередній період, то імовірно, що він буде зберігати цю тенденцію якийсь час у майбутньому. Чим ближче Н к 0.5, тим більше зашумлен ряд і тем менш виражений його тренд. Персистентий ряд – це узагальнення броуновского руху, або зміщені випадкові блукання. Сила цього зсуву залежить від того, наскільки Н більше 0.5.

Існує ще й четверта характеристика показника Херста, коли Н>1. У цьому випадку говорять про статистику Леви й про процес (або тимчасовий ряд) із фрактальним часом, про тимчасові крапки розриву похідній. Це означає, що відбуваються незалежні перегони амплітуди, розподілені по Леви за час, певний величиною стрибка, і зростаючи разом з ним. Дисперсія збільшення за даний інтервал часу стає кінцевою, траєкторія у фазовому просторі зберігає свій вид, але з'являється новий фрактальний об'єкт - тимчасові крапки розриву похідній.

Якщо в подвійних логарифмічних координатах знайти нахил R/S як функцію від N, то тим самим одержимо оцінку Н. Ця оцінка не пов'язана з якими-небудь припущеннями щодо лежачої в основі розподілу, хоча в роботі [ ] почата спроба класифікації випадкових розподілів на основі фрактальної шкали[5].

Для дуже великої кількості спостережень N можна чекати збіжності ряду до величини Н=0.5, тому що ефект пам'яті зменшується до того рівня, коли стає непомітним. Інакше кажучи, у випадку довгого ряду спостережень можна чекати, що його властивості стануть невідрізненими від властивостей звичайного броуновского руху, або простого випадкового блукання, оскільки ефект пам'яті розсіюється.

Показник Херста може бути перетворений у фрактальну розмірність D за допомогою наступної формули [3-5 ]:   

D=2-H

Фрактальна розмірність тимчасового ряду, або накопичених змін при випадковому блуканні, дорівнює 1.5. Фрактальна розмірність кривої лінії дорівнює 1, а фрактальна розмірність геометричної площини дорівнює 2. Таким чином, фрактальна розмірність випадкового блукання лежить між кривою лінією й площиною. Якщо Н = 0.5, то D = 1.5. Обидві величини характеризують незалежну випадкову систему. Величина 0.5 < Н ? 1 буде відповідати фрактальної розмірності, більше близької до кривої лінії. Це персистентний часовий ряд, що дає більше гладку, менш зазубрену лінію, ніж випадкове блукання. Антиперсистентна величина Н (0 < Н < 0.5) дає відповідно більше високу фрактальну розмірність і більше переривчасту лінію, чим випадкове блукання, і, отже, характеризує систему, більше піддану змінам.

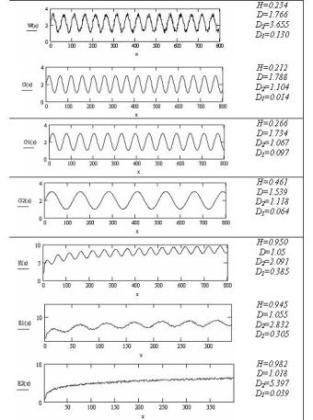
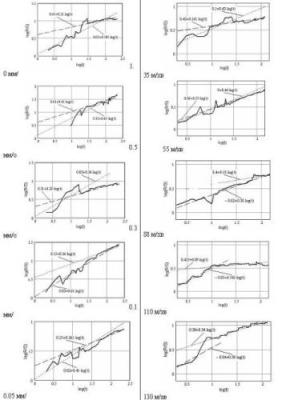
Для приклада на мал. 1 представлені графіки різних функцій з показником Херста (H), фрактальною розмірністю (D), кореляційною розмірністю (D2) і кореляційною ентропією (D1).

З наведених фрактальних характеристик легко можна простежити за їхньою зміною по зміні форми графіків функцій. Так, більше «зашумлені» функції по своїм фрактальним характеристикам відрізняються від ідеальних. Наприклад, функції W(x) і G(x), які описуються однаковими вираженнями, але в W(x) додан шумовий компонент, рівномірно розподілений на інтервалі [0-0.5]. Якщо розглянути, наприклад, синусоїдальні функції G(x), G1(x) і G2(x) то можна помітити, що зі збільшенням періоду функції показник Херста наближається до Н=0.5. Це говорить про «наближення» функції до прямій, тобто синусоїда «витягається» у пряму.

 

 

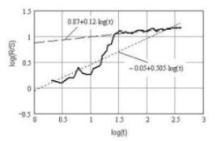
Мал.1. Фрактальні характеристики функцій

 

Функції Е(х), Е1(х) і Е2(х) типові представники персистентних рядів. Шум в Е2(х) незначний у порівнянні із загальною трендостійкістю, тому показник Н більше, ніж для функцій Е(х) і Е1(х), де явно виражені не тільки т трендостійкістю, але й періодичність. Причому явно різні періоди не значно впливають на зміну показника Н у порівнянні з функціями G(x), G1(x) і G2(x). Функція А(х) являє собою випадкове блукання аргументу, що відображає показник Н близький до 0.5.

Таким чином, з наведених прикладів видний взаємозв'язок між видом функції (тимчасового ряду) і показником Херста, що говорить про можливості його використання для класифікації функцій (рядів). Тим часом, існує ще одна особливість визначення показника Херста. Як відзначалося вище для його визначення необхідно апроксимувати пряму R/S як функцію від N у подвійних логарифмічних координатах. Але при цьому, як правило, не виділяються характерні ділянки функції log[R/S(N)] і апроксимація здійснюється т.зв. «усередненням». Наприклад, для функції W(x) маємо показник Херста, що чітко вказує на періодичність (антиперсистентность), але нічого не каже про випадкову складову, що не істотна в порівнянні з явно вираженою періодичністю. Для виявлення таких характерних рис функцій (тимчасового ряду) доцільно виконувати апроксимацію не по «середньому» функції log[R/S(N)], а по характерних ділянках цієї функції. Наприклад, на мал. 2 представлений графік функції log[R/S(N)] (на малюнку кількість 

спостережень або відліків N позначене через t), побудованої по функції W(x), де апроксимації піддаються дві характерних ділянки. 

 

 

Мал.2. Графік функції log[R/S(t)] для W(x) і його апроксимації

 

Як видно з малюнка дві характерних ділянки добре апроксимуються відповідними прямими, які вказують на показники Херста 0.12 і 0.505, що відповідає періодичності й зашумленості функції W(x).

Фрактальна характеристика мікрогеометрії поверхневого шару

Для вивчення фрактальних характеристик мікрогеометрії поверхневого шару були використані профілограми, отримані після різних видів механічного впливу на оброблювану поверхню сталевих заготівель. Фрактальна розмірність профилограм оцінювалася по наведеним вище характеристикам: показник Херста, кореляційна розмірність і кореляційна ентропія. Показник Херста визначався як по «усередненню» всіх аргументів (довжини профілограми), так і по характерних ділянках функції log[R/S(t)].

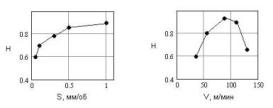
Більше детальним дослідженням піддавалися профілограми, отримані після обробки гострінням на різних режимах подачі й швидкості різання.

На мал. 3 представлені графіки залежностей показника Херста мікропрофілю поверхні, розрахованого по «усередненню» функції log[R/S(t)], від подачі й швидкості різання. Як видно з малюнка, показник Н перебуває в діапазоні 0.5... 1, що вказує на персистентність профилограм. На деяких режимах обробки відзначається випадкове блукання мікропрофілю поверхні, тобто Н®0.5. Характер зміни показника Н указує на те, що мікропрофіль поверхні, отриманий гострінням носить нерегулярний характер, тобто є тенденція до його збільшення по ходу обробки. Це гіпотетично відповідає, наприклад, функціям Е(х), Е1(х) і Е2(х) (мал. 1) і може побічно вказувати на прояв таких технологічних факторів, як зношування інструмента, вібрації, недостатня твердісті системи.

Мал.3 Типові залежності показника Херста мікропрофілю поверхні від подачі й швидкості різання при гострінні.

На мал. 4 представлені типові залежності показника Херста мікропрофілю поверхні від середнєарифметичного значення висоти нерівностей

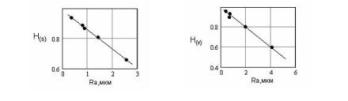
Мал.4 Типові залежності показника Херста мікропрофілю поверхні від середнеарифметичного значення висоти нерівностей (H(s) – показник Херста від впливу подачі , H(v) – показник Херста від впливу швидкості різання)

 

Але, як вказувалося вище, функції log[R/S(t)], по яких визначається показник Херста, мають характерні ділянки, що вказують як на періодичність, так і на випадковість мікропрофілю поверхні (мал. 5).

Мал. 5 Графіки функцій log[R/S(t)] для профилограм, отриманих на різних режимах обробки при гострінні стали 45

На мал. 5 представлені графіки log[R/S(t)], побудовані для профилограм поверхонь, оброблених на різних режимах при гострінні. Як видно з малюнка всі функції мають дві характерних ділянки, що відображають, як «шумову», так і періодичну складового мікропрофілю поверхні. Кутовий коефіцієнт апроксимуючих прямих указує на показник Херста. 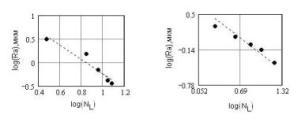Аналізуючи графіки мал.5 можна відзначити, що при збільшенні подачі превалює періодична складова мікропрофілю поверхні, а при збільшенні швидкості різання - шумова.

Становить інтерес дослідження «масштабованості» мікропрофілю поверхні, що може бути оцінений через залежність висоти профілю (Ra) від кількості «виступів-западин» (NL) на фіксуваній довжині профілограми. На підставі експериментальних досліджень отримані графіки таких залежностей у подвійних логарифмічних координатах (мал.6), аппроксимірованими прямими. Отримані залежності є типовими фрактальними, тобто проявляється масштабна інваріантість мікропрофілю - зі збільшенням висоти нерівностей зменшується кількість «виступів-западин». 

 

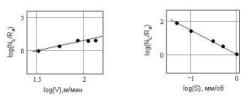
Мал. 6 Залежність середнєарифметичного значення висоти нерівностей (Ra) від кількості «виступів-западин» (NL) на фіксуємої довжині профілограми при зміні швидкості різання (а) і величини подачі (б) при гострінні стали 45. Відповідні фрактальні розмірності  »1.62 и »1.92.

 

На мал. 7 показані залежності log(NL/Ra) від логарифма величин швидкості різання (а) і подачі (б).

 

Мал. 7 Залежності log(NL/Ra)   від логарифма величини швидкості різання (а) і подачі (б). Corresponding fractal dimensions  »1.74 и »1.38.

  На мал. 8 представлені залежності log(S) і log(V) від логарифма середнєарифметичного значення висоти нерівностей. Як показують малюнки 7 і 8 значення даних у логарифмічних масштабах розташовуються практично на одній прямій, що говорить про їх фрактальну природу.

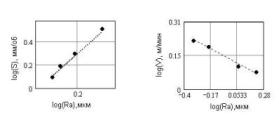
Рис. 8. Зависимости log(S) и log(V) от log(Ra) при токарной обработке стали 45. Соответствующие фрактальные размерности »1.89 и »1.28.

иерархия

Таким чином, прояв фрактальних властивостей мікрорельєфу поверхні говорить про самоподобу мікрорельєфу. Причому самоподоба проявляється не тільки щодо геометричного масштабування, але й щодо режимів обробки. Очевидно, спостережування самоподоби досягається шляхом повторення механізму попереднього технологічного впливу на поверхню, але в іншому «масштабі». У такому випадку необхідно з'ясувати цей механізм «повторюваності», що, швидше за все, можливо тільки з позицій синергетики й фрактального матеріалознавства [6,7]. Крім того, можна припустити, що фрактальні властивості поверхневого шару відображають процеси його самоорганізації з погляду ієрархичності фрактальних структур. Виявлення такого роду ієрархій дозволить прогнозувати й управляти якістю поверхневого шару деталей машин.

Висновки

На підставі виконаних досліджень установлено:

1) фрактальні властивості мікрорельєфу оброблених поверхонь залежать від умов обробки   поверхні;

 2) R/S-аналіз профілограм поверхонь дозволяє оцінити характер мікрорельєфу з погляду періодичності (регулярності) і «зашумленості», а також визначити фрактальну розмірність;

 3) мікрорельєф поверхні (середнєарифметичне значення, Ra) є самоподібним або           масштабно-інваріантним щодо режимів обробки (показано на прикладі гостріння);

4) функціональна залежність між параметром шорсткості Ra і режимами обробки однозначно визначається через фрактальну розмірність.

 

Література . 1. Качество машин: Справочник. В 2 т. Т.1 / А.Г. Суслов, Э.Д. Браун, Н.А. Виткевич и др. – М.: Машиностроение, 1995. – 256 с.

2. А.А. Потапов, В.В. Булавкин, В.А. Герман и др. Исследование микрорельефа обработанных поверхностей с помощью методов фрактальных сигнатур. // Журнал технической физики, 2005, том 75, вып. 5. – С. 28-45.

3. Федер Е. Фракталы. Пер. с англ. – М.: Мир, 1991. – 254 с.

 4. Божокин С.В., Паршин Д.А. Фракталы и мультифракталы. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. – 128 с.

 5. Ю.Н. Кликушин. Фрактальная шкала для измерения формы распределений вероятности // Журнал радиоэлектроники № 3, 2000. – С. 15-18.

 6. Хакен Г. Синергетика. - М.: Мир, 1980. – 400с.

7. Иванова В.С., Баланкин А.С., Бунин И.Ж. и др. Синергетика и фракталы в материаловедении. - М.: Наука, 1994. – 383 с.