Цели и задачи
Цель работы состоит в разработке эффективного параллельного алгоритма построения аналитической модели кластерной системы, что позволит повысить эффективность функционирования кластерных систем на основе использования полученных результатов.
Задачи исследования:
- разработка Марковских моделей функционирования кластерных систем;
- разработка параллельных алгоритмов реализации для задач большой размерности;
- построение эффективного параллельного алгоритма решения СЛАУ большой размерности с разреженной матрицей общего вида;
- усовершенствование существующих методов расчета основных характеристик функционирования кластерных систем.
Актуальность темы
Анализ способов построения высокопроизводительных кластерных систем и средств оценки их эффективности показывает сложность решения задачи анализа и синтеза этих вычислительных систем. Традиционных, классических решений этой задачи уже недостаточно и возникает необходимость в разработке новых подходов для её решения.
- Наличие конфликтных ситуаций при использовании общих ресурсов, а также несоответствие программ архитектуре ВС приводят к снижению производительности вычислительных систем. Для оценки и рекомендации на стадии проектирования следует использовать аналитические методы анализа, а именно, аппарат марковских цепей.
- Аналитические методы, в основном, используются для анализа производительности однопроцессорных ВС, преимущественно с последовательной обработкой данных. Для ВС с параллельной обработкой данных и для многопроцессорных ВС, например, многопроцессорных структур, в том числе, кластерных, аналитические методы требуют дальнейшего развития.
- В существующих публикациях недостаточно полно описаны рекомендации использования дискретных Марковских моделей.
- Дискретные Марковские модели, описывающие проектируемые вычислительные сети, имеют большую размерность и в большинстве случаев не решаются на ЭВМ ввиду ограниченности вычислительных ресурсов.
Одним из способов решения этой проблемы является распараллеливание этих алгоритмов. Необходимо построить параллельный алгоритм, оценив параметры параллелизма.
- Большое значение для проектирования ВС имеют не только задача анализа, но и задача синтеза. Однако для современных вычислительных структур, когда в системах «клиент-сервер» количество клиентов достигает сотни, задачи синтеза не разрешаются ввиду большой размерности и нелинейности системы уравнений, получаемой при решении задачи. Нахождение способа решения таких задач позволит сократить процесс проектирования ВС большой размерности.
Научная новизна
Полученные алгоритмы можно использовать для оценки эффективности параллельных вычислительных систем на стадии проектирования, эксплуатации и модернизации.
Разработанный параллельный метод решения систем линейных алгебраических уравнений с разреженными матрицами может применяться при численном исследовании стационарных и нестационарных, линейных и нелинейных процессов в задачах математического моделирования, в том числе оптимизационных и междисциплинарных, где многократное решение СЛАУ является наиболее ресурсоемким этапом.
Обзор исследований и разработок по теме
В связи с большим количеством создаваемых параллельных вычислительных систем (ВС), работы в этом направлении требуют
дальнейшего развития, не утрачивают своей актуальности. Большой вклад в решение проблем создания новых многопроцессорных
архитектурных реализаций и оценки их эффективности внесли Лебедев С.А., Глушков В.М. , Капитонова Ю.В. , Самофалов К.Г.,
Забродин А.В. [1,2], Каляев А.В.[3], Бурцев В.С. [4], Боюн В.П.[5], Митрофанов Ю.И. [6], Бошарин Г.П. [7], Коган Я.А [7,8],
Менаске Д. и Алмейда В. , Кемени Дж., Столингс У. [9].
Множество задач, решаемых на многопроцессорных системах, требуют решения больших систем линейных уравнений с
разреженными матрицами
Ax = b,
где A — задаваемая пользователем разреженная матрица n x n,
b — задаваемый пользователем вектор длины n,
x — вектор длины n, который должен быть вычислен.
Причем, как правило, решение задач линейной алгебры занимает значительную часть (50 % и более) времени решения всей
задачи в целом [19]. Поэтому существует целый ряд инструментальных средств, призванных распараллелить решение СЛАУ.
Рассмотрим библиотеки методов, использующие стандарт MPI и имеющие стредства для решения СЛАУ с разреженными матрицами.
Обзор параллельных библиотек
Aztec [10]
Пакет подпрограмм Aztec разработан в исследовательской лаборатории параллельных вычислений Сандии (США) для решения итерационными методами систем линейных уравнений.
Aztec включает в себя процедуры, реализующие ряд итерационных методов Крылова:
- метод сопряженных градиентов (CG),
- обобщенный метод минимальных невязок (GMRES),
- квадратичный метод сопряженных градиентов (CGS),
- метод квазиминимальных невязок (TFQMR),
- метод бисопряженного градиента (BiCGSTAB) со стабилизацией.
Все методы используются совместно с различными переобуславливателями (полиномиальный метод и метод декомпозиции областей, использующий как прямой метод LU, так и неполное LU разложение в подобластях).
BlockSolve95
- Параллельная библиотека для решения разреженных систем линейных уравнений. Реализована с помощью MPI.
- Библиотека разработана в Argonne National Laboratory/MCS division. Распространяется бесплатно.
P-Sparslib
- PSPARSLIB (A Portable Library of Parallel Sparse Iterative Solvers) — библиотека параллельных итеративных решателей для разреженных линейных систем.
ScaLAPACK[11]
- Библиотека ScaLAPACK включает подмножество процедур LAPACK, переработанных для использования на MPP-компьютерах, включая: решение систем линейных уравнений, обращение матриц, ортогональные преобразования, поиск собственных значений и др.
- Библиотека ScaLAPACK разработана с использованием PBLAS (параллельные версии BLAS уровней 1,2,3) и коммуникационной библиотеки BLACS.
- Поддерживается на платформах IBM RS/6000 SP, Intel Paragon, SGI Origin 2000, и HP Exemplar, а также на кластерах рабочих станций. Может быть портирована на любую платформу, где поддерживается PVM или MPI.
- ScaLAPACK — совместный проект нескольких организаций (Oak Ridge National Laboratory, Rice University, University of California at Berkeley University of California at LA University of Illinois, University of Tennessee at Knoxville)
PETSc[12]
- Набор процедур и структур данных для параллельного решения научных задач с моделями, описываемыми в виде дифференциальных уравнений с частными производными.
- Библиотека реализована с помощью MPI.
- Поддерживаемые платформы: рабочие станции Sun, RS/6000 включая SP, SGI IRIX — 32-битные и 64-битные версии, HP Exemplar, Cray T3D/T3E, DEC Alpha, Linux/FreeBSD/Windows NT на Intel.
- Библиотека разработана в Argonne National Laboratory/MCS division. Распространяется бесплатно.
- Модуль KSP (Krylov subspace method – метод подпространств Крылова) является сердцем PETSc, поскольку он обеспечивает унифицированный и эффективный доступ ко всем средствам для решения систем линейных алгебраических уравнений (СЛАУ).
- Комбинация метода подпространств Крылова (KSP) и предобуславливателя (PC – preconditioner) находится в центре самых современных программ для решения линейных систем итерационными методами.
- Модуль KSP предоставляет многие популярные итерационные методы на основе подпространств Крылова: Conjugate Gradient, GMRES, CG-Squared, Bi-CG-stab и др.
- Модуль РС включает разнообразные предобуславливатели: Block Jacobi, Overlapping Additive Schwarz, ICC, ILU via BlockSolve95, ILU(k), LU (прямой метод, работает только на одном процессоре), Arbitrary matrix и др.
PLAPACK
- Пакет параллельных процедур линейной алгебры. Включает параллельные версии процедур решения систем линейных уравнений с помощью LU и QR-разложений, разложения Холецкого.
- Пакет PLAPACK реализован с помощью MPI. Включает интерфейсы для языков Fortran и С.
- Пакет PLAPACK разработан в университете шт. Техас (Austin). Доступен бесплатно.
- Руководство пользователя было издано в издательстве MIT Press: Robert van de Geijn, "Using PLAPACK: Parallel Linear Algebra Package" (1997).
В ДонНТУ в последние годы подобной тематикой занимались магистранты:
- Кучереносова Ольга (Руководитель:проф.Башков Е.A.)
Тема магистерской работы: «Исследование эффективности параллельных вычислительных систем»
- Мищук Юлия (Руководитель: проф. Фельдман Л.П.)
Тема магистерской работы: «Анализ эффективности вычислительных систем с использованием Марковской модели»
- Горб Павел (Руководитель:доц. Ладыженский Ю.В.)
Тема магистерской работы: «Решение больших систем линейных алгебраических уравнений в распределенной вычислительной среде»
- Аль-Масри Мохаммед Рида (Руководитель:доц. Ладыженский Ю.В.)
Тема магистерской работы: «Параллельные методы решения СЛАУ на вычислительном кластере»
Построение марковской модели однородного вычислительного кластера
Одним из примеров вычислительных систем с распределенной обработкой являются кластеры. Они обладают высокой производительностью и «живучестью» вычислительных ресурсов. Классификация кластерных систем по cовместному использованию одних и тех же дисков отдельными узлами является самой распространенной [14,15]. Одной из основных проблем при построении ВС с распределенной обработкой является выработка рекомендации для рационального использования ресурсов этой сети. Эта задача возникает как при эксплуатации, так и при проектировании сети. Для эффективной эксплуатации кластерной системы необходимо построить её аналитическую модель и для каждого класса решаемых задач определить основные параметры вычислительной среды. Эти модели можно использовать и для оптимизации ВС на стадии проектирования.
В данной работе рассматривается кластер с совместным использованием дискового пространства. Такие топологии используют СУБД Oracle Parallel Server и Informix [15]. Производительность таких систем может увеличиваться как путем наращивания числа процессоров и объемов оперативной памяти в каждом узле кластера, так и посредством увеличения количества самих узлов.
Принципиальная схема кластера такого типа приведена на рисунке 1.
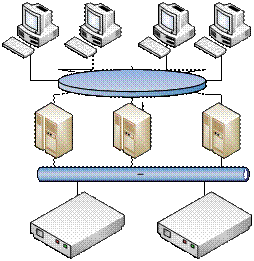 Рисунок 1 — Архитектура кластера с совместным использованием дискового пространства
Рисунок 1 — Архитектура кластера с совместным использованием дискового пространства
Упрощенная модель кластера с совместным использованием дискового пространства приведена на рис. 2
Входной узел (управляющий сервер) равномерно распределяет между серверами приложений (выполняющими одинаковые приложения) задачи. Количество серверов – приложений — N1. Каждый из них может обратиться к данным, расположенным на дисках, количество которых N2. Ввиду ограниченных вычислительных возможностей будем считать, что количество задач, обрабатываемое такой вычислительной системой не более М.
Построим дискретную Марковскую модель. Так как кластер однородный, представим серверы, и, аналогично, дисковые накопители многоканальными устройствами. Требования, поступающие на обслуживание на серверы, поступают в ограниченную очередь (не более М), из которой на обслуживание выбираются по правилу «первый пришел – первый обслужился».
Допустим, задачи, обрабатываемые на таком кластере, однородные и имеют следующие характеристики:
p12 – вероятность запроса к одному из N1 серверов,
p23 — вероятность запроса к одному из N2 дисков,
p21 – вероятность завершения обслуживания одним из N1 серверов,
p10 – вероятность завершения обслуживания задачи,
q0 – вероятность появления новой задачи.
 Рисунок 2 — Структурная схема Марковской модели кластера с совместным использованием дискового пространства
Рисунок 2 — Структурная схема Марковской модели кластера с совместным использованием дискового пространства
(анимация: объем — 47 КБ, количество кадров — 12, количество циклов повторения — 5, размер — 702x136)
При построении модели используется методика, предложенная в [16].
Алгоритм построения дискретной Марковской модели состоит из двух частей: вычислений матрицы переходных вероятностей и вектора стационарных вероятностей.
При определении матрицы переходных вероятностей используются следующие параметры:
N — количество узлов в моделируемой системе (устройств или их блоков)
M – количество заявок в системе.
Число состояний системы равно числу размещений j задач по N узлам и определяется по формуле:
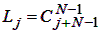 ,
общее количество состояний вычисляется так:
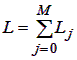 .
Общее количество ненулевых элементов матрицы переходных вероятностей вычисляется как:
В таблице приведены результаты расчетов доли ненулевых элементов в матрице переходных вероятностей для модели
с тремя группами устройств N=3 [17].
| Количество задач М |
| 20 |
50 |
100 |
200 |
| Размерность матрицы переходных вероятностей (количество состояний модели) |
| 1771 x 1771 |
23426 x 23426 |
176851 x 176851 |
1373701 x 1373701 |
| Количество ненулевых элементов |
| 1257408 |
94113953 |
2746496028 |
83871314553 |
| Доля ненулевых элементов в матрице переходных вероятностей |
| 0.4009 |
0.1715 |
0.0878 |
0.0444 |
Размерность получаемых матриц зависит от количества задач в моделируемой системе.
Порядок возникающих матриц – от десятков и сотен тысяч до десятков миллионов. Это вызвано желанием оперировать более точными дискретными моделями, позволяющими получать приближенные решения, более близкие к решениям исходных задач, лучше учитывать локальные особенности рассматриваемого процесса.
Решение таких задач требует значительных вычислительных ресурсов, которые могут быть представлены параллельными компьютерами. Поэтому является актуальной проблема создания параллельных алгоритмов решения данной задачи.
Важной особенностью получаемых матриц является тот факт, что сумма элементов по каждой строке равна единице,
независимо от их числа. Отсюда вытекает еще одна сложность обработки таких матриц: порядок элементов в матрице может сильно
разниться – от 0,5 до 10-17. То есть к подобным матрицам нельзя применить масштабирование без потерь точности.
Следующей особенностью получаемых матриц является то, что они общего вида, т.е. не могут просто быть преобразованы к одному из стандартных видов: симметричному, ленточному, блочно-диагональному с окаймлением и т.п., для которых уже разработаны эффективные параллельные алгоритмы [18-21]
Итак, к разрабатываемому алгоритму решения СЛАУ на таких разреженных матрицах выдвигается ряд требований:
- схема хранения матрицы должна быть особой: хранятся только ненулевые элементы и информация об их расположении в исходной матрице[22];
- метод решения СЛАУ предотвращать потерю точности при вычислениях
- параллельный алгоритм должен быть эффективным и масштабируемым.
Ожидаемые результаты
- разработать дискретную модель кластера, с помощью которой можно получить основные характеристики вычислительной среды;
- разработать новый параллельный алгоритм реализации дискретной Марковской модели однородного кластера;
- получить основные характеристики распараллеливания;
- разработать параллельный алгоритм решения СЛАУ большой размерности с разреженными матрицами общего вида.
Важное замечание
При написании данного автореферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2010г.
Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список ссылок
- Забродин А.В., Левин В.К. Опыт разработки параллельных вычислительных технологий, создание и развитие семейства МВС.
// Тезисы докладов конференции «Высокопроизводительные вычисления и их приложения». 30 октября-2 ноября 2000 года, Черноголовка.
— М.:МГУ, 2000. — с. 20-21.
- Забродин А.В. Параллельные вычислительные технологии. Состояние и перспективы // Материалы первой молодежной школы
«Высокопроизводительные вычисления и их приложения».
- Каляев А. В., Левин И.И. Модульно-наращиваемые многопроцессорные системы со структурно-процедурной организацией вычислений. —
М.: Янус-К, 2003. — 380 с.
- Бурцев В.С. СуперЭВМ в России. История и перспективы. — ЭЛЕКТРОНИКА: НТБ, 2000, №4, с. 5–9.
- Малиновский Б. Н., Боюн В.П., Козлов Л. Г. Введение в кибернетическую технику. Параллельные структуры и методы.
— Киев: Наук. думка, 1989. — 245 с.
- Митрофанов Ю.И. Основы теории сетей массового обслуживания. — Саратов: Изд-во Сарат.ун-та, 1993. — 116 с.
- Бошарин Г.П., Бочаров П.П., Коган Я.А. Анализ очередей в вычислительных сетях. Теория и методы расчета. — М.: Наука, 1989.— 336 с.
- Авен О.И., Гурин Н.Н., Коган Я.А. Оценка качества и оптимизация вычислительных систем. — М.: Наука,1982. — 464 с.
- Столингс У. Структурная организация и архитектура компьютерных систем. — М.: Вильямс, 2002. — 893 с.
- Аztec — a massively parallel iterative solver library for solving sparce linear systems [Электронный ресурс]
/ Интернет-ресурс. — Режим доступа: http://www.cs.sandia.gov/CRF/aztec1.html
- ScaLAPACK Home Page [Электронный ресурс] / Интернет-ресурс. — Режим доступа: http://www.netlib.org/scalapack/scalapack_home.html
- PETSc — Portable, Extensible Toolkit for Scientific Computation [Электронный ресурс] / Интернет-ресурс. —
Режим доступа: http://www.mcs.anl.gov/petsc/petsc-as/
- METIS — Family of Multilevel Partitioning Algorithms [Электронный ресурс] / Интернет-ресурс. —
Режим доступа: http://glaros.dtc.umn.edu/gkhome/views/metis/
- Спортак М., Франк Ч., Паппас Ч. и др. Высокопроизводительные сети. Энциклопедия пользователя. — К.: ДиаСофт, 1998. — 432 с.
- Цилькер Б.Я., Орлов С.А. Организация ЭВМ и систем. — М: ПИТЕР, 2004. — 668 с.
- Фельдман Л.П., Малинская Э.Б. Аналитическое моделирование вычислительных систем с приоритетным обслуживанием программ.
//Электронное моделирование. — К., 1985. — №6.— с. 78-82.
- Дяченко Т.Ф., Михайлова Т.В. Методы решения больших СЛАУ на разреженных матрицах общего вида // Тезизы доклада на IV международной
научно-практической конференции молодых ученых, аспирантов,студентов «Современная информационная Украина: Информатика, Экономика, Философия»,
13-14 мая 2010г., Государственный Университет информатики и искусственного интеллекта, Донецк
- Попов А.В. Параллельные алгоритмы решения линейных систем с разреженными симметричными матрицами.
// Штучний інтелект. — Д.,2006. — №4. — с. 248-257.
- Химич А.Н., Попов А.В., Т.В. Чистякова, О.В. Рудич, Т.А. Герасимова. Исследование блочно-циклических алгоритмов на семействе кластеров СКИТ.
// Проблеми програмування. — К., 2006. — № 2-3. — с. 177-183.
- Игнатьев А.В., Ромашкин В.Н.. Анализ эффективности методов решения больших разреженных систем линейных алгебраических уравнений.
// Интернет-вестник ВолгГАСУ. Сер.: Строит. информатика. 2008. — №3(6). — с. 1-7.
- Ильин В.П. Проблемы высокопроизводительных технологий решения больших разреженных СЛАУ.
// Вычислительные методы и программирование. — М., 2009. — №10. — с. 141-147.
- Тьюарсон Р. Разреженные матрицы. Пер. с англ. М: Мир, 1977. — 189 с.
|





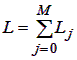 .
.