Дяченко Тетяна Федорівна

Тема випускної роботи:«Дослідження паралельного алгоритму побудови Марковських моделей обчислювальних систем»

Керівник: к.фіз-мат.н., доцент Дацун Н. М.

Консультант: к.т.н., доцент Михайлова Т. В.

Автореферат за темою магістерської роботи

Дослідження паралельного алгоритму

побудови Марковських моделей

обчислювальних систем

Мета і завдання

Мета роботи полягає у розробці ефективного паралельного алгоритму побудови аналітичної моделі кластерної системи, що дозволить підвищити ефективність функціонування кластерних систем.

Завдання дослідження:

• розробити Марковську модель функціонування кластерних систем;
  
  
• розробити паралельні алгоритми реалізації задач великої розмірності;
  
  
• побудувати ефективний паралельний алгоритм розв'язання СЛАР великої розмірності з розрідженою матрицею загального вигляду;
  
  
• удосконалити існуючі методи розрахунку основних характеристик функціонування кластерних систем.

Актуальність теми

Аналіз способів побудови високопродуктивних кластерних систем і засобів оцінки їх ефективності показує складність рішення задачі аналізу та синтезу цих обчислювальних систем. Традиційних, класичних рішень цього завдання вже недостатньо і виникає необхідність у розробці нових підходів для її вирішення.

1. Наявність конфліктних ситуацій при використанні загальних ресурсів, а також невідповідність програм архітектурі обчислювальних систем (ОС) призводять до зниження продуктивності обчислювальних систем. Для оцінки і рекомендації на стадії проектування слід використовувати аналітичні методи аналізу, а саме, апарат марковських ланцюгів.
   
   
2. Аналітичні методи, здебільшого, використовуються для аналізу продуктивності однопроцесорних обчислювальних систем, переважно з послідовною обробкою даних. Для обчислювальних систем з паралельною обробкою даних і для багатопроцесорних обчислювальних систем, наприклад, багатопроцесорних структур, в тому числі, кластерних, аналітичні методи вимагають подальшого розвитку.
   
   
3. В наявних публікаціях недостатньо повно описані рекомендації використання дискретних Марковських моделей.
   
   
4. Дискретні Марковські моделі, які описують спроектовані обчислювальні мережі, мають велику розмірність і в більшості випадків не вирішуються на ЕОМ через обмеженість обчислювальних ресурсів. Одним із способів вирішення цієї проблеми є розпаралелювання цих алгоритмів. Необхідно побудувати паралельний алгоритм, оцінивши параметри паралелізму.
   
   
5. Велике значення для проектування обчислювальних систем мають не тільки завдання аналізу, але і завдання синтезу. Однак для сучасних обчислювальних структур, коли в системах «клієнт-сервер» кількість клієнтів сягає сотні, завдання синтезу не вирішуються через велику розмірності й нелінійності системи рівнянь, що виникають при вирішенні задачі. Знаходження способу вирішення таких завдань дозволить скоротити процес проектування обчислювальних систем великої розмірності.

Наукова новизна

Отримані алгоритми можна використовувати для оцінки ефективності паралельних обчислювальних систем на стадії проектування, експлуатації та модернізації.

Розроблений паралельний метод розв'язання систем лінійних алгебраїчних рівнянь з розрідженими матрицями може застосовуватися при чисельному дослідженні стаціонарних і нестаціонарних, лінійних та нелінійних процесів у задачах математичного моделювання, у тому числі оптимізаційних і міждисциплінарних, де багаторазове рішення СЛАР є найбільш ресурсоємним етапом.

Огляд досліджень і розробок по темі

У зв'язку з великою кількістю створюваних паралельних обчислювальних систем роботи в цьому напрямку потребують подальшого розвитку, бо не втрачають своєї актуальності. Великий внесок у вирішення проблем створення нових багатопроцесорних архітектурних реалізацій та оцінки їх ефективності внесли Лебедєв С.А., Глушков В.М. , Капітонова Ю.В. , Самофалов К.Г., Забродін А.В. [1,2], Каляєв А.В. [3], Бурцев В.С. [4], Боюн В.П. [5], Митрофанов Ю.І. [6], Бошарін Г.П. [7], Коган Я.А [7,8], Менаске Д. та Алмейда В., Столингс У. [9].

Безліч завдань, розв'язуваних на багатопроцесорних системах, потребують розв'язання великих систем лінійних рівнянь з розрідженими матрицями

Причому, як правило, розв'язання завдань лінійної алгебри займає значну частину (50% і більше) часу розв'язання задачі взагалі[19]. Тому існує цілий ряд інструментальних засобів, покликаних распаралелити розв'язання СЛАР. Розглянемо бібліотеки методів, що використовують стандарт MPI і мають засіб для розв'язання СЛАР з розрідженими матрицями.

Огляд паралельних бібліотек

Aztec [10]

• метод сполучених градієнтів (CG),
• узагальнений метод мінімальних нев'язок (GMRES),
• квадратичний метод сполучених градієнтів (CGS),
• метод квазімінімальних нев'язок (TFQMR),
• метод бі-сполученого градієнта (BiCGSTAB) зі стабілізацією.

BlockSolve95

• Паралельна бібліотека для розв'язання розріджених систем лінійних рівнянь. Реалізована за допомогою MPI.
• Бібліотека розроблена в Argonne National Laboratory / MCS division. Розповсюджується безкоштовно.

P-Sparslib

• PSPARSLIB (A Portable Library of Parallel Sparse Iterative Solvers) — бібліотека паралельних ітеративних вирішувачів для розріджених систем лінійних рівнянь.

ScaLAPACK[11]

• Бібліотека ScaLAPACK включає процедури LAPACK, перероблених для використання на MPP-комп'ютерах: розв'язання систем лінійних рівнянь, обернення матриць, ортогональні перетворення, пошук власних значень та ін.
• Бібліотека ScaLAPACK розроблена з використанням PBLAS (паралельні версії BLAS рівнів 1,2,3) та комунікаційної бібліотеки BLACS.
• Підтримується на платформах IBM RS/6000 SP, Intel Paragon, SGI Origin 2000, і HP Exemplar, а також на кластерах робочих станцій. Може бути перенести на будь-яку платформу, де підтримується PVM або MPI.
• ScaLAPACK — спільний проект кількох організацій (Oak Ridge National Laboratory, Rice University, University of California at Berkeley University of California at LA University of Illinois, University of Tennessee at Knoxville)

PETSc[12]

• Набір процедур і структур даних для паралельного розв'язання наукових завдань з моделями, описуваними у вигляді диференціальних рівнянь з частинними похідними.
• Бібліотека реалізована за допомогою MPI.
• Підтримувані платформи: робочі станції Sun, RS/6000 включаючи SP, SGI IRIX — 32-бітові та 64-бітові версії, HP Exemplar, Cray T3D/T3E, DEC Alpha, Linux / FreeBSD / Windows NT на Intel.
• Бібліотека розроблена в Argonne National Laboratory / MCS division. Розповсюджується безкоштовно.
• Модуль KSP (Krylov subspace method — метод підпросторів Крилова) є серцем PETSc, оскільки він забезпечує уніфікований і ефективний доступ до всіх засобів для розв'язання систем лінійних алгебраїчних рівнянь (СЛАР).
• Модуль KSP надає багато популярних ітераційних методів на основі підпросторів Крилова: Conjugate Gradient, GMRES, CG-Squared, Bi-CG-stab та ін
• Модуль РС включає методи: Block Jacobi, Overlapping Additive Schwarz, ICC, ILU via BlockSolve95, ILU (k), LU (прямий метод, працює тільки на одному процесорі), Arbitrary matrix та ін

PLAPACK

• Пакет паралельних процедур лінійної алгебри. Включає паралельні версії процедур розв'язання систем лінійних рівнянь за допомогою LU і QR-розкладів, розкладання Холецького.
• Пакет PLAPACK реалізований з допомогою MPI. Включає інтерфейси для мов Fortran і С.
• Пакет PLAPACK розроблений в університеті шт. Техас (Austin). Доступний безкоштовно.
• Керівництво користувача було видано у видавництві MIT Press: Robert van de Geijn, "Using PLAPACK: Parallel Linear Algebra Package" (1997).
У ДонНТУ в останні роки подібної тематикою займалися магістранти:


1. Кучереносова Ольга (Керівник:проф.Башков Е.A. )
   Тема магістерської роботи: «Дослідження ефективності паралельних обчислювальних систем»
   
   
2. Міщук Юлія (Керівник: проф. Фельдман Л.П.)
   Тема магістерської роботи: «Аналіз ефективності обчислювальних систем з використанням Марковської моделі»
   
   
3. Горб Павло (Керівник: доц. Ладиженський Ю.В.)
   Тема магістерської роботи: «розв'язання великих систем лінійних алгебраїчних рівнянь в розподіленому обчислювальному середовищі»
   
   
4. Аль-Масрі Мохаммед Ріда (Керівник : доц. Ладиженський Ю.В.)
   Тема магістерської роботи: «Паралельні методи розв'язання СЛАР на обчислювальному кластері»

Побудова марковській моделі однорідного обчислювального кластеру

Одним із прикладів обчислювальних систем з розподіленою обробкою даних є кластери. Вони мають високу продуктивність і «живучість» обчислювальних ресурсів. Класифікація кластерних систем за спільним використанням одних і тих же дисків окремими вузлами є найпоширенішою [14,15]. Однією з основних проблем при побудові обчислювальних систем з розподіленою обробкою даних є вироблення рекомендацій для раціонального використання ресурсів цієї мережі. Ця задача виникає як при експлуатації, так і при проектуванні мережі. Для ефективної експлуатації кластерної системи необхідно побудувати її аналітичну модель і для кожного класу завдань визначити основні параметри обчислювального середовища. Ці моделі можна використовувати і для оптимізації обчислювальної системи на стадії проектування.

У даній роботі розглядається кластер зі спільним використанням дискового простору. Такі топології використовують СУБД Oracle Parallel Server і Informix [15]. Продуктивність таких систем може збільшуватися як шляхом нарощування числа процесорів і обсягів оперативної пам'яті в кожному вузлі кластеру, так і за допомогою збільшення кількості самих вузлів.

Принципова схема кластеру такого типу наведена на рис. 1.



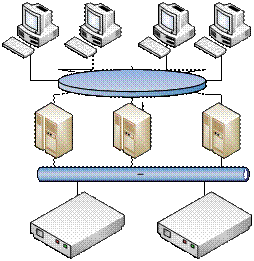
Рисунок 1 — Архітектура кластеру зі спільним використанням дискового простору


Спрощена модель кластеру зі спільним використанням дискового простору наведена на рис. 2

Вхідний вузол (керуючий сервер) рівномірно розподіляє між серверами додатків (виконують однакові програми) завдання. Кількість серверів — додатків — N1. Кожен з них може звернутися до даних, розташованим на дисках, кількість яких N2. Зважаючи на обмежених обчислювальних можливостей будемо вважати, що кількість завдань, обробляється такий обчислювальної системою не більше М.

Побудуємо дискретну Марківський модель. Так як кластер однорідний, представимо сервери, і, аналогічно, дискові накопичувачі багатоканальними пристроями. Вимоги, що надходять на обслуговування на сервери, надходять в обмежену чергу (не більше М), з якої на обслуговування вибираються за правилом «перший прийшов — перший обслужився».

Припустимо, завдання, оброблювані на такому кластері, однорідні і мають наступні характеристики:
p12 — імовірність запиту до одного з N1 серверів,
p23 — імовірність запиту до одного з N2 дисків,
p21 — ймовірність завершення обслуговування одним з N1 серверів,
p10 — ймовірність завершення обслуговування завдання,
q0 — імовірність появи нового завдання.




Рисунок 2 — Структурна схема Марковської моделі кластеру зі спільним використанням дискового простору
(Анімація: об'єм — 47 КБ, кількість кадрів — 12, кількість циклів повторення — 5, розмір — 702x136)


При побудові моделі використовується методика, запропонована в [16].

Алгоритм побудови дискретної Марковської моделі складається з двох частин: обчислень матриці перехідних ймовірностей і вектора стаціонарних ймовірностей.

При визначенні матриці перехідних ймовірностей використовуються наступні параметри:
N — кількість вузлів у моделюється системі (пристроїв або їх блоків)

M — кількість заявок у системі.



Кількість станів системи дорівнює кількості розміщень j завдань по N вузлів і визначається за формулою:


,

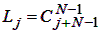загальна кількість станів обчислюється так:

.


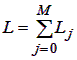Загальна кількість ненульових елементів матриці перехідних ймовірностей обчислюється як:





У таблиці наведено результати розрахунків частки ненульових елементів в матриці перехідних ймовірностей для моделі з трьома групами пристроїв N = 3 [17].



Кількість задач М
20	50	100	200
Розмірність матриці перехідних ймовірностей (кількість станів моделі)
1771 x 1771	23426 x 23426	176851 x 176851	1373701 x 1373701
Кількість ненульових елементів
1257408	94113953	2746496028	83871314553
Частка ненульових елементів в матриці перехідних ймовірностей
0.4009	0.1715	0.0878	0.0444

Розмірність матриць, що одержуються, залежить від кількості завдань системі, що моделюється.

Порядок отриманих матриць — від десятків і сотень тисяч до десятків мільйонів. Це викликано бажанням оперувати більш точними дискретними моделями, що дозволяють отримувати наближені розв'язання, більш близькі до рішень вихідних завдань, краще враховувати локальні особливості розглянутого процесу.

Вирішення таких завдань вимагає значних обчислювальних ресурсів, які можуть бути представлені паралельними комп'ютерами. Тому є актуальною проблема створення паралельних алгоритмів розв'язання даної задачі.

Важливою особливістю одержуваних матриць є той факт, що сума елементів по кожному рядку дорівнює одиниці, незалежно від їх числа. Звідси випливає ще одна складність обробки таких матриць: порядок елементів в матриці може сильно різнитися — від 0,5 до 10^-17. Тобто до подібних матриць не можна застосувати масштабування без втрат точності.

Наступною особливістю одержуваних матриць є те, що вони загального виду, тобто не можуть просто бути перетворені до одного зі стандартних видів: симетричному, стрічкового, блочно-діагонального з обрамленням і т.п., для яких вже розроблені ефективні паралельні алгоритми [18-21]

Отже, до алгоритму розв'язання СЛАР на таких розріджених матрицях висувається низка вимог:

• схема зберігання матриці повинна бути особливою: зберігаються тільки ненульові елементи та інформація про їх розташування у вихідній матриці [22];
• метод розв'язання СЛАР має запобігати втраті точності при обчисленнях
• паралельний алгоритм повинен бути ефективним і масштабованим.

очікувані результати

• розробити дискретну модель кластеру, за допомогою якої можна отримати основні характеристики обчислювального середовища;
• розробити новий паралельний алгоритм реалізації дискретної Марковської моделі однорідного кластера;
• отримати основні характеристики розпаралелювання;
• розробити паралельний алгоритм розв'язання СЛАР великої розмірності з розрідженими матрицями загального вигляду.

Важливе зауваження

При написанні даного автореферату магістерська робота ще не завершена. Остаточне завершення: грудень 2010р.

Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після зазначеної дати.

Література

1. Забродин А.В., Левин В.К. Опыт разработки параллельных вычислительных технологий, создание и развитие семейства МВС. // Тезисы докладов конференции «Высокопроизводительные вычисления и их приложения». 30 октября-2 ноября 2000 года, Черноголовка. — М.:МГУ, 2000. — с. 20-21.
2. Забродин А.В. Параллельные вычислительные технологии. Состояние и перспективы // Материалы первой молодежной школы «Высокопроизводительные вычисления и их приложения».
3. Каляев А. В., Левин И.И. Модульно-наращиваемые многопроцессорные системы со структурно-процедурной организацией вычислений. — М.: Янус-К, 2003. — 380 с.
4. Бурцев В.С. СуперЭВМ в России. История и перспективы. — ЭЛЕКТРОНИКА: НТБ, 2000, №4, с. 5–9.
5. Малиновский Б. Н., Боюн В.П., Козлов Л. Г. Введение в кибернетическую технику. Параллельные структуры и методы. — Киев: Наук. думка, 1989. — 245 с.
6. Митрофанов Ю.И. Основы теории сетей массового обслуживания. — Саратов: Изд-во Сарат.ун-та, 1993. — 116 с.
7. Бошарин Г.П., Бочаров П.П., Коган Я.А. Анализ очередей в вычислительных сетях. Теория и методы расчета. — М.: Наука, 1989.— 336 с.
8. Авен О.И., Гурин Н.Н., Коган Я.А. Оценка качества и оптимизация вычислительных систем. — М.: Наука,1982. — 464 с.
9. Столингс У. Структурная организация и архитектура компьютерных систем. — М.: Вильямс, 2002. — 893 с.
10. Аztec — a massively parallel iterative solver library for solving sparce linear systems [Электронный ресурс] / Интернет-ресурс. — Режим доступа: http://www.cs.sandia.gov/CRF/aztec1.html
11. ScaLAPACK Home Page [Электронный ресурс] / Интернет-ресурс. — Режим доступа: http://www.netlib.org/scalapack/scalapack_home.html
12. PETSc — Portable, Extensible Toolkit for Scientific Computation [Электронный ресурс] / Интернет-ресурс. — Режим доступа: http://www.mcs.anl.gov/petsc/petsc-as/
13. METIS — Family of Multilevel Partitioning Algorithms [Электронный ресурс] / Интернет-ресурс. — Режим доступа: http://glaros.dtc.umn.edu/gkhome/views/metis/
14. Спортак М., Франк Ч., Паппас Ч. и др. Высокопроизводительные сети. Энциклопедия пользователя. — К.: ДиаСофт, 1998. — 432 с.
15. Цилькер Б.Я., Орлов С.А. Организация ЭВМ и систем. — М: ПИТЕР, 2004. — 668 с.
16. Фельдман Л.П., Малинская Э.Б. Аналитическое моделирование вычислительных систем с приоритетным обслуживанием программ. //Электронное моделирование. — К., 1985. — №6.— с. 78-82.
17. Дяченко Т.Ф., Михайлова Т.В. Методы решения больших СЛАУ на разреженных матрицах общего вида // Тезизы доклада на IV международной научно-практической конференции молодых ученых, аспирантов,студентов «Современная информационная Украина: Информатика, Экономика, Философия», 13-14 мая 2010г., Государственный Университет информатики и искусственного интеллекта, Донецк
18. Попов А.В. Параллельные алгоритмы решения линейных систем с разреженными симметричными матрицами. // Штучний інтелект. — Д.,2006. — №4. — с. 248-257.
19. Химич А.Н., Попов А.В., Т.В. Чистякова, О.В. Рудич, Т.А. Герасимова. Исследование блочно-циклических алгоритмов на семействе кластеров СКИТ. // Проблеми програмування. — К., 2006. — № 2-3. — с. 177-183.
20. Игнатьев А.В., Ромашкин В.Н.. Анализ эффективности методов решения больших разреженных систем линейных алгебраических уравнений. // Интернет-вестник ВолгГАСУ. Сер.: Строит. информатика. 2008. — №3(6). — с. 1-7.
21. Ильин В.П. Проблемы высокопроизводительных технологий решения больших разреженных СЛАУ. // Вычислительные методы и программирование. — М., 2009. — №10. — с. 141-147.
22. Тьюарсон Р. Разреженные матрицы. Пер. с англ. М: Мир, 1977. — 189 с.
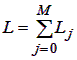