Tetyana Dyachenko
|

|
||||
 
|
Theme of master's thesis: "Research of the parallel algorithm for Markov models of computer systems"
Abstract for masters projectResearch of the parallel algorithm for
|
ObjectiveObjective is to develop an efficient parallel algorithm for constructing an analytic model of the cluster system, which will improve the performance of cluster systems based on the applying of the results of modeling. Research objectives:
BackgroundAnalysing methods of constructing high-performance cluster systems and tools for evaluating their performance demonstrates the complexity of solving the problem of analysis and synthesis of computing systems. Traditional solutions of this problem is insufficient and there is a need to develop new approaches to its solution.
Review of researchDue to the large number of created parallel computing systems (CS), work in this area requires further development and does not lose its relevance. A great contribution to solving the problems of new multiprocessor architecture implementations and evaluation of their effectiveness have made Lebedev S.A., Glushkov V.M. , Kapitonov U.V. , Samofalov K.G., Zabrodin A.V. [1,2], Kaliayev A.V. [3], Burtsev V.S. [4], Lund V.P. [5] Mitrofanov Y.B. [6], Bosharin G.P. [7], Kogan Y. [7,8], Menasco D. and Almeida, V., Kemeny J., Stolings W. [9]. A lot of problems solved on multiprocessor systems, require solving the linear system of equations, Ax = b, where, A is a user supplied n by n sparse matrix, b is a user supplied vector of length n, x is a vector of length n to be computed. Generally, the solution of linear algebra problems is a significant part (50% or more) time solutions throughout problem in general [19]. Software for Sparse Linear AlgebraAztecAztec is an iterative library that greatly simplifies the parallelization process solving the linear system of equations. A collection of data transformation tools are provided that allow for easy creation of distributed sparse unstructured matrices for parallel solution. Once the distributed matrix is created, computation can be performed on any of the parallel machines running Aztec: nCUBE 2, IBM SP2 and Intel Paragon, MPI platforms as well as standard serial and vector platforms. Aztec includes a number of Krylov iterative methods such as conjugate gradient (CG), generalized minimum residual (GMRES) and stabilized biconjugate gradient (BiCGSTAB) to solve systems of equations. These Krylov methods are used in conjunction with various preconditioners such as polynomial or domain decomposition methods using LU or incomplete LU factorizations within subdomains [10]. ScaLAPACKScaLAPACK is a project to provide parallel implementations for linear algebra. This project provides ScaLAPACK as dense and band matrix software. Especially, ScaLAPACK is designed for heterogeneous computing and implemented by using MPI and PVM for portability. PBLAS provides the fundamental operations of ScaLAPACK. PBLAS is a distributed memory version of BLAS that has similar functionalities to BLAS. ARPACK9 is software for solving large scale eigenvalue problems. This software is suitable for large sparse matrices or for a matrix A which require O(n) floating point operations but O(n2) operations when we calculate a matrix-vector product Ax [11]. PETScPETSc is a collection of lots of parallel scientific software which includes not only software for sparse matrices but also solvers for nonlinear equations, ODEs, PDEs, and etc. Interfaces for C, C++, Fortran, and Python are provided [12]. In DonNTU in recent years similar subject has been developed by masters:
Markov model of a homogeneous computing clusterOne example of computer systems with distributed processing are clusters. They have high performance and "survival" of computing resources. Classification of cluster systems is the most common [14,15]. One of the main problems is to develop recommendations for the rational use of resources of the network. This problem arises in the operation and the design of the network. For efficiently operation of the cluster system is necessary to build its analytical model and for each class of tasks determine the basic parameters of the computing environment. These models can be used to optimize the clusters on the design stage. In this paper we consider a cluster with the joint use of space. DB Oracle Parallel Server and Informix use such topology [15]. Performance of such systems can be increased either by increasing the number of processors and amount of RAM in each node of the cluster, and by increasing the number of nodes themselves. Schematic diagram of the cluster of this type is shown in Figure 1. 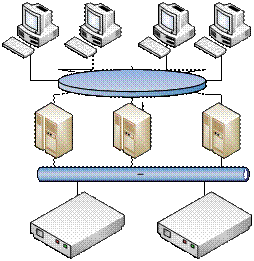 Figure 1 - Architecture of a cluster with sharing disk space The simplified model of the cluster with sharing disk space is shown in Fig. 2. Input node (management server) distributs tasks between the application servers. Number of application servers - N1. Each of them may apply to the data on the disks, which number are N2. Due to limited computing capacity, we assume that the number of tasks, processes the computer system is not more than M. Construct a discrete Markov model. Since a homogeneous cluster, we represent servers, and, similarly, disk drives as multi-channel devices. Tasks come for service on the servers (no more than M). The service is selected by the rule "first input — first output". For example, tasks that are processed in such a cluster are homogeneous and have the following characteristics:
 Figure 2 — Block diagram of Markov model of cluster with shared disk space (Animation: volume — 47 KB, the number of frames — 12, the number of cycles — 5, size — 702x136) The model constructing based on the method described in [16]. Algorithm of constructing a discrete Markov model consists of two parts: computing the matrix of transition probabilities and the vector of stationary probabilities. In determining the matrix of transition probabilities using the following parameters: number of states of the system equals the number of placements j tasks on N nodes: the total number of states is calculated as: 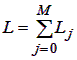 . . total number of nonzero elements of the matrix of transition probabilities is calculated as: The table shows the results of calculations of the proportion of nonzero elements in a matrix of transition probabilities for the model
with three groups of devices, N = 3 [17].
Dimension of a matrix depends on the amount of tasks in the simulated system. Order of matrices arises from tens or hundreds of thousands to tens of millions. This is caused by the desire to operate more accurate discrete models, allowing to obtain approximate solutions which are closer to the solutions of initial problems, it is better show local peculiarities of the process. Solving such problems requires significant computational resources, which can be represented by parallel computers. Therefore, there is an urgent problem of creating parallel algorithms for solving this problem. An important feature of a matrix is the fact that the sum of the elements of each row is unity, regardless of their number. Therefore the order of elements in the matrix can strongly vary — from 0,5 to 10 -17 . We can not apply zooming without loss of accuracy for such matrices. Another feature of the derived matrices is that they are unstructed,they can not simply be converted to one of the standard types: symmetric, tape, block-diagonal with bordering, etc., which have already developed efficient parallel algorithms [18-21]. Algorithm for solving the linear system of equation offers a number of requirements:
Expected results
Important:Master's work has not completed when this abstract was written. Completion of the master's work: December 2010. Full text of the work and materials on the topic can be obtained from the author or her supervisor after that date. Bibliography
| ||||||||||||||||||||||||||||||||