ДонНТУ  Портал магістрів
Русский  English

Реферат за темою випускної роботи

При написанні даного автореферату магістерська робота ще не завершена. Остаточне завершення: грудень 2014. Повний текст роботи та матеріали по темі можуть бути отримані у автора після зазначеної дати.

Зміст

Вступ

Навколишній світ – тривимірний, і тенденції створення надреалістичних зображень робить актуальним створення об'ємних дисплеїв. Для багатьох застосувань, наприклад, для вирішення задач розпізнавання образів, наведення літальних об'єктів на ціль, виконання хірургічних операцій, моделювання архітектурних споруд, завдань навчання, в телебаченні, кіно, розвагах робляться спроби створення дисплеїв для відображення об'ємних об'єктів [1].

Технології 3D дисплеїв у теперішній час розвиваються дуже динамічно. Розроблено безліч підходів до побудови 3D пристроїв відображення, які діляться на два види: стереоскопічні і об'ємні. Стереоскопічні 3D дисплеї формують окремі зображення для кожного ока. Такий принцип використовується у стереоскопах, відомих ще з початку XIX століття. Об'ємні дисплеї використовують різні фізичні явища для показу точок, що світяться, в межах деякого об'єму.

Створення і використання такого роду пристроїв вимагає розробки спеціальних апаратних і програмних засобів. Особливістю пристроїв відображення на базі об'ємних технологій є наявність об'ємного воксельного запам'ятовуючого пристрою – аналога растрової пам'яті двовимірних пристроїв відображення. При генерації тривимірного зображення в воксельної пам'яті програмними засобами створюється вокселізірованная модель реальних об'єктів, що складається із сукупності тривимірних графічних примітивів: відрізків тривимірних прямих, тривимірних площин, дуг, кіл, сферичних трикутників, еліпсоїдів і т.п. [2].

1. Актуальність теми

Зважаючи на збільшення обчислювальної потужності техніки та інтересу людини до візуалізації тривимірних образів, виникає необхідність у розробці ефективних алгоритмів генерації графічних примітивів, на базі яких можуть бути побудовані більш складні графічні об'єкти і сцени. Якщо для двовимірних дисплеїв існує безліч алгоритмів подання та обробки графічних об'єктів, то для тривимірних дисплеїв у теперішній час відсутні єдині стандарти подання графічної інформації. Для таких пристроїв не вироблені визначення типових 3D графічних примітивів і алгоритмів їх генерації.

Розробка нових алгоритмів генерації графічних образів у просторі тривимірних пристроїв відображення є актуальним завданням, вирішення якого може значно прискорити впровадження об'ємних тривимірних пристроїв відображення інформації в повсякденне життя людини.

2. Мета і задачі дослідження, заплановані результати

Мета роботи – розробка та програмна реалізація алгоритму генерації поверхонь другого порядку (сферичного трикутника) підвищеної продуктивності для об'ємних 3D пристроїв відображення.

Для досягнення мети поставлені такі завдання:

  • вивчити існуючі методи генерації графічних примітивів;
  • виконати аналіз способів подання сферичної поверхні в тривимірному просторі і запропонувати підхід для генерації воксельного розкладання сферичного трикутника;
  • розробити критерії оцінки точності воксельного розкладання;
  • розробити алгоритм оптимізації кількості вокселів в воксельного розкладанні;
  • протестувати алгоритм на різних наборах вхідних даних;
  • протестувати алгоритм на різних архітектурах і платформах з подальшим порівнянням часових витрат.

3. Огляд досліджень та розробок

Про те, що розглянута тема популярна як у вітчизняному, так і в світовому науковому товаристві свідчить велика кількість досліджень і розробок.

3.1. Огляд міжнародних джерел

Перші роботи, пов'язані з вокселізацією геометричних примітивів з'явилися наприкінці 1980-х років. Якщо перші алгоритми генерації воксельного зображення являли собою сканування простору сцени [3] (методом трасування променів), то вже на початку 1990-х американськими вченими Arie Kaufman і Sidney Wang в роботах [4,5] була запропонована технологія, заснована на фільтрації-згладжуванні, що дозволяє вирівнювати контурні нерівності об'єкта.

Однак для задач, в яких необхідна точність отриманої воксельної моделі, застосування згладжування неприпустимо. Новий алгоритм генерації воксельного розкладання був запропонований Nilo Stolte, який займався візуалізацією неявних поверхонь, в роботах [6,7,8]. Запропонований алгоритм грунтується на рекурсивному розбитті простору сцени за допомогою інтервальної арифметики, тобто вихідна модель представляється у вигляді октодерева. Такий підхід забезпечує більшу точність, можливість розпаралелювання і менші витрати пам'яті, проте продуктивність алгоритма ще далека від того, щоб використовувати дані підходи в інтерактивних додатках.

Збільшення продуктивності з використанням графічних прискорювачів було досліджено Shiaofen Fang і Hongsheng Chen в [9]. Високопродуктивний алгоритм для вокселізаціі твердих тіл представлений в [10]. Такий підхід заснований на конструктивній блочній геометрії, що дозволяє створити складну сцену або об'єкт за допомогою бітових операцій для комбінування декількох інших об'єктів. Перевагою цього алгоритму є те, що кожен вираз дерева сцени може бути виконано без використання обчислень і стеків.

З російських досліджень слід виділити роботу [11], в якій пропонується використовувати алгоритм багаторівневого відстеження променів для візуалізації моделей на базі функцій обурення, адаптований для завдання вокселізаціі.

3.2. Огляд локальних джерел

За межами ДонНТУ дослідження, пов'язані з воксельної графікою, не були виявлені.

У межах університету тема має широке поширення і регулярно обговорюється на конференціях і в публікаціях. Башков Є.А., Авксентьєва О.О., Аль-Орайкат Анас Махмуд у статті [2] розглядають способи побудови графічних примітивів. У роботі [12] Башков Є.А., Авксентьєва О.О., Аль-Орайкат Анас Махмуд, Хлопов Д.І. розглядають алгоритм генерації відрізка прямої.

У своїй роботі [13] Коніков А.В., Авксентьєва О.О. пропонують спеціалізований процесор для розкладання прямої в просторі 3D дисплея.

Алгоритм воксельного розкладання дуги розглянуто магістром Харченко М.О. [14]. Також пропонується використання технології CUDA для підвищення продуктивності генерації воксельного розкладання дуги.

У статті [15] Башков Є.А., Авксентьєва О.О., Половінкін О.О. описують алгоритм генерації воксельного розкладання просторового трикутника.

Магістр Хлопов Д.І. займався паралельними алгоритмами побудови воксельних моделей в реальному часі [16].

Магістр Радченко В.І. досліджував методи анімації воксельних моделей [17].

4. Алгоритм вокселизації сферичечного трикут

4.1. Постановка задачі

Задача воксельного розкладання сферичного трикутника може бути поставлена таким чином.

Нехай деяка область тривимірного евклідового простору, який відображається 3D дисплеєм, має вигляд тривимірного паралелепіпеда, Ω ∈ R3, 0 ≤ x ≤ X, 0 ≤ y ≤ Y, 0 ≤ z ≤ Z. З урахуванням можливості масштабування, будемо вважати, що X = Y = Z = H, тобто Ω – тривимірний куб.

Припустимо, що Ω заповнений вокселями – атомарними елементами, які відображаються 3D дисплеєм. Визначимо воксель як куб, орієнтований за осями Ω, з одиничним ребром. Безліч вокселів, що заповнюють Ωможна представити як тривимірний масив вокселів Vi,j,l. Причому, з одного боку, i, j, l – це індекси вокселя в масиві, що приймають значення 0,1,…Н, а с другой, они определяют координаты вокселя в Ω. Таким чином, воксель Vi,j,l це підмножина Ω, яке при відповідному виборі Н може бути визначене як i ≤ x ≤ i + (1-ε), j ≤ y ≤ j + (1-ε), l ≤ z ≤ l + (1-ε), де ε – нескінченно мала величина.

Сусідами деякого вокселя V(k) з координатами ik, jk, lk будемо вважати вокселі V(g), для яких виконується умова 1.

max{| ig - ik |, | jg - jk |, | lg - lk |} = 1(1)

При проведенні подальших міркувань в якості метрики на безлічі вокселів прийнята наступна функція

mg,k = | ig - ik | + | jg - jk | + | lg - lk |(2)

Визначимо координати VC центра вокселя Vi,j,l в Ω як

VCx = i + 0.5, VCy = j + 0.5, VCz = j + 0.5(3)

Припустимо, що сферичний трикутник лежить на сфері Φ з центром на початку координат і радіусом R. Трикутник утворений вершинами A = [xA, yA, zA], B = [xB, yB, zB], С = [xC, yC, zC], при цьому A ≠ B ≠ C і евклидова норма ||A|| = ||B|| = ||C|| = R.

Задачу воксельного розкладання сферичного трикутника ABC будемо розуміти як знаходження безлічі Θ вокселів, що належать сфері Φ і лежать всередині замкнутого відсіку цієї сфери, обмеженого відрізками великих кіл [18] AB, BC, CA.

Для будь-якого з вокселів V(k) в розкладанні необхідно забезпечити наступні умови:

  • хоча б одна точка сфери належить вокселю V(k) або, що эквівалентно, довжина перпендикуляра, опущеного з центру V(k) на Φ не повинна перевершувати 0,866 (з урахуванням одиничного ребра вокселя);
  • вокселі повинні лежати усередині області сфери Φ, що обмежуеться відрізками великих кіл AB, BC, CA;
  • кількість вокселів в розкладанні має бути мінімально, тобто для будь-якого V(k) з Θ (який не представляє кордон AB, BC, CA примітиву) мав не більше 8 сусідів;
  • будь-який V(k) з Θ (який не представляє кордон AB, BC, CA примітиву) мав не менше 8 сусідів – умова забезпечення відсутності «прогалин» між вокселів розкладання.

4.2. Загальний алгоритм воксельної декомпозиції сферичного трикутника

Нехай є вершини A, B, C, які описують сферичний трикутник. Для знаходження воксельного розкладання такого трикутника можна використовувати наступний підхід.

На початковому етапі формуються три динамічних списки:

  • список вокселів, що входять до розкладання (результуючі вокселі);
  • список вокселів для перевірки (у вокселів можуть бути сусіди, що входять до результуючого розкладання);
  • список відбракованих вокселів (вокселі не входять до результуючого розкладання).

При ініціалізації до списку результуючих вокселів і списку вокселів для перевірки заносяться вокселі, що відповідають вершинам A, B і С. Поки список вокселів для перевірки не порожній, з нього вибирається і віддаляється перший елемент, обчислюються координати його 26 сусідів і, якщо сусід ще не був включений в результуючий список і не був відкинутий, то для нього перевіряється потенційна приналежність сферичному трикутнику і відстань до поверхні сфери. Якщо перевірка успішно виконана, то такий воксель заноситься до списку результуючих вокселів і список вокселів для перевірки, інакше – до списку відбракованих вокселів. Процес завершується коли список вокселів для перевірки стає порожнім.

Таким чином, в списку результуючих вокселів знаходяться координати точок вокселів, які входять до воксельного розкладання заданого сферичного трикутника АВС. Для отримання оптимального розкладання такий список необхідно оптимізувати шляхом видалення зайвих вокселів. Для цього вокселі упорядковуються по збільшенню відстані до поверхні сфери, а потім для кожного з вокселів проводиться перевірка кількості сусідів , що входять до розкладання. Якщо таких сусідів більше 8, то віддаляються ті з них, відстань яких до поверхні найбільша. Алгоритм може бути представлений на псевдомові таким чином.

Введення вершин трикутника А, B, C;
Список_результуючих_вокселів = null;
Список_вокселів_для_перевірки = null;
Список_відбракованих_вокселів = null;
for(i = 0; i < 3; i++){
    Список_результуючих_вокселів.Додати(вершини[i]);
    Список_вокселів_для_перевірки.Додати(вершини[i]);
}
while(Список_вокселів_для_перевірки не порожній){
    Поточний_воксель = Список_вокселів_для_перевірки.Перший();
    Сусіди = Поточний_воксель.Отримати_сусідів();
    for(i = 0; i < 26; i++){
        if(Сусіди[i] відбракований || Сусіди[i] у результаті)
            continue;
        if(Сусіди[i] знаходиться у трикутнику && Сусіди[i] знаходиться на поверхні сфери) {
            Список_результуючих_вокселів.Додати(Сусіди[i]);
            Список_вокселів_для_перевірки.Додати(Сусіди[i]);
        } else {
            Список_відбракованих_вокселів.Додати(Сусіди[i]);
        }
    }
}
Список_результуючих_вокселів.Сортувати_по_відстані_до_поверхні();
foreach(Воксель із Списку_результуючих_вокселів){
    Воксель.Оптимізувати_кількість_сусідів();
}
Виведення Cписка_списка результуючих вокселів;

Слід зазначити, що в розглянутому алгоритмі найбільшу обчислювальну складність має процес перевірки належності точки сферичному трикутнику, тому важливо вибрати такий метод, який дозволив би мінімізувати апаратні та часові витрати.

4.3. Методи перевірки приналежності сферичному трикутнику

Припустимо, що знайдено деякий q-й воксель розкладання, що задовольняє умовам. Наступні вокселі шукаються серед вокселів-претендентів ( сусідів ) з метрикою не більш 1.

Таблиця 1 – Прирощення координат для вокселів-претендентів

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
x -1 -1 -1 -1 -1 -1 -1 -1 -1 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1
y -1 -1 -1 0 0 0 1 1 1 -1 -1 -1 0 0 1 1 1 -1 -1 -1 0 0 0 1 1 1
z -1 0 1 -1 0 1 -1 0 1 -1 0 1 -1 1 -1 0 1 -1 0 1 -1 0 1 -1 0 1

Після того, як знайдені 26 вокселів-претендентів, потрібно вибрати з них ті, які потенційно належать результуючій множині вокселів. Для знаходження таких вокселів можна використовувати один з наступних підходів.

1. Перевірка приналежності сферичному трикутнику за площею

Нехай слід перевірити приналежність точки Р сферичному трикутнику АВС. Положення точки Р в трикутнику зображено на малюнку 1.

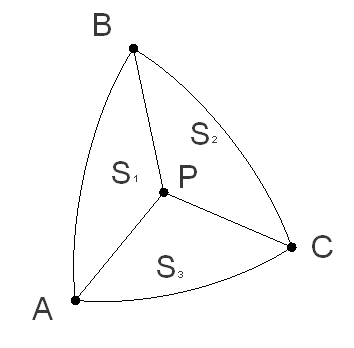
Положення точки Р в трикутнику

Малюнок 1 – Положення точки Р в трикутнику

Для вирішення завдання формуються три трикутника, що лежать на поверхні сфери: ABP, BCP, ACP. Потім обчислюються площі цих трикутників: S 1, S2 і S 3 відповідно. Після цього порівнюється сума площ S1, S2, S3 з площею трикутника S ABC. Якщо точка Р лежить у трикутнику ABC, то сума площ буде дорівнювати площі S ABC. Якщо ж точка не належить трикутнику, сума площ S 1, S2 і S3 перевищить площу трикутника ABC.

Для знаходження площі кожного сферичного трикутника використовується формула 4.

S = R2 (α + β + γ - π) (4)

В формулі α, β, γ – кути сферичного трикутника. Кут сферичного трикутника вимірюється величиною двогранного кута між площинами, в яких лежать сторони цього кута [19]. Кути сферичного трикутника зображені на малюнку 2.

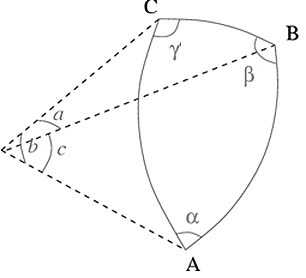
Кути і сторони сферичного трикутника

Малюнок 2 – Кути і сторони сферичного трикутника

На малюнку 2 a, b, c – сторони сферичного трикутника. Сторона сферичного трикутника вимірюється величиною центрального кута, що спирається на неї [19]. Кути сферичного трикутника обчислюються за формулами 5.

α = arccos((cos( a ) - cos( b ) cos ( c )) / sin( b ) sin( c ))
β = arccos((cos( b ) - cos( c ) cos ( a )) / sin( c ) sin( a ))(5)
γ = arccos((cos( c ) - cos( a ) cos ( b )) / sin( a ) sin( b ))

Сторони сферичного трикутника знаходяться шляхом обчислення кутів, утворених векторами, проведеними з центру сфери до вершини сферичного трикутника.

2. Перевірка приналежності сферичному трикутнику по площинах

Серед знайдених вокселів-претендентів вибираються ті, центри яких розташовані між трьома площинами, кожна з яких утворена однією зі сторін сферичного трикутника і точкою центру сфери, тобто необхідно побудувати додаткові площини AOB, BOC, COA, як це зображено на малюнку 3.

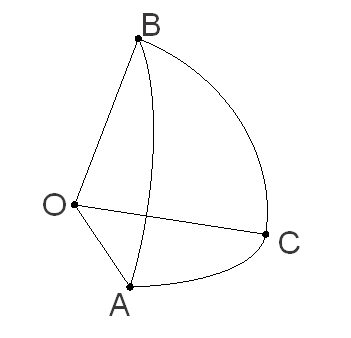
Додаткові площини

Малюнок 3 – Додаткові площини

Кожна така площина має рівняння Ax + By + Cz + D = 0 , де А, B, C, D – постійні, причому А, B і C одночасно не рівні нулю. Знаючи координати вершин трикутника і точки центра сфери, можна знайти коефіцієнти площин за формулами 6.

A = y1 (z2 - z3) + y2 (z3 - z1) + y3 (z1 - z2)
B = z1 (x2 - x3) + z2 (x3 - x1) + z3 (x1 - x2)
C = x1 (y2 - y3) + x2 (y3 - y1) + x3 (y1 - y2)(6)
-D = x1 (y2 z3 - y3 z2) + x2 (y3 z1 - y1 z3) + x3 (y1 z2 - y2 z1)

Належність вокселя-претендента сферичному трикутнику визначається його положенням щодо трьох додаткових площин. Так, якщо воксель-претендент належить сферичному трикутнику, то підставивши координати його центру в рівняння всіх трьох площин, ми отримаємо позитивне значення. Якщо ж при підстановці координат центру в рівняння хоча б одне зі значень – негативне, розглянутий воксель не належить сферичному трикутнику.

На малюнку 4 представлений приклад роботи алгоритму генерації воксельного розкладання сферичного трикутника, візуалізований за допомогою пакету Mathematica 9.

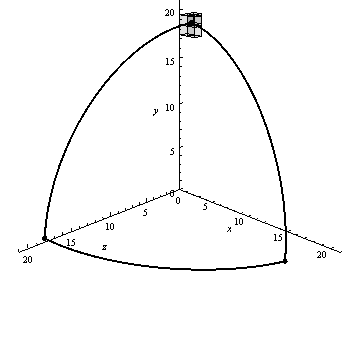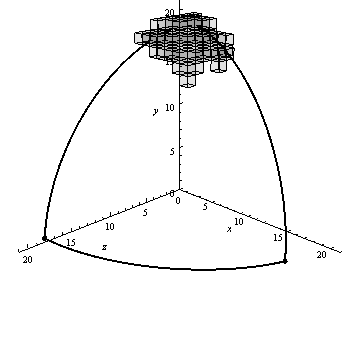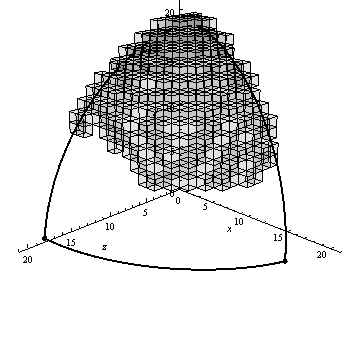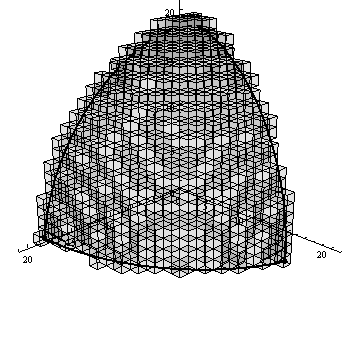
Робота алгоритму вокселізаціі сферичного трикутника

Малюнок 4 – Робота алгоритму вокселізаціі сферичного трикутника (анімація: 13 кадрів, 10 циклів повторення, 67.8 кБ)

4.4. Експериментальні досліждення алгоритму воксельної декомпозиції сферичного трикутника

Експериментальне дослідження запропонованого алгоритму (з перевіркою приналежності точки трикутнику двома методами) полягало в генерації 1000 сферичних трикутників в ? з H = 20. Вершини трикутників генерувалися за допомогою генератора псевдовипадкових чисел. Експерименти виконувалися на персональному комп'ютері CPU Intel (R) Core (TM) i5– 3317U CPU@1.70GHz, 8ГБ ОЗУ. Для вимірювання часу роботи алгоритму на початку і в кінці роботи програми записувалися мітки часу. В якості часу виконання програми була використана різниця початкової і кінцевої міток, хоча даний показник не можна вважати абсолютно точним (на практиці такий підхід дає недостатньо точні результати). Узагальнені результати експериментів наведені в таблиці 2 .

Таблиця 2 – Результати єкспериментального дослідження

Метод перевірки площею Метод перевірки площинами
Час генерації 1000 трикутників, мс 261 620 226 566
Кількість згенерованих вокселів 586 090 586 090
Середній час генерації трикутника, мс 261,62 226,56
Середній час генерації вокселя, мс 0,446 0,387

Виходячи з даних, наведених у таблиці 2, можна зробити висновок про те, що метод перевірки площинами в середньому на 15% швидше методу перевірки площею.

Крім того, результат експерименту показує, що робота методу перевірки належності точки сферичному трикутнику за допомогою допоміжних площин виявилася швидше методу перевірки площею в 96% варіантів трикутників. Це пояснюється тим, що для даного методу потрібно менший обсяг обчислень, тому що на початку алгоритму проводиться розрахунок коефіцієнтів трьох площин, а потім у циклі у знайдені рівняння підставляються координати конкретних точок. Для методу перевірки за допомогою площ на початковій етапі можливе лише обчислення загальної площі сферичного трикутника, а потім в циклі відбувається обчислення площ трьох трикутників, утворених конкретною заданою точкою і вершинами сферичного трикутника. Очевидно, що обчислення значення рівняння в точці менш трудомісткий процес, ніж розрахунок площі сферичного трикутника.

Висновки

У роботі запропоновано підхід для вирішення завдання вокселізаціі сферичного трикутника.

У запропонованому алгоритмі розглянуті два методи перевірки точки на приналежність сферичному трикутнику і проведено їх порівняльний аналіз.

Запропонований у роботі підхід може розглядатися тільки як початковий, що вимагає додаткових досліджень в напрямку мінімізації кількості вокселів в генерованому розкладанні і його оптимізації з метою скорочення як тимчасових витрат, так і необхідної пам'яті.

Подальша робота буде спрямована на оптимізацію алгоритму, а також на розробку алгоритмів генерації воксельного розкладання для інших поверхонь другого порядку.

Перелік посилань

  1. Томилин М.Г., Невская Г.Е. Дисплеи на жидких кристаллах: Учебное пособие. – СПб: СПбГУ ИТМО, 2010. – c.73.
  2. Башков Е.А., Авксентьева О.А., Аль-Орайкат Анас М. К построению генератора графических примитивов для трехмерных дисплеев [Текст]. В сб. Наукові праці Донецького національного технічного університету, серія "Проблеми моделювання та автоматизації проектування динамічних систем". Вип. 7 (150). – Донецьк, ДонНТУ. – 2008 .– с. 203–214.
  3. Kaufman, A., Shimony, E., '3D Scan-Conversion Algorithms for Voxel-Based Graphics', Proc. ACM Workshop on Interactive 3D Graphics, Chapel Hill, NC, October 1986, pp. 45–76.
  4. S.Wang, A. Kaufman. Volume sampled voxelization of geometric primitives. Proceedings of Visualization’ 1993, pp. 78–84.
  5. S.Wang, A. Kaufman. Volume-sampled 3D modeling. Computer Graphics and Applications, 1994, pp. 26–32.
  6. N. Stolte, R. Caubet. Discrete Ray-Tracing of Huge Voxel Spaces Computer Graphics Forum, 1995.
  7. N. Stolte, R. Caubet. Comparison between different rasterization methods for implicit surfaces. Visualization and Modeling, 1997.
  8. N. Stolte, A. Kaufman. Parallel spatial enumeration of implicit surfaces using interval arithmetic for octree generation and its direct visualization. Implicit Surfaces', 1998.
  9. Shiaofen Fang, Hongsheng Chen. Hardware accelerated voxelization. Computers & Graphics, 2000, pp. 433–442.
  10. Sema Koca, Ulus Cevikb. A new approach for the voxelization of volumetric CSG graphs, 2004, pp. 245–255.
  11. Катасонов А.В., Вяткин С.И., Долговесов Б.С. Вокселизация функциональных форм [Електронний ресурс]. Режим доступу: http://www.graphicon.ru/html/2005/proceedings/papers/Katasonov_Vyatkin.pdf.
  12. Башков Е.А., Авксентьева О.А., Аль-Орайкат Анас Махмуд, Хлопов Д.И. Генератор отрезков прямых повышенной производительности для трехмерных дисплеев. В сб. Научные труды ДонНТУ. Серия «Информатика, кибернетика и вычислительная техника». – 2010. – Вып. 11(164). – с. 100–106.
  13. Коников А.В., Авксентьева О.А. Специализированный процессор для разложения пространственной прямой для объемных 3D дисплеев [Електронний ресурс]. Режим доступу: http://iuskm.donntu.ru/pdf/vol1/Section3.pdf#page=16.
  14. Харченко Н.О. Структурно-алгоритмическая организация устройств генерации произвольных дуг и секторов в 3D пространстве для объёмных дисплеев [Електронний ресурс]. Режим доступу: http://masters.donntu.ru/2011/fknt/hartchenko/diss/index.htm.
  15. Башков Е.А., Авксентьева О.А., Половинкин О.А. Базовый алгоритм воксельного разложения пространственного треугольника. В сб. Наукові праці Донецького національного технічного університету. Серiя «Проблеми моделювання та автоматизації проектування» (МАП-2011). Випуск: 10 (197) – Донецьк: ДонНТУ. – 2011. – 290 с.
  16. Хлопов Д.И. Параллельные методы и алгоритмы построения воксельных моделей в реальном времени [Електронний ресурс]. Режим доступу: http://masters.donntu.ru/2012/fknt/khlopov/diss/index.htm.
  17. Радченко В.И. Исследование методов анимации воксельных моделей [Електронний ресурс]. Режим доступу: http://masters.donntu.ru/2012/fknt/radchenko/diss/index.htm.
  18. Большой круг [Електронний ресурс]. Режим доступу: http://ru.wikipedia.org/wiki/Большой_круг
  19. Сферический треугольник [Електронний ресурс]. Режим доступу: http://ru.wikipedia.org/wiki/Сферический_треугольник
Резюме  Біографія