Реферат по теме выпускной работы
При написании данного автореферата магистерская работа ещё не завершена. Окончательное завершение: декабрь 2014 г. Полный текст работы и материалы по теме могут быть получены у автора после указанной даты.
Содержание
- Введение
- 1. Актуальность темы
- 2. Цель и задачи исследования, планируемые результаты
- 3. Обзор исследований и разработок
- 3.1 Обзор международных источников
- 3.2 Обзор локальных источников
- 4. Алгоритм вокселизации сферического треугольника
- 4.1 Постановка задачи
- 4.2 Базовый алгоритм воксельного разложения сферического треугольника
- 4.3 Методы проверки принадлежности точки сферическому треугольнику
- 4.4 Экспериментальные исследования алгоритма воксельного разложения сферического треугольника
- Выводы
- Список источников
Введение
Окружающий нас мир – трехмерный, и тенденции создания сверхреалистических дисплеев делает актуальным создание объемных дисплеев. Для многих применений, например, для решения задач распознавания образов, наведения летательных объектов на цель, выполнения хирургических операций, моделирования архитектурных сооружений, задач обучения, в телевидении, кино, развлечениях и др. предпринимаются попытки создания дисплеев для отображения объемных объектов [1].
Технологии 3D дисплеев в настоящее время развиваются очень динамично. Разработано множество подходов к построению 3D устройств отображения, которые делятся на два вида: стереоскопические и объемные. Стереоскопические 3D дисплеи формируют отдельные изображения для каждого глаза. Такой принцип используется в стереоскопах, известных ещё с начала XIX века. Объёмные дисплеи используют различные физические явления для показа светящихся точек в пределах некоторого объёма.
Создание и использование такого рода устройств требует разработки специальных аппаратных и программных средств. Особенностью устройств отображения на базе объемных технологий является наличие объемного воксельного запоминающего устройства — аналога растровой памяти двумерных устройств отображения. При генерации трехмерного изображения в воксельной памяти программными средствами создается «вокселизированная» модель реальных объектов, состоящая из совокупности трехмерных графических примитивов: отрезков трехмерных прямых, трехмерных плоскостей, дуг, окружностей, сферических треугольников, эллипсоидов и т.п. [2].
1. Актуальность темы
Ввиду увеличения вычислительной мощности техники и интереса человека к визуализации трехмерных образов, возникает необходимость в разработке эффективных алгоритмов генерации графических примитивов, на базе которых могут быть построены более сложные графические объекты и сцены. Если для двумерных дисплеев существует множество алгоритмов представления и обработки графических объектов, то для трехмерных дисплеев в настоящее время отсутствуют единые стандарты представления графической информации. Для таких устройств не выработаны определения типовых 3D графических примитивов и алгоритмов их генерации.
Разработка новых алгоритмов генерации графических образов в пространстве трехмерных устройств отображения является актуальной задачей, решение которой может значительно ускорить внедрение объемных трехмерных устройств отображения информации в повседневную жизнь человека.
2. Цель и задачи исследования, планируемые результаты
Цель работы – разработка и программная реализация алгоритма генерации поверхностей второго порядка (сферического треугольника) повышенной производительности для объемных 3D устройств отображения.
Для достижения цели поставлены следующие задачи:
- изучить существующие методы генерации графических примитивов;
- выполнить анализ способов представления сферической поверхности в трехмерном пространстве и предложить подход для генерации воксельного разложения сферического треугольника;
- разработать критерии оценки точности воксельного разложения;
- разработать алгоритм оптимизации количества вокселей в воксельном разложении;
- протестировать алгоритм на различных наборах входных данных;
- протестировать алгоритм на различных архитектурах и платформах с дальнейшим сравнением временных затрат.
3. Обзор исследований и разработок
О том, что рассматриваемая тема популярна как в отечественном, так и в мировом научном сообществе свидетельствует большое количество исследований и разработок.
3.1. Обзор международных источников
Первые работы, связанные с вокселизацией геометрических примитивов появились в конце 1980-х годов. Если исходные алгоритмы генерации воксельного изображения представляли собой построчное сканирование пространства сцены [3] (методом трассировки лучей), то уже в начале 1990-х американскими учеными Arie Kaufman и Sidney Wang в работах [4,5] была предложена технология, основанная на фильтрации–сглаживании, позволяющая выравнивать контурные неровности объекта.
Однако для задач, в которых необходима точность полученной воксельной модели, применение сглаживающей технологии недопустимо. Новый алгоритм генерации воксельного разложения был предложен Nilo Stolte, который занимался визуализацией неявных поверхностей, в работах [6,7,8]. Предложенные алгоритм основывается на рекурсивном разбиении пространства сцены с помощью интервальной арифметики, т.е. результирующая модель представляется в виде октодерева. Такой подход обеспечивает большую точность, возможность распараллеливания и меньшие затраты памяти, однако производительность алгоритмов еще далека от того, чтобы использовать данные подходы в интерактивных приложения.
Увеличение производительности с использованием графических ускорителей было исследовано Shiaofen Fang и Hongsheng Chen в [9]. Высокопроизводительный алгоритм для вокселизации твердых тел представлен в [10]. Такой подход основан на конструктивной блочной геометрии, что позволяет создать сложную сцену или объект с помощью битовых операций для комбинирования нескольких иных объектов. Достоинством этого алгоритма является то, что каждое выражение дерева сцены может быть выполнено без использования вычислений и стеков.
Из российских исследований следует выделить работу [11], в которой предлагается использовать алгоритм многоуровневого отслеживания лучей для визуализации моделей на базе функций возмущения, адаптированный для задачи вокселизации.
3.2. Обзор локальных источников
За пределами ДонНТУ исследования, связанных с воксельной графикой, не были обнаружены.
В пределах университета тема имеет широкое распространение и регулярно обсуждается на конференциях и в публикациях. Башков Е.А., Авксентьєва О.О., Аль-Орайкат Анас Махмуд в статье [2] рассматривают способы построения графических примитивов. В работе [12] Башков Є.А., Авксентьева О.А., Аль-Орайкат Анас Махмуд, Хлопов Д.И. рассматривают алгоритм генерации отрезка прямой.
В своей статье [13] Коников А.В., Авксентьева О.А. предлагают специализированный процессор для разложения прямой в пространстве 3D дисплея.
Алгоритм воксельного разложения дуги рассмотрен магистром Харченко Н.О. [14]. Также предлагается использование технологии CUDA для повышения производительсности генерации воксельного разложения дуги.
В статье [15] Башков Е.А., Авксентьева О.А., Половинкин О.А. описывают алгоритм генерации воксельного разложения пространственного треугольника.
Магистр Хлопов Д.И. занимался параллельными алгоритмами построения воксельных моделей в реальном времени [16].
Магистр Радченко В.И. исследовал методы анимации воксельных моделей [17].
4. Алгоритм вокселизации сферического треугольника
4.1. Постановка задачи
Задача воксельного разложения сферического треугольника может быть поставлена следующим образом.
Пусть некоторая область трехмерного евклидова пространства, которое отображается 3D дисплеем, имеет вид трехмерного параллелепипеда, Ω ∈ R3, 0 ≤ x ≤ X, 0 ≤ y ≤ Y, 0 ≤ z ≤ Z. С учетом возможности масштабирования, будем считать, что X = Y = Z = H, то есть Ω – трехмерный куб.
Положим, что Ω заполнен вокселями – атомарными элементами, которые отображаются 3D дисплеем. Определим воксель как куб, ориентированный по осям Ω, с единичным ребром. Множество вокселей, заполняющих Ω можно представить как трехмерный массив вокселей Vi,j,l. Причем, с одной стороны, i, j, l – это индексы вокселя в массиве, принимающие значения 0,1,…Н, а с другой, они определяют координаты вокселя в Ω. Таким образом, воксель Vi,j,l это подмножество Ω, которое при соответствующем выборе Н может быть определено как i ≤ x ≤ i + (1-ε), j ≤ y ≤ j + (1-ε), l ≤ z ≤ l + (1-ε), где ε – бесконечно малая величина.
Соседями некоторого вокселя V(k) с координатами ik, jk, lk будем считать воксели V(g), для которых выполняется условие 1.
При проведении дальнейших рассуждений в качестве метрики на множестве вокселей принята следующая функция
Определим координаты VC центра вокселя Vi,j,l в Ω как
Допустим, что сферический треугольник лежит на сфере Φ с центром в начале координат и радиусом R. Треугольник образован вершинами A = [xA, yA, zA], B = [xB, yB, zB], С = [xC, yC, zC], при этом A ≠ B ≠ C и евклидова норма ||A|| = ||B|| = ||C|| = R.
Задачу воксельного разложения сферического треугольника ABC будем понимать как нахождение множества Θ вокселей принадлежащих сфере Φ и лежащих внутри замкнутого отсека(участка) этой сферы, ограниченного отрезками больших кругов [18] AB, BC, CA.
Для любого из вокселей V(k) в разложении необходимо обеспечить следующие условия:
- хотя бы одна точка сферы принадлежит вокселю V(k) или, что эквивалентно, длина перпендикуляра, опущенного из центра V(k) на Φ не должна превосходить 0,866 (с учетом единичного ребра вокселя);
- воксели должны лежать внутри области сферы Φ, ограничиваемой отрезками больших кругов AB, BC, CA;
- количество вокселей в разложении должно быть минимально, то есть для любого V(k) из Θ (не представляющего границы AB, BC, CA примитива) имел не более 8 соседей;
- любой V(k) из Θ (не представляющий границы AB, BC, CA примитива) имел не менее 8 соседей – условие обеспечения отсутствия «пробелов» между вокселями разложения.
4.2. Базовый алгоритм воксельного разложения сферического треугольника
Пусть имеются вершины A, B, C, которые описывают сферический треугольник. Для нахождения воксельного разложения такого треугольника можно использовать следующий подход.
На начальном этапе формируются три динамических списка:
- список вокселей, входящих в разложение (результирующие воксели);
- список вокселей для проверки (у вокселей могут быть соседи, входящие в результирующее разложение);
- список отбракованных вокселей (воксели не входят в результирующее разложение).
При инициализации в список результирующих вокселей и список вокселей для проверки заносятся воксели, соответствующие вершинам A, B и С. Пока список вокселей для проверки не пуст, из него выбирается и удаляется первый элемент, вычисляются координаты его 26 соседей и, если сосед еще не был включен в результирующее множество и не был отвергнут, то для него проверяется потенциальная принадлежность сферическому треугольнику и расстояние до поверхности сферы. Если проверка успешно выполнена, то такой воксель заносится в список результирующих вокселей и список вокселей для проверки, иначе – в список отбракованных вокселей. Процесс завершается когда список вокселей для проверки становится пустым.
Таким образом, в списке результирующих вокселей находятся координаты точек вокселей, которые входят в воксельное разложение заданного сферического треугольника АВС. Для получения оптимального разложения такой список необходимо оптимизировать путем удаления лишних вокселей. Для этого воксели упорядочиваются по увеличению расстояния до поверхности сферы, а затем для каждого из вокселей производится проверка количества соседей, входящих в разложение. Если таких соседей больше 8, то удаляются те из них, расстояние до поверхности которых наибольшее. Вышеизложенный алгоритм может быть представлен на псевдоязыке следующим образом.
Ввод вершин треугольника А, B, C;
Список_результирующих_вокселей = null;
Список_вокселей_для_проверки = null;
Список_отбракованных_вокселей = null;
for(i = 0; i < 3; i++){
Список_результирующих_вокселей.Добавить(вершины[i]);
Список_вокселей_для_проверки.Добавить(вершины[i]);
}
while(Cписок_вокселей_для_проверки не пуст){
Текущий_воксель = Cписок_вокселей_для_проверки.Первый();
Соседи = Текущий_воксель.Получить_соседей();
for(i = 0; i < 26; i++){
if(Соседи[i] отбракован || Соседи[i] в результате)
continue;
if(Соседи[i] находится в треугольнике && Соседи[i] находится на поверхности сферы) {
Список_результирующих_вокселей.Добавить(Соседи[i]);
Список_вокселей_для_проверки.Добавить(Соседи[i]);
} else {
Список_отбракованных_вокселей.Добавить(Соседи[i]);
}
}
}
Список_результирующих_вокселей.Сортировать_по_расстоянию();
foreach(Воксель из Списка_результирующих_вокселей){
Воксель.Оптимизировать_количество_соседей();
}
Вывод Cписка_результирующих_вокселей;
Следует отметить, что в рассмотренном алгоритме наибольшую вычислительную сложность имеет процесс проверки принадлежности точки сферическому треугольнику, поэтому важно выбрать такой метод, который позволил бы минимизировать аппаратные и временные затраты.
4.3. Методы проверки принадлежности точки сферическому треугольнику
Предположим, что найден некоторый q-й воксель разложения, удовлетворяющий условиям. Следующие воксели ищутся среди вокселей–претендентов (соседей
) с метрикой не больше 1. Приращения координат для вокселей-претендентов приведены в таблице 1.
Таблица 1 – Приращение координат для вокселей-претендентов
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| y | -1 | -1 | -1 | 0 | 0 | 0 | 1 | 1 | 1 | -1 | -1 | -1 | 0 | 0 | 1 | 1 | 1 | -1 | -1 | -1 | 0 | 0 | 0 | 1 | 1 | 1 |
| z | -1 | 0 | 1 | -1 | 0 | 1 | -1 | 0 | 1 | -1 | 0 | 1 | -1 | 1 | -1 | 0 | 1 | -1 | 0 | 1 | -1 | 0 | 1 | -1 | 0 | 1 |
После того, как найдены 26 вокселей-претендентов, нужно выбрать из них те, которые потенциально принадлежат результирующему множеству вокселей. Для нахождения таких вокселей можно использовать один из следующих подходов.
1. Проверка принадлежности сферическому треугольнику по площади
Пусть следует проверить принадлежность точки Р сферическому треугольнику АВС. Положение точки Р в треугольнике изображено на рисунке 1.
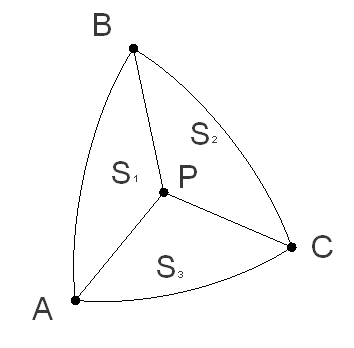
Рисунок 1 – Положение точки Р в треугольнике
Для решения задачи формируются три треугольника, лежащих на поверхности сферы: ABP, BCP, ACP. Затем вычисляются площади этих треугольников: S1, S2 и S3 соответственно. После этого сравнивается сумма площадей S1, S2, S3 с площадью треугольника SABC. Если точка Р лежит в треугольнике ABC, то сумма площадей будет равна площади SABC. Если же точка не принадлежит треугольнику, сумма площадей S1, S2 и S3 превысит площадь треугольника ABC.
Для нахождения площади каждого сферического треугольника используется формула 4.
В формуле α, β, γ – углы сферического треугольника. Угол сферического треугольника измеряется величиной двугранного угла между плоскостями, в которых лежат стороны этого угла [19]. Углы сферического треугольника изображены на рисунке 2.
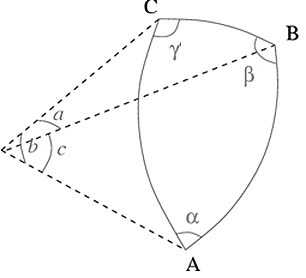
Рисунок 2 – Углы и стороны сферического треугольника
На рисунке 2 a, b, c – стороны сферического треугольника. Сторона сферического треугольника измеряется величиной опирающегося на неё центрального угла [19]. Углы сферического треугольника вычисляются по формулам 5.
Стороны сферического треугольника находятся путем вычисления углов, образованных векторами, проведенными из центра сферы в вершины сферического треугольника.
2. Проверка принадлежности сферическому треугольнику по плоскостям
Среди найденных вокселей–претендентов выбираются те, центры которых расположены между тремя плоскостями, каждая из которых образована одной из сторон сферического треугольника и точкой центра сферы, то есть необходимо построить дополнительные плоскости AOB, BOC, COA, как это изображено на рисунке 3.
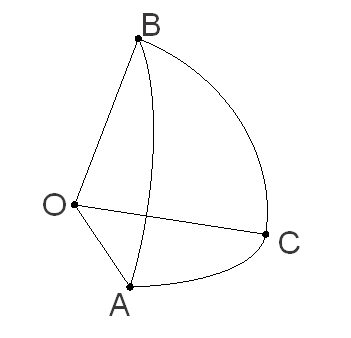
Рисунок 3 – Дополнительные плоскости
Каждая такая плоскость имеет уравнение Ax + By + Cz + D = 0, где А, B, C, D – постоянные, причем А, B и C одновременно не равны нулю. Зная координаты вершин треугольника и точки центра сферы, можно найти коэффициенты плоскостей по формулам 6.
Принадлежность вокселя–претендента сферическому треугольнику определяется его положением относительно трех дополнительных плоскостей. Так, если воксель–претендент принадлежит сферическому треугольнику, то подставив координаты его центра в уравнения всех трех плоскостей, мы получим неотрицательное значение. Если же при подстановке координат центра в уравнения хотя бы одно из значений – отрицательное, значит, рассматриваемый воксель не принадлежит сферическому треугольнику.
На рисунке 4 представлен пример работы алгоритма генерации воксельного разложения сферического треугольника, визуализированный с помощью пакета Mathematica 9.
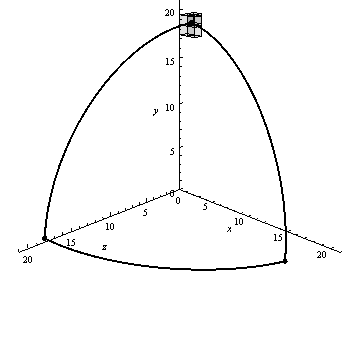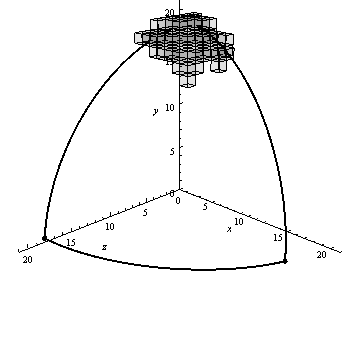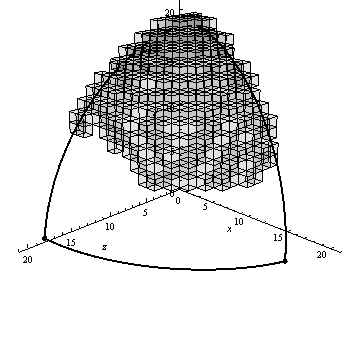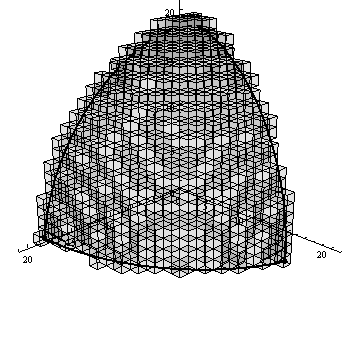
Рисунок 4 – Работа алгоритма вокселизации сферического треугольника (анимация: 13 кадров, 10 циклов повторения, 67.8 кБ)
4.4. Экспериментальные исследования алгоритма воксельного разложения сферического треугольника
Экспериментальное исследование предложенного алгоритма (с проверкой принадлежности точки треугольнику двумя методами) заключалось в генерации 1000 произвольных сферических треугольников в Ω с H = 20. Вершины треугольников генерировались с помощью генератора псевдослучайных чисел. Эксперименты выполнялись на персональном компьютере CPU Intel(R) Core(TM) i5-3317U CPU @ 1.70GHz, 8ГБ ОЗУ. Для измерения времени работы алгоритма в начале и в конце работы программы записывались метки времени. В качестве времени выполнения программы была использована разность начальной и конечной меток, хотя данный показатель нельзя считать абсолютно точным (на практике данный подход дает недостаточно точные результаты). Обобщенные результаты экспериментов приведены в таблице 2.
Таблица 2 – Результаты экспериментального исследования
| Метод проверки площадью | Метод проверки плоскостями | |
|---|---|---|
| Время генерации 1000 треугольников, мс | 261 620 | 226 566 |
| Количество сгенерированных вокселей | 586 090 | 586 090 |
| Среднее время генерации треугольника, мс | 261,62 | 226,56 |
| Среднее время генерации вокселя, мс | 0,446 | 0,387 |
Исходя из данных, приведенных в таблице 2, можно сделать вывод о том, что метод проверки плоскостями в среднем на 15% быстрее метода проверки площадью.
Кроме того, результат эксперимента показывает, что работа метода проверки принадлежности точки сферическому треугольнику с помощью вспомогательных плоскостей оказалась быстрее метода проверки площадью в 96% вариантов треугольников. Это объясняется тем, что для данного метода требуется меньший объем вычислений, т.к. в начале алгоритма производится расчет коэффициентов трех плоскостей, а затем в цикле в найденные уравнения подставляются координаты конкретных точек. Для метода проверки с помощью площадей на начальной этапе возможно лишь вычисление общей площади сферического треугольника, а затем в цикле происходит вычисление площадей трех треугольников, образованных конкретной заданной точкой и вершинами исходного сферического треугольника. Очевидно, что вычисление значения уравнения в точки менее трудоемкий процесс, чем расчет площади сферического треугольника.
Выводы
В работе предложен подход для решения задачи вокселизации сферического треугольника.
В предложенном алгоритме рассмотрены два метода проверки точки на принадлежность сферическому треугольнику и проведен их сравнительный анализ.
Предложенный в работе подход может рассматриваться только как начальный, требующий дополнительных исследований в направлении минимизации количества вокселей в генерируемом разложении и его оптимизации с целью сокращения как временных затрат, так и требуемой памяти.
Дальнейшая работа будет направлена на оптимизацию алгоритма, а также на разработку алгоритмов генерации воксельного разложения для других поверхностей второго порядка.
Список источников
- Томилин М.Г., Невская Г.Е. Дисплеи на жидких кристаллах: Учебное пособие. – СПб: СПбГУ ИТМО, 2010. – c.73.
- Башков Е.А., Авксентьева О.А., Аль-Орайкат Анас М. К построению генератора графических примитивов для трехмерных дисплеев [Текст]. В сб. Наукові праці Донецького національного технічного університету, серія "Проблеми моделювання та автоматизації проектування динамічних систем". Вип. 7 (150). – Донецьк, ДонНТУ. – 2008 .– с. 203–214.
- Kaufman, A., Shimony, E., '3D Scan–Conversion Algorithms for Voxel–Based Graphics', Proc. ACM Workshop on Interactive 3D Graphics, Chapel Hill, NC, October 1986, pp. 45–76.
- S.Wang, A. Kaufman. Volume sampled voxelization of geometric primitives. Proceedings of Visualization’ 1993, pp. 78–84.
- S.Wang, A. Kaufman. Volume–sampled 3D modeling. Computer Graphics and Applications, 1994, pp. 26–32.
- N. Stolte, R. Caubet. Discrete Ray–Tracing of Huge Voxel Spaces Computer Graphics Forum, 1995.
- N. Stolte, R. Caubet. Comparison between different rasterization methods for implicit surfaces. Visualization and Modeling, 1997.
- N. Stolte, A. Kaufman. Parallel spatial enumeration of implicit surfaces using interval arithmetic for octree generation and its direct visualization. Implicit Surfaces', 1998.
- Shiaofen Fang, Hongsheng Chen. Hardware accelerated voxelization. Computers & Graphics, 2000, pp. 433–442.
- Sema Koca, Ulus Cevikb. A new approach for the voxelization of volumetric CSG graphs, 2004, pp. 245–255.
- Катасонов А.В., Вяткин С.И., Долговесов Б.С. Вокселизация функциональных форм [Электронный ресурс]. Режим доступа: http://www.graphicon.ru/html/2005/proceedings/papers/Katasonov_Vyatkin.pdf.
- Башков Е.А., Авксентьева О.А., Аль–Орайкат Анас Махмуд, Хлопов Д.И. Генератор отрезков прямых повышенной производительности для трехмерных дисплеев. В сб. Научные труды ДонНТУ. Серия «Информатика, кибернетика и вычислительная техника». – 2010. – Вып. 11(164). – с. 100–106.
- Коников А.В., Авксентьева О.А. Специализированный процессор для разложения пространственной прямой для объемных 3D дисплеев [Электронный ресурс]. Режим доступа: http://iuskm.donntu.ru/pdf/vol1/Section3.pdf#page=16.
- Харченко Н.О. Структурно–алгоритмическая организация устройств генерации произвольных дуг и секторов в 3D пространстве для объёмных дисплеев [Электронный ресурс]. Режим доступа: http://masters.donntu.ru/2011/fknt/hartchenko/diss/index.htm.
- Башков Е.А., Авксентьева О.А., Половинкин О.А. Базовый алгоритм воксельного разложения пространственного треугольника. В сб. Наукові праці Донецького національного технічного університету. Серiя «Проблеми моделювання та автоматизації проектування» (МАП–2011). Випуск: 10 (197) – Донецьк: ДонНТУ. – 2011. – 290 с.
- Хлопов Д.И. Параллельные методы и алгоритмы построения воксельных моделей в реальном времени [Электронный ресурс]. Режим доступа: http://masters.donntu.ru/2012/fknt/khlopov/diss/index.htm.
- Радченко В.И. Исследование методов анимации воксельных моделей [Электронный ресурс]. Режим доступа: http://masters.donntu.ru/2012/fknt/radchenko/diss/index.htm.
- Большой круг [Электронный ресурс]. Режим доступа: http://ru.wikipedia.org/wiki/Большой_круг
- Сферический треугольник [Электронный ресурс]. Режим доступа: http://ru.wikipedia.org/wiki/Сферический_треугольник
