Abstract
When the abstract was writing this master's work was not complete yet. Final completion: December 2014. Full text of work and materials on the topic can be obtained from the website after this date.
Content
- Introduction
- 1. Theme urgency
- 2. Goal and tasks of the research
- 3. Overview of researches and developments
- 3.1 Overview of international sources
- 3.2 Overview of local sources
- 4. Voxelization algorithm of spherical triangle
- 4.1 Statement of the problem
- 4.2 The basic algorithm of voxel decomposition of a spherical triangle
- 4.3 Checking belonging to the spherical triangle
- 4.4 Experimental researches of voxel decomposition algorithm of spherical triangle
- Conclusion
- References
Introduction
Tendency to create ultra-realistic images makes the creation of volumetric displays relevant. There are a lot of attempts to create a display for displaying three-dimensional objects [1].
3D technologies are advancing rapidly. Two approaches to the construction of display devices were developed: stereoscopic and volumetric. Stereoscopic 3D displays form a separate image for each eye. This principle is used in stereoscopes, known since the beginning of the XIX century. Volumetric displays use different physical phenomena to display points of light within a certain volume.
Creation of such devices require special hardware and software. Feature of display devices based on volumetric technology is the presence of voxel memory – the 3D analogue of memory of the raster display device. When generating a three-dimensional image in voxel memory software creates voxelized
model of real objects, consisting of a combination of 3D graphics primitives: lines segments, surfaces, arcs, circles, spherical triangles, ellipsoids, etc. [2].
1. Theme urgency
Due to the increasing computing power and human interest of the visualization of three-dimensional images, there is a need to develop efficient algorithms for generating graphic primitives, based on which can be built more complex graphic objects and scenes. There are many algorithms for the submission and processing of graphic objects for 2D displays, but 3D devices currently have not uniform standards for representation of graphical information. Algorithms for generating primitives have not been developed too.
Development of new algorithms for generating graphic images in the space of three-dimensional display device is an urgent task that can greatly accelerate the introduction of three-dimensional volumetric display devices in daily life.
2. Goal and tasks of the research
Purpose – development and program implementation of algorithm for generating second order surfaces for 3D volumetric display devices.
To achieve the goal following tasks were set:
- examine existing methods for generating graphic primitives;
- to analyze ways of representing the spherical surface in three-dimensional space and propose an approach for the generation of voxel decomposition of a spherical triangle;
- develop criteria for assessing the accuracy of voxel decomposition;
- develop an algorithm to optimize the number of voxels in the voxel decomposition;
- test the algorithm on different sets of input data;
- test the algorithm on different architectures and platforms with further time-consuming comparison.
3. Overview of researches and developments
Large number of research and development proves the fact that the topic under consideration is popular both in domestic and in the international scientific community.
3.1. Overview of international sources
The first works related with voxelization of geometric primitives appeared in the late 1980s. They represented algorithms based on serial scan of scene [3] (ray tracing). In the early 1990s, American scientists Arie Kaufman and Sidney Wang suggested filtering-antialiasing technology in the works [4,5].
However, for tasks that require accuracy, using smoothing techniques is unacceptable. A new algorithm for generating voxel decomposition was proposed by Nilo Stolte who was involved in the visualization of implicit surfaces in the works [6, 7, 8]. The proposed algorithm is based on recursive partitioning of the space scene using interval arithmetic. The resulting model is represented as an octree. This approach provides greater accuracy, the ability to parallelize and smaller memory footprint, but the performance is still insufficient to use these approaches in interactive applications.
Increased productivity using graphics accelerators was investigated Shiaofen Fang and Hongsheng Chen in [9]. High-performance algorithm for voxelization of solids represented in [10]. This approach is based on a constructive solid geometry that allows you to create a complex scene or object using bit operations to combine several objects. The advantage of this algorithm is that each expression in tree scene can be performed without the use of computing and stacks.
As for russian researches, [11] should be mentioned. It proposes to use a multi-level rays tracking algorithm to visualize models based on the perturbation functions, adapted to tasks of voxelization.
3.2. Overview of local sources
Outside DonNTU researches associated with voxel graphics were not detected.
In university this topic is widespread and is regularly discussed at conferences and in publications. Bashkov E.A., Avksentieva O.A., Anas Al-Mahmoud Oraykat in the paper [2] consider ways to build graphical primitives. In [12] Bashkov E.A., Avksentieva O.A., Al-Oraykat Anas Mahmoud, Khlopov D.I. propose algorithm for generating of line segment.
In the article [13] Konikov A.V., Avksentieva O.A. develop specialized processor for line expansion in the 3D space of the display.
Voxel decomposition algorithm using CUDA arc considered by Master Kharchenko H.O. [14].
In the paper [15] Bashkov E.A., Avksentieva O.A., Polovinkin O.A. describe the algorithm used to generate voxel decomposition of spatial triangle.
Master Khlopov D.I. engaged in parallel algorithms for voxel modeling in real time [16].
Master Radchenko V.I. explored animation techniques for voxel models [17].
4. Voxelization algorithm of spherical triangle
4.1. Statement of the problem
Task of voxel decomposition of a spherical triangle can be stated as follows.
Suppose that a region of three-dimensional Euclidean space that shows in 3D display, has the form of three-dimensional parallelepipedΩ ∈ R3, 0 ≤ x ≤ X, 0 ≤ y ≤ Y, 0 ≤ z ≤ Z. Given the scalability, we assume that X = Y = Z = H, i.e. Ω is cube.
Suppose that Ω is filled with voxels – atomic elements. We define a voxel as a cube, oriented along the axes of Ω, with a single edge. A plurality of voxels filling Ω can be represented as a three-dimensional array of voxels Vi,j,l. Moreover, on the one hand, i, j, l – the indexes of the voxel in the array with values ??0,1, ... H, and on the other, they determine the coordinates of the voxel in Ω. Thus, the voxel Vi,j,l is a subset of Ω, which can be defined as i ≤ x ≤ i + (1-ε), j ≤ y ≤ j + (1-ε), l ≤ z ≤ l + (1-ε), where ε – infinitesimal.
Neighbors of a voxel V(k) with coordinates ik, jk, lk we assume voxels V(g), which satisfy 1.
In further discussions the following function is adopted as the metric.
Let's define coordinates VC of voxel center Vi,j,l as 3.
Assume that the triangle lies on a spherical field Φ centered at the origin with radius R. The triangle formed by the vertices A = [xA, yA, zA], B = [xB, yB, zB], С = [xC, yC, zC], wherein A ≠ B ≠ C and ||A|| = ||B|| = ||C|| = R.
Task of voxel decomposition of a spherical triangle ABC will be understood as finding the set Θ of voxels belonging to the sphere Φ and lying inside a closed compartment of the sphere bounded by segments of great circles [18] AB, BC, CA.
For each voxel V(k) in the expansion given following conditions must be provided:
- length of the perpendicular from the center of V(k) to Φ should not exceed 0,866;
- voxels must lie within the scope of the Φ, Limited by segments of great circles AB, BC, CA;
- number of voxels in the decomposition should be minimal;
- any voxel had at least 8 neighbors.
4.2. The basic algorithm of voxel decomposition of a spherical triangle
Suppose there are peaks A, B, C, describing the spherical triangle. To find the voxel decomposition of such a triangle, you can use the following approach.
The algorithm can be represented in pseudocode as follows:
Input vertices of the triangle А, B, C;
Resulting list of voxels = null;
List of voxels for checking = null;
List of rejected voxels = null;
for(i = 0; i < 3; i++){
Resulting list of voxels.add(Vertices[i]);
List of voxels for checking.add(Vertices[i]);
}
while(List of voxels for checking is not empty){
Current voxel = List of voxels for checking.pop();
Neighbours = Current voxel.getNeighbours();
for(i = 0; i < 26; i++){
if(Neighbours[i] is rejected || Neighbours[i] is in result)
continue;
if(Neighbours[i] is in triangle && Neighbours[i] is on the surface) {
Resulting list of voxels.add(Neighbours[i]);
List of voxels for checking.add(Neighbours[i]);
} else {
List of rejected voxels.add(Neighbours[i]);
}
}
}
Resulting list of voxels.sort by distanse to surface();
foreach(Voxel in Resulting list of voxels){
Voxel.optimizeNeighbours();
}
Output Resulting list of voxels;
It should be noted that in the considered algorithm process of checking whether the point is in spherical triangle has the highest computational complexity. It is important to choose such a method which would minimize hardware costs and time.
4.3. Checking belonging to the spherical triangle
Assume that the q-th voxel decomposition was found. Next voxels are searched among voxels-bidders which metric is not greater than 1. Coordinate increments for voxel-bidders are given in Table 1.
Table 1 – Coordinate increments for voxel-bidders
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| y | -1 | -1 | -1 | 0 | 0 | 0 | 1 | 1 | 1 | -1 | -1 | -1 | 0 | 0 | 1 | 1 | 1 | -1 | -1 | -1 | 0 | 0 | 0 | 1 | 1 | 1 |
| z | -1 | 0 | 1 | -1 | 0 | 1 | -1 | 0 | 1 | -1 | 0 | 1 | -1 | 1 | -1 | 0 | 1 | -1 | 0 | 1 | -1 | 0 | 1 | -1 | 0 | 1 |
When 26 voxels are found we need to choose those which potentially belong to the result set of voxels. To find such voxels one of the following approaches can be used.
1. Checking belonging to the spherical triangle by area
We need to check whether a point P inside spherical triangle ABC. The position of point P in the triangle shown in figure 1.
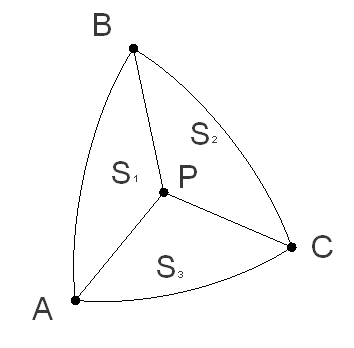
Figure 1 – Position of point P in the triangle
Need to build three triangles lying on the surface of a sphere: ABP, BCP, ACP and calculate the area of ??these triangles: S1, S2 and S3 accordingly. If the point P lies in the triangle ABC, the sum of areas of ABP, BCP, APC(S1 + S2 + S3) is equal to SABC.
Formula 4 is used to find the area of ??each spherical triangle.
In formula α, β, γ – angles of a spherical triangle [19]. The angles of the spherical triangle are shown in figure 2.
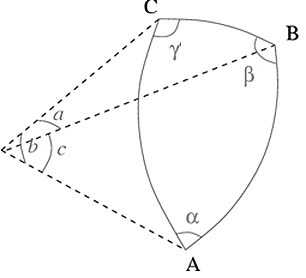
Figure 2 – Angles and sides of a spherical triangle
On figure 2 a, b, c – sides of a spherical triangle [19]. Angles of a spherical triangle are calculated according to the formulas 5.
Side of a spherical triangle are found by calculating the angles formed by the vector from the center of the sphere to the vertices of a spherical triangle.
2. Checking belonging to the spherical triangle by planes
Among the candidates need to select those centers of which are located between the three planes. Each of these planes is formed by one side of the spherical triangle and the center point of the sphere. So, it is necessary to construct an additional planes AOB, BOC, COA, as shown in figure 3.
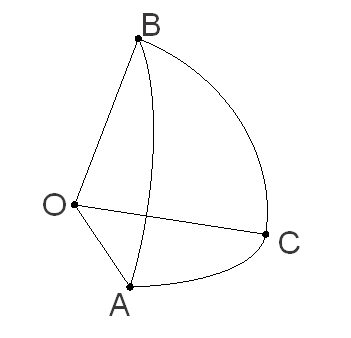
Figure 3 – Additional planes
Each plane has the equation Ax + By + Cz + D = 0, where А, B, C, D – are constants. А, B and C are not zero at the same time. Knowing the coordinates of the vertices of the triangle and the center point of the sphere, we can find the coefficients of the planes using formulas 6.
Belonging of the point to spherical triangle is defined by position of point relative to three additional planes. If voxel belongs spherical triangle, then substituting the coordinates of its center in all three equation of the planes, we obtain a non-negative value.
Figure 4 shows an example of the algorithm generating voxel decomposition of the spherical triangle visualized using Mathematica 9.
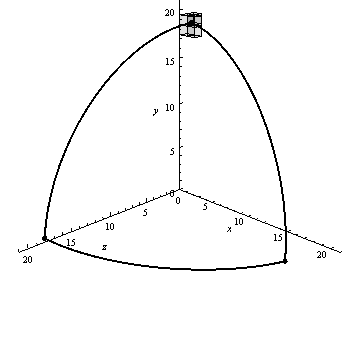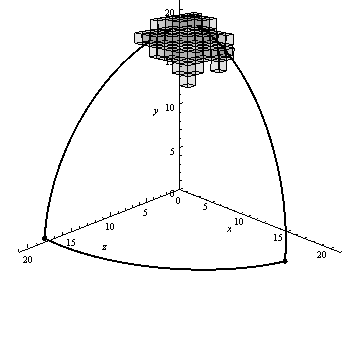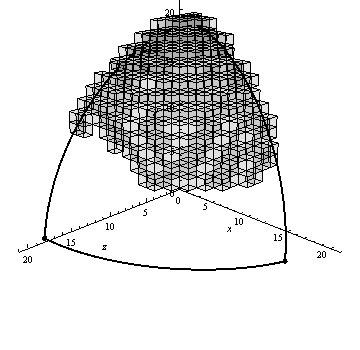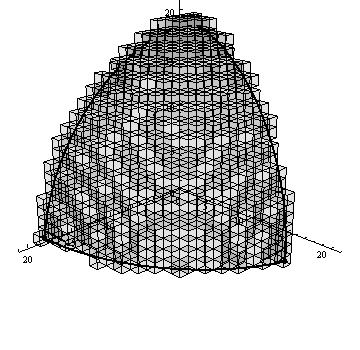
Figure 4 – Algorithm generating voxel decomposition of spherical triangle (animation: 13 shots, 10 cycles, 67.8 kB)
4.4. Experimental researches of voxel decomposition algorithm of spherical triangle
Experimental research of the proposed algorithm (with checking point belonging to the triangle in two ways) was to generate 1,000 random spherical triangles in Ω with H = 20. Vertices of triangles were generated using a random number generator. The experiments were performed on a personal computer CPU Intel (R) Core (TM) i5-3317U CPU@1.70GHz, 8GB RAM. To measure the running time at the beginning and end of the program timestamps were recorded. Difference of initial and final timespamps was used as the execution time of the program. Summarized results of the experiments are shown in table 2.
Table 2 – Results of experiment
| Checking belonging to the spherical triangle by areas | Checking belonging to the spherical triangle by planes | |
|---|---|---|
| Time of generating 1000 of triangles, ms | 261,620 | 226,566 |
| Total amount of voxels | 586,090 | 586,090 |
| Average time of generating of a triangle, ms | 261.62 | 226.56 |
| Average time of generating of a voxel, ms | 0.446 | 0.387 |
Based on the data presented in table 2, it can be concluded that the method of checking by planes on average 15% faster than the area method.
Furthermore, the experimental result indicates that the method using the auxiliary planes was faster in 96% of the triangles. Obviously, the calculation of the equation in point is much less computationally expensive than calculating the area of a spherical triangle.
Conclusion
This paper proposes an approach for solving the problem of spherical triangle voxelization.
In the proposed algorithm considered two methods of checking points on the spherical triangle belonging and their comparative analysis.
The proposed approach can only be considered as an initial requiring further research in the direction of minimizing the number of voxels in the generated expansion and optimization in order to reduce both time-consuming and required memory.
Further work will be aimed at optimizing the algorithm and to develop algorithms for generating voxel expansions for other quadrics.
References
- Томилин М.Г., Невская Г.Е. Дисплеи на жидких кристаллах: Учебное пособие. – СПб: СПбГУ ИТМО, 2010. – c.73.
- Башков Е.А., Авксентьева О.А., Аль-Орайкат Анас М. К построению генератора графических примитивов для трехмерных дисплеев [Текст]. В сб. Наукові праці Донецького національного технічного університету, серія "Проблеми моделювання та автоматизації проектування динамічних систем". Вип. 7 (150). – Донецьк, ДонНТУ. – 2008 .– с. 203–214.
- Kaufman, A., Shimony, E., '3D Scan–Conversion Algorithms for Voxel–Based Graphics', Proc. ACM Workshop on Interactive 3D Graphics, Chapel Hill, NC, October 1986, pp. 45–76.
- S.Wang, A. Kaufman. Volume sampled voxelization of geometric primitives. Proceedings of Visualization’ 1993, pp. 78–84.
- S.Wang, A. Kaufman. Volume–sampled 3D modeling. Computer Graphics and Applications, 1994, pp. 26–32.
- N. Stolte, R. Caubet. Discrete Ray–Tracing of Huge Voxel Spaces Computer Graphics Forum, 1995.
- N. Stolte, R. Caubet. Comparison between different rasterization methods for implicit surfaces. Visualization and Modeling, 1997.
- N. Stolte, A. Kaufman. Parallel spatial enumeration of implicit surfaces using interval arithmetic for octree generation and its direct visualization. Implicit Surfaces', 1998.
- Shiaofen Fang, Hongsheng Chen. Hardware accelerated voxelization. Computers & Graphics, 2000, pp. 433–442.
- Sema Koca, Ulus Cevikb. A new approach for the voxelization of volumetric CSG graphs, 2004, pp. 245–255.
- Катасонов А.В., Вяткин С.И., Долговесов Б.С. Вокселизация функциональных форм [Электронный ресурс]. Режим доступа: http://www.graphicon.ru/html/2005/proceedings/papers/Katasonov_Vyatkin.pdf.
- Башков Е.А., Авксентьева О.А., Аль–Орайкат Анас Махмуд, Хлопов Д.И. Генератор отрезков прямых повышенной производительности для трехмерных дисплеев. В сб. Научные труды ДонНТУ. Серия «Информатика, кибернетика и вычислительная техника». – 2010. – Вып. 11(164). – с. 100–106.
- Коников А.В., Авксентьева О.А. Специализированный процессор для разложения пространственной прямой для объемных 3D дисплеев [Электронный ресурс]. Режим доступа: http://iuskm.donntu.ru/pdf/vol1/Section3.pdf#page=16.
- Харченко Н.О. Структурно–алгоритмическая организация устройств генерации произвольных дуг и секторов в 3D пространстве для объёмных дисплеев [Электронный ресурс]. Режим доступа: http://masters.donntu.ru/2011/fknt/hartchenko/diss/index.htm.
- Башков Е.А., Авксентьева О.А., Половинкин О.А. Базовый алгоритм воксельного разложения пространственного треугольника. В сб. Наукові праці Донецького національного технічного університету. Серiя «Проблеми моделювання та автоматизації проектування» (МАП–2011). Випуск: 10 (197) – Донецьк: ДонНТУ. – 2011. – 290 с.
- Хлопов Д.И. Параллельные методы и алгоритмы построения воксельных моделей в реальном времени [Электронный ресурс]. Режим доступа: http://masters.donntu.ru/2012/fknt/khlopov/diss/index.htm.
- Радченко В.И. Исследование методов анимации воксельных моделей [Электронный ресурс]. Режим доступа: http://masters.donntu.ru/2012/fknt/radchenko/diss/index.htm.
- Большой круг [Электронный ресурс]. Режим доступа: http://ru.wikipedia.org/wiki/Большой_круг
- Сферический треугольник [Электронный ресурс]. Режим доступа: http://ru.wikipedia.org/wiki/Сферический_треугольник
