|
Для сокращения времени поиска численного решения исходной задачи Коши вида (4.1) могут быть использованы
методы с более высокой скоростью сходимостью, чем исходный итерационный.
Суть метода Ньютона состоит в поиске очередного приближения по формуле (6.1). Величина
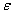 определяет поправку
для получения искомого численного решения на очередной итерации [5].
определяет поправку
для получения искомого численного решения на очередной итерации [5].
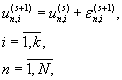 (6.1) (6.1)
Система линейных уравнений, связывающая поправки
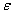 n,i
(0 < i < k+1) и численные решения un,i (0 < i < k+1) текущей
итерации s имеет вид (6.2). В качестве искомых неизвестных выступают поправки n,i
(0 < i < k+1) и численные решения un,i (0 < i < k+1) текущей
итерации s имеет вид (6.2). В качестве искомых неизвестных выступают поправки
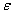 n,i
(0 < i < k+1). n,i
(0 < i < k+1).
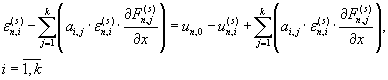 (6.2) (6.2)
Использование метода Ньютона в одношаговом многоточечном методе (для определения значений поправок
на каждой итерации) требует решения СЛАУ. Каждый метод решения систем уравнений (прямой или итерационный)
предполагает определённое отображение исходных и промежуточных данных на узлы вычислительной сети.
Следовательно, время выполнения алгоритма решения задачи Коши, заданного формулами (6.1) – (6.2), в целом
будет определяться выбранным алгоритмом решения СЛАУ. Дополнительно следует учесть время выполнения
возможных коммуникационных и вычислительных операций, обеспечивающих подготовку и отображение необходимых
для использования алгоритма решения СЛАУ данных.
|