|
Для систем из m ОДУ разностные уравнения типа (4.2) принимают вид в соответствии с формулой (7.1). Формула
предполагает связь рассчитываемых величин с блоком n.
 (7.1) (7.1)
По аналогии с формулировкой задачи Коши вида (4.1), для системы уравнений подразумеваются следующие
факты [5]:
- задание начальных значений u0,j для блока n = 1;
- для блоков n > 1 начальные условия u0,j вычисляются в предыдущем блоке (n – 1).
Для решения системы используется итерационный процесс вида (7.2) для предварительной стадии и
(7.3) непосредственно для самих итераций поиска решения [5].
 (7.2) (7.2)
 (7.3) (7.3)
Пусть численный расчёт значений искомой функции осуществляется на k вычислительных узлах. Пусть
узел с номером i осуществляет расчёт значений
 в фиксированной точке ti по всем уравнениям. Для реализации расчётов на узле необходимо
наличие следующих данных:
в фиксированной точке ti по всем уравнениям. Для реализации расчётов на узле необходимо
наличие следующих данных:
- вектор начальных приближений искомой функции
 ; ;
- вектор значений ОДУ для сеточных функций в нулевом узле блока
 ; ;
- значение элемента bi вектора B коэффициентов разностной одношаговой
многоточечной схемы;
- вектор значений элементов
 , который является i–ым столбцом матрицы A;
, который является i–ым столбцом матрицы A;
- вектор значений элементов
 , который является i–ой строкой матрицы F.
, который является i–ой строкой матрицы F.
Рисунок 7.1 представляет вычислительную зависимость элементов
 матрицы U(s+1) на (s+1)–ой итерации расчётов.
матрицы U(s+1) на (s+1)–ой итерации расчётов.
Рисунок 7.1 – Вычислительная зависимость элементов
 матрицы U(s+1)
матрицы U(s+1)
Особенность такого метода осуществления расчётов – необходимость вычисления всех k * m значений
матрицы F(s). Данный вычислительный узел i содержит только i–ую строку матрицы
F(s).
Пусть все вычислительные узлы в соответствии с их номерами объединены в кольцо (см. рисунок 7.2).
Как было описано выше, узел i содержит i–ую строку матрицы F(s). Элементы других строк
могут быть получены путём выполнения коммуникационной операции их циклического сдвига между
узлами кольца (m–1) раз на расстояние единичной длины. Каждый раз после выполнения такого сдвига
соответствующие вычислительные узлы будут получать необходимые для вычисления данные.
Разные стадии операции циклического сдвига представлены на рисунке 7.2.
Рисунок 7.2 – Стадии выполнения серии операций циклического сдвига
Время решения системы ОДУ по всем n блокам без учёта коммуникационных затрат определяется формулой
(7.4). Время расчёта значения функции
 определяется значением функции
определяется значением функции
![Tf[delta]](../images/diss/temp7o7.gif) , где
, где
 – длительность модельного такта времени (обозначение введено в связи с другим смыслом величины
– длительность модельного такта времени (обозначение введено в связи с другим смыслом величины
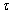 ). ).
 (7.4) (7.4)
Ускорение параллельного алгоритма решения системы ОДУ блочным одношаговым методом c учётом времени
выполнения коммуникационных операций формула ускорения принимает вид (7.5).
 (7.5) (7.5)
Рисунки 7.3 и 7.4 представляют соотношения времён выполнения последовательного и параллельного
алгоритмов с учётом коммуникационных затрат. Рисунки представляют зависимость времени выполнения
параллельного алгоритма от числа уравнений и числа точек внутри блока соответственно. Величина
ускорения не зависит от числа блоков.
Рисунок 7.3 – Зависимость ускорения параллельного алгоритма с учётом коммуникационных затрат
от количества уравнений
Рисунок 7.4 – Зависимость ускорения параллельного алгоритма с учётом коммуникационных затрат
от количества точек внутри блока
Эффективность использования процессоров вычислительных узлов параллельным алгоритмом решения
системы ОДУ блочным одношаговым методом c учётом времени выполнения коммуникационных операций
формула эффективности принимает вид (7.6).
 (7.6) (7.6)
Рисунки 7.5 и 7.6 представляют соотношения времён выполнения последовательного и параллельного
алгоритмов с учётом коммуникационных затрат. Рисунки представляют зависимость времени выполнения
параллельного алгоритма от числа уравнений и числа точек внутри блока соответственно. Величина
эффективности не зависит от числа блоков.
Рисунок 7.5 – Зависимость эффективности параллельного алгоритма с учётом коммуникационных затрат
от количества уравнений
Рисунок 7.6 – Зависимость эффективности параллельного алгоритма с учётом коммуникационных затрат
от количества точек внутри блока
|