|
Задача Коши для обыкновенного дифференциального уравнения 1–ого порядка имеет вид, заданный
формулой (4.1).
 (4.1)
Для численного решения задачи Коши необходимо вычислить множество значений искомой функции
на заданном интервале. Бесконечное множество точек интервала заменяется конечным. Значения
искомой функции восстанавливается в узлах сетки, которая заменяет исходный интервал. Узлы сетки
равно удалены друг от друга на величину задаваемого шага. Приближённое решение находится с заданной
точностью, которая определяется частотой узлов сетки и особенностями численного метода поиска
решения [5].
Пусть множество M точек равномерной сетки {tm}, m = 1, M и tm = T c шагом
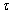разбивается на N блоков, содержащих по k точек каждый. При этом суммарное число точек по всем
блокам кратно общему количеству блоков.
Пусть n – номер (индекс) блока сетки, i – номер (индекс) точки в рамках блока и tn, i – точка с
номером i в блоке с номером n. Характерные точки блока n:
- tn, 0начальная точка блока, не включаемая в него;
- tn, kконечная точка блока.
-
Схема разбиения на блоки для одношагового k–точечного метода представлена на рисунке 4.1.
Рисунок 4.1 – Схема разбиения на блоки для одношагового k–точечного метода
Главная особенность одношагового блочного метода состоит в том, что новые k значений искомой функции
вычисляются одновременно. Такая вычислительная независимость позволяет осуществлять расчёт
искомого решения в точках блока одновременно [5].
Уравнения многошаговых разностных методов для блока из k точек при использовании вычисленных значений
приближённого решения в m предшествующих блоку узлах имеют вид (4.2). Данная формула определяет
одношаговый k–точечный метод [5].
 (4.2)
|
