В современной цитологии для решения диагностических и лечебных задач необходима оценка комплекса параметров клеток. Одним из вопросов, ответ на который может позволить повысить эффективность диагностики и лечения, является прогнозирование параметров процесса прикрепления, в частности, нейтрофилов, без чего они не в состоянии выполнять свойственные им функции. К сожалению, работы начатые в этом направлении [1 – 3] не развивались в последнее десятилетие. В то же время получение оцифрованных изображений проекций клеток и расчет их геометрических параметров не представляет технических трудностей.
Целью магистерской работы является разработка специализированной компьютерной системы (СКС), которая будет прогнозировать параметры процесса прикрепления клеток крови, на примере нейтрофилов. Входной информацией являются геометрические параметры клеток, в частности, периметр (P), площадь (S), компактность (C = P 2/S), набор моментов первого (F1), второго (F2) и третьего (F3) порядков, разность (F3-F1), а также интеграл множества нормированных дескрипторов Фурье (FF). На выходе будут представлены спрогнозированные геометрические параметры клеток в указанный момент времени и предполагаемый результат процесса прикрепления.
У добровольцев производили забор 1 мл капиллярной крови, гепаринизовали и отстаивали 40 мин при температуре 37° С. После производили отбор суспензии лейкоцитов, содержащую нейтрофилы и анализировали под микроскопом (Люмам-Р3, х90). Исследовали процесс прикрепления нейтрофилов во времени (t). Снимки проекций клеток производились каждые 3 мин цифровой видеокамерой CCD Oscar Color Camera OS-35II. На рис.1 представлена блок-схема СКС.

Рисунок 1 - Блок-схема СКС для измерения параметров клетки в процессе прикрепления.
Изображения нейтрофилов получали с помощью программы ASUS Live Version 4.6 B2 (см. рис.2).

Рисунок 2 – Изображения нейтрофилов в поле зрения микроскопа (стрелкой показан прикрепляющийся нейтрофил).
Поученные изображения нейтрофилов обрабатывали в специально написанной программе [4]. В обработку входило оконтуривание проекции клетки и автоматический расчет геометрических параметров.
На рисунке 3 представлен процесс прикрепления нейтрофила (увеличение периметра) и контур клетки, полученный по окончанию процесса.
 |
(анимация повторяется циклически 5 раз,
для повторного запуска - обновить страницу,
размер 117 Кб, количество кадров - 4,
использовалась программа MP Gif Animator ) |
Рисунок 3 - Процесс прикрепления нейтрофила.
Выделение контура нейтрофила производилось с помощью манипулятора «мышь» в разные моменты времени, контур представлен матрицей точек (x i; yi). Для каждого изображения нейтрофилов выделение контура проводили 10 раз, определяли среднее значение и доверительный интервал с доверительной вероятностью 0,95.
Ниже приведены формулы, которые использовались при расчете геометрических параметров клетки, помимо площади и периметра.
Компактность:
 ,
,
где P - это длина периметра области; S - площадь области.
Границы области или объекта характеризуются упорядоченной последовательностью, которая представлена Евклидовыми расстояниями между центром области и всеми пикселями контура оцифрованного объекта. Моменты являются безразмерными величинами, что позволяет использовать прямое или комбинированное сравнение. Чем больше значение, тем более шероховатый контур фигуры. Набор моментов первого, второго и третьего порядков являются характеристиками формы объекта и не зависят от аффинных преобразований, они вычисляются по формулам:



где  - p-й момент,
- p-й момент,
 - p-й главный центральный момент,
- p-й главный центральный момент,
zi - расстояния от геометрического центра объекта до i-й точки контура.
N – количество точек в обрабатываемом контуре.
Дескриптор Фурье является характеристикой формы и рассчитывается по множеству нормированных дескрипторов Фурье (формула приведена ниже).

Где NFD(k) – нормированные дескрипторы Фурье, которые не зависят от местоположения и размера контура, а также от положения начальной точки и направления обхода:

.jpg)
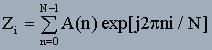
При расчете геометрических характеристик использовался доверительный интервал с доверительной вероятностью 0,95. В медицинских исследованиях, в качестве доверительных, используют следующие погори вероятностей: p=0,95; p=0,99; p=0,999.
Интервальной называют оценку, которая определяется двумя числами – концами интервала и покрывает оценочный параметр.
Доверительным называют интервал, который с заданной надежностью  покрывает заданный параметр.
покрывает заданный параметр.
Интервальной оценкой (с надежностью  ) математического ожидания а нормально распределенной количественной характеристики
) математического ожидания а нормально распределенной количественной характеристики 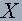 по выборочному среднему
по выборочному среднему  при известном среднеквадратическом отклонении служит доверительный интервал:
при известном среднеквадратическом отклонении служит доверительный интервал:


где, 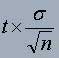 - точность оценки,
- точность оценки,
N – объем выборки,
 - среднеквадратическое отклонение,
- среднеквадратическое отклонение,
t – значение аргумента функции Лапласа Ф(t), при котором Ф(t) = 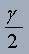
В свою очередь  рассчитывается по формуле:
рассчитывается по формуле:

Где Xi - элемент выборки
Кинетическая модель – модель, которая описывает поведение компонентов системы во времени. Переменными в таких моделях являются обычно концентрации и геометрические размеры компонентов системы.
Вид зависимостей P и S позволил предположить, что их можно описать кинетическим уравнением первого порядка:

где c – P или S в момент времени t;
b – P0 или S0 – соответственно P или S при t = 0;
a – (P - P0) или (S
- P0) или (S - S0) - P
- S0) - P , S
, S - соотвественно P, S при
- соотвественно P, S при  ;
;
k – константа скорости, c-1.
Это допущение было сделано на основании внешнего вида зависимостей периметра и площади от времени (см. рис. 4):

Рисунок 4 - Кинетическая модель изменения геометрических параметров нейтрофила с течением времени: P (1), S (2), C (3).
Как видно из рисунка значение P и S увеличиваются с течением времени, за исключением компактности, которая с течением времени в пределах погрешности остается постоянной.
Вид зависимостей F1, F2, F3, (F3 - F1) и FF от времени (рисунок 5) свидетельствует о том, что в случае этих характеристик имеет место более сложная зависимость, чем выше описанное уравнение первого порядка. Поэтому построение кинетической модели для моментов F1, F2, F3 невозможно без дополнительной обработки выходных данных.

Рисунок 5 - Изменение моментов F1, F2, F3 и разности F3 - F1 во времени в процессе прикрепления.
Таким образом, зная кинетическую модель процесса и входные данные, СКС сможет прогнозировать параметры процесса прикрепления и степень его завершенности в любой указанный момент времени, что позволит сократить временные затраты на 75-80%.
Ниже представлены ссылки на работы магистров ДонНТУ, в которых рассмотрены схожие вопросы.
1. Оценка функционального состояния нейтрофилов на основе анализа изображений. Баева Д. Н. (http://masters.donntu.ru/2005/kita/bayeva/diss/index.htm)
2. Построение автоматизированной системы определения контура объекта на примере изображения клеток. Трибрат А.А. (http://masters.donntu.ru/2005/kita/tribrat/diss/index.htm)
3. Разработка экспертной системы определения биологического состояния клеток, построенной на энтропийных методах. Евстратов А.Н. (http://masters.donntu.ru/2004/kita/evstratov/diss/diss.html)
4. Разработка специализированной компьютерной системы определения стадий апоптоза посредством оболочки Clips. Прываев А.М. (http://masters.donntu.ru/2002/kita/porivaev/diss/diss.htm)
5. Разработка экспертной системы определения биологического состояния клеток, построеноой на энтропийных методах. Коков А.А. (http://www.masters.donntu.ru/2003/kita/kokov/index.htm)
6. Разработка методов и алгоритмов оценки функционального состояния клеток. Каира В.В (http://www.masters.donntu.ru/2005/kita/kaira/index.htm)
Ниже приведены ссылки на сайты мировых организаций, которые занимаются вопросами исследования жизнедеятельности клеток.
1. Государственный Научный Центр Вирусологии и Биотехнологии ВЕКТОР. Изучение клеток крови. (http://www.ntmdt.ru/Application-Notes/Science_Technology_Applications/Life_Sciences/Blood_cells_study/text93.html)
2. БелГУ. Научно-исследовательская лаборатория «Физиология клеток крови» (http://www.bsu.edu.ru/struktura/Centers/NILFizKlKr)
1. Процесс прикрепления нейтрофилов крови человека in vitro описан кинетическим уравнением первого порядка. Найдены параметры уравнения и рассчитано время завершения процесса прикрепления.
2. Компьютерная система позволит уменьшить время исследования до 10 – 15%, от общего времени, для оценки степени завершенности процесса прикрепления нейтрофилов.
1. Медовый В. С., Балабуткин В. А., Верденская Н. В., Гусев А. А., Иванова И. А., Козинец Г. И., Погорелов В. М., Пятницкий А. М., Стоянов М. С., Соколинский Б. З., Теохаров А. Н. Автоматизированные цитофотометрические тесты мазков крови для общей клиники и скрининговых обследований населения // Клин. лаб. диагн.. – 1997. – N 10. – С. 6 – 8
2. Погорелов В. М., Медовый В. С., Хазем Г. М., Козинец Г. И. Анализ клеточного изображения // Клин. лаб. диагн. – 1995. – N 3. – С. 40 – 43
3. Погорелов В. М., Медовый В. С., Балабуткин В. А., Соколинский Б. З., Пятницкиий А. М., Козинец Г. И. Методы компьютерной цитологии в гематологических исследованиях // Клин. лаб. диагн. – 1997. – N 11. – С. 40 – 42
4. Меркулова Е. В., Трибрат А. А., Герасимов И. Г. Оценка функционального состояния клеток с использованием методов цифровой обработки изображений // Наук. праці Донецького нац. техніч. унів. Сер.: Обчислювальна техніка та автоматизація. – Вип. 106. – Донецьк: ДонНТУ, 2006. – С. 145 – 149
5. Grenander U. Geometrics of Knowledge // Proc. Natl. Acad. Sci. USA. – 1994. – N 3. – P. 783 – 789
6. Курский М. Д., Костерин С. А., Рыбальченко В. К. Биохимическая кинетика. – Киев: Вища школа, 1977. – 264 с
7. Кузнецов С. Л., Пугачев М. К. Лекции по гистологии, цитологии и эмбриологии. – М.: Мед. информ. агенство, 2004. – 432 с
8. Shen L., Rangayyan R. M., Desautels J. E. L. Application of Shape Snalysis to Mammographic Calcifications // IEEE Trans. Med. Imag. – 1994. – V. 13, N 2. – P. 263 – 274




 ,
,



 - p-й момент,
- p-й момент, - p-й главный центральный момент,
- p-й главный центральный момент, 

.jpg)
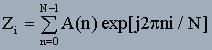
 покрывает заданный параметр.
покрывает заданный параметр.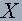 по выборочному среднему
по выборочному среднему  при известном среднеквадратическом отклонении служит доверительный интервал:
при известном среднеквадратическом отклонении служит доверительный интервал: 

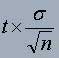 - точность оценки,
- точность оценки, - среднеквадратическое отклонение,
- среднеквадратическое отклонение,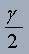


 - P0) или (S
- P0) или (S ;
;
