Автореферат

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность. В настоящее время происходит автоматизация процессов во всех сферах знаний окружающего мира. В некоторых сферах применения эта автоматизация сводится к созданию программного обеспечения для персонального компьютера, но в большинстве случаев требует создания специализированных ЭВМ. Для организации работы ЭВМ необходим управляющий автомат, как одна из составляющих. К его функциям относятся формирование управляющих сигналов, на основе некоторого алгоритма для операционной части ЭВМ.

Эффективность управляющего автомата во многом определяет характеристики системы в целом. Алгоритм управления системы задаётся кодом управления, который поступает в управляющий автомат из внешней среды. Алгоритм управления операционного автомата называется микропрограммой и реализуется управляющим автоматом. Одной из основных проблем при создании специализированной ЭВМ является поиск компромисса между быстродействием, стоимостью и универсальностью управляющего автомата. Также важным является время проектирования и реализации схемы управляющего автомата.

Как известно, УА с жёсткой логикой выигрывают по быстродействию перед автоматами с программированной логикой, но имеют жёсткую структуру и не могут быть измененными. ПЛИС позволяют заменить всё устройство, конфигурированное на микросхему. Таким образом, есть возможность создавать перепрограммированный УА с жёсткой логикой [1].

Конечный автомат представляет собой наиболее общую математическую модель цифрового устройства или цифровой системы. Поэтому очень важно при разработке различных цифровых устройств и систем применять эффективные методы синтеза конечных автоматов. В то же время, реализованные в известных пакетах автоматизированного проектирования (фирм Altera, Xilinx и других) методы синтеза основаны на традиционных подходах, которые не позволяют эффективно использовать архитектурные возможности новой элементной базы.

Традиционно синтез управляющего автомата выполняется по заданной базовой структуре, а оптимизация схемы достигается за счет ряда методов, таких как оптимальное кодирование состояний, выделение подуровней в комбинационных схемах и трансформация кодов объектов. В то же время в операционном автомате ветви алгоритма могут реализовываться параллельно для достижения максимального быстродействия ОА. При традиционной реализации управляющего автомата Мура управление таким ОА должно осуществляться несколькими управляющими автоматами по иерархическому принципу. Что в свою очередь уменьшает быстродействие управляющего автомата за счет увеличения объема последовательной КЛС.

Весомый вклад в научные достижения, относящиеся к проектированию управляющих автоматов, внесли такие ученые как В.М. Глушков, С.И. Баранов, О.О. Баркалов, В.А. Скляров, О.В. Палагин, Г.И. Новиков.

Связь работы с научными программами, планами, темами.

Магистерская работа выполняется в 2008 году соответственно научному направлению кафедры “Электронные вычислительные машины” Донецкого национального технического университета.

Цель исследования – увеличение производительности операционного устройства за счет организации параллельной работы управляющего автомата.

Цель достигается путем решения таких задач исследования:

1. Распараллеливание алгоритма управления.
2. Уменьшение объема последовательной КЛС.
3. Разработка структуры и принципов работы параллельного управляющего автомата с жёсткой логикой на базе FPGA.

Объект исследования – параллельный управляющий автомат на базе сети Петри.

Предмет исследования – схема переходов параллельного управляющего автомата.

Методы исследования представлены аппаратами булевой алгебры, теории множеств и графов, теории сетей Петри и языками описания аппаратуры.

Научная новизна полученных результатов:

• предложена новая структура УА Мура на базе сети Петри с несколькими параллельными состояниями;
• разработан метод синтеза предложенной структуры.

Практическое значение полученных результатов:

• реализация УА Мура на базе сети Петри наиболее оптимально реализуется на ПЛИС с архитектурой FPGA, что приводит к выгодной оптимизации ресурсов ПЛИС;
• предложенный метод синтеза УА Мура позволяет легко автоматизировать процесс синтеза;
• распараллеливание алгоритмов вычисления повышает производительность системы в целом.

ОСНОВНОЕ СОДЕРЖАНИЕ РАБОТЫ

Введение содержит обоснование актуальности решаемой научной задачи, формулирование цели, объекта и задач исследования, совокупность научных результатов, выносимых на защиту, сведения об их апробации.

Первый раздел. Появление в 1978 году простейшей программируемой логической интегральной схемы (ПЛИС) фирмы Monolithic Memories, позволившей реконфигурировать разрабатываемое устройство без повторного проектирования печатной платы, серьезно повлияло на структуру рынка полупроводниковых приборов. Сейчас производители предлагают множество разнообразных ПЛИС: программируемые простые, матричные и сложные логические устройства (SPLD, PAL, CPLD), а также программируемые пользователем базовые матричные микросхемы (FPGA) со специфическими характеристиками и сочетанием таких параметров, как быстродействие, энергопотребление, уровень интеграции и стоимость.

В настоящее время в качестве функционального базиса для реализации цифровых схем используются, в основном, FPGA. Сегодня микросхемы с FPGA-архитектурой стремятся "перехватить инициативу" на рынке у структурированных ASIC, предоставляя разработчикам требуемые устройства с высокими плотностью размещения элементов и быстродействием, низкими энергопотреблением и удельной стоимостью в пересчете на вентиль.

Основной программируемый ресурс микросхем с архитектурой FPGA – так называемая логическая ячейка. В ее состав входят генератор логических функций, или конфигурируемый логический блок (КЛБ, CLB), работа которого задается таблицей истинности (Look-Up Table – LUT), триггер и некоторое число специализированных ресурсов, облегчающих реализацию типичных для цифровой схемотехники узлов. Логические ячейки образуют прямоугольную матрицу, окруженную блоками ввода-вывода IOB, обеспечивающими подключение внутренних линий к внешним выводам корпуса ПЛИС.

Традиционно синтез УА выполняется по базовой структуре, например, для УА Мура классическая структура приведена на рис. 1.

Рисунок 1 - Базовая структура УА Мура

При унитарном кодировании состояний УА Мура дешифратор не требуется, что в свою очередь приводит к упрощению системы функций возбуждения регистра Рг.

В состав каждого КЛБ входит D-триггер, что позволяет наиболее оптимально реализовывать на FPGA схемы с древовидной структурой и большим числом состояний, в частности, сети Петри. Автомат Мура с унитарным кодированием состояний можно представить в виде сети Петри, что позволит исключить традиционный синтез автомата по ПСТ.

Модель сети Петри является принципиально асинхронной и служит для отображения и анализа причинно-следственных связей в системе. Для привязки к определенным моментам времени тех или иных переходов используются события.

Простой сетью Петри называется набор N=(S,T,M,P,F), где:

1. S = {s₁, …, s_N} – множество мест;
2. T = {t₁, …, t_N} – множество переходов таких, что S ∩ T = 0;
3. M = {m₁, …, m_N} – множество меток;
4. P = {p₁, …, p_N} – множество событий;
5. F ⊆ μS×T×μS – отношение инцидентности такое, что
   а) ∀(S'₁, t₁, S"₁), (S'₂, t₂, S"₂) ∈ F : (S'₁, t₁, S"₁) ≠ (S'₂, t₂, S"₂) ⇒ t₁ ≠ t₂;
   б) {t| <S', t, S"> ∈ F} = T.

Условия в пункте 5 говорят, что для каждого перехода t ∈ T существует единственный элемент <S', t, S"> ∈ F, задающий для него входное множество мест S' и выходное множество S".

Сеть Петри имеет наглядную форму представления в виде графа, который включает четыре базовых элемента: позиции (места), переходы, дуги и метки. На рис. 2 приведен пример такого графа.

Функционирование сети заключается в перемещении меток m₁-m₃ по дугам между местами S₁-S₃ и формировании событий. Переходы t₁-t₂ задают условия перемещений меток из мест S₁ и S₃. Исходное размещение меток по местам является начальным условием и может быть произвольным [2].

Исходя из этого, произвольная граф-схема алгоритма (ГСА) для УА, является частным случаем сети Петри с одной меткой, которая соответствует текущему состоянию автомата. Множество мест S соответствует множеству состояний автомата, множество переходов t – множеству условных вершин, множество событий – множеству наборов управляющих сигналов.

Таким образом, произвольный УА может быть представлен в виде сети Петри. В том случае, если события возникают по наличию метки в определенном месте, сеть отображает поведение УА Мура. Если события формируются во время перемещений меток между местами, в зависимости от переходов, то сеть отображает поведение автомата Мили.

Данная схема реализуется на FPGA одним из известных методов.

Преимуществом такой реализации УА на FPGA являются:

1. Идентичность блоков и регулярность структуры автомата.
2. Минимальная комбинационная часть, распределенная по всей схеме FPGA.
3. Небольшое число входов комбинационных схем, не зависящее от числа состояний автомата.
4. Высокое быстродействие автомата.
5. Отсутствие традиционного синтеза.

К недостатку метода следует отнести то, что число состояний автомата не может превышать число триггеров заданной микросхемы FPGA, что зачастую соответствует числу КЛБ.

Второй раздел.

Предполагается применить унитарное кодирование состояний УА Мура в виде сети Петри, что позволит исключить традиционный синтез автомата по таблице переходов. А это позволит добиться минимизации логической схемы автомата с целью повышения его быстродействия. А также, такой синтез позволит реализацию параллельного управления.

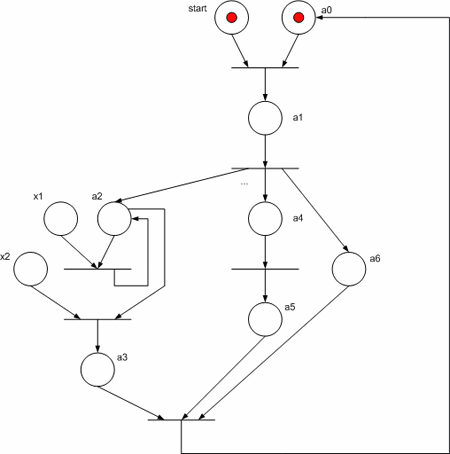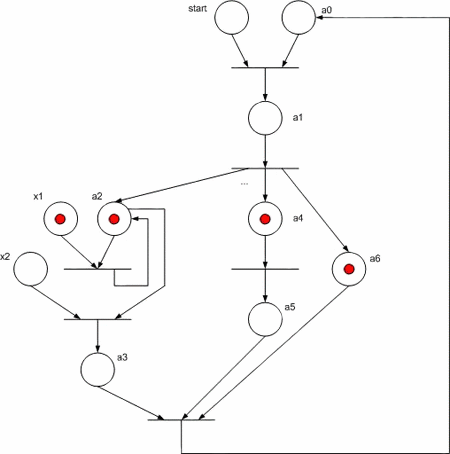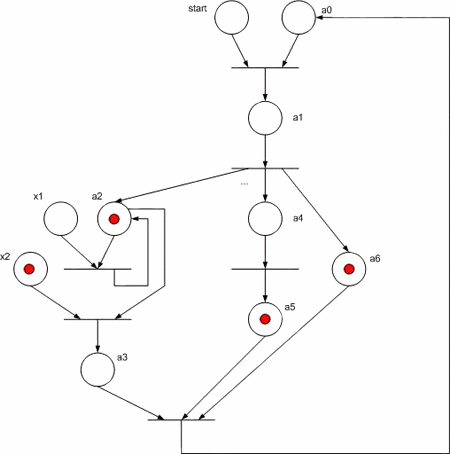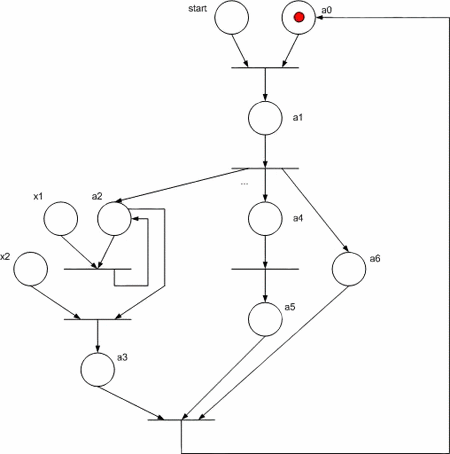
Рассмотрим реализацию УА Мура в виде сети Петри, заданного на рис. 3. Обратим внимание на то, что ветви алгоритма а3 –> a4 и a6 –> a7 выполняются параллельно.

Для реализации схемы данного автомата на FPGA необходимо заменить компоненты сети Петри на рис. 4 их функциональными аналогами: позиция состояния автомата – D–триггером, перехода – элементом "И", множество входов в позицию объединяется элементами "ИЛИ", дугам, соединяющим места и переходы соответствуют обычные электрические соединения. На рис. 5 показана функциональная схема УА, полученная для ГСА из сети Петри.

Рисунок 3 - Исходная граф-схема алгоритма

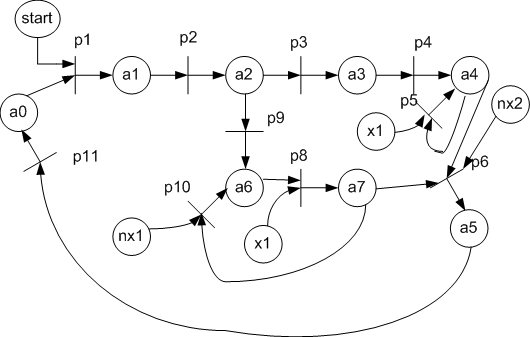
Рисунок 4 - Сеть Петри для исходной ГСА

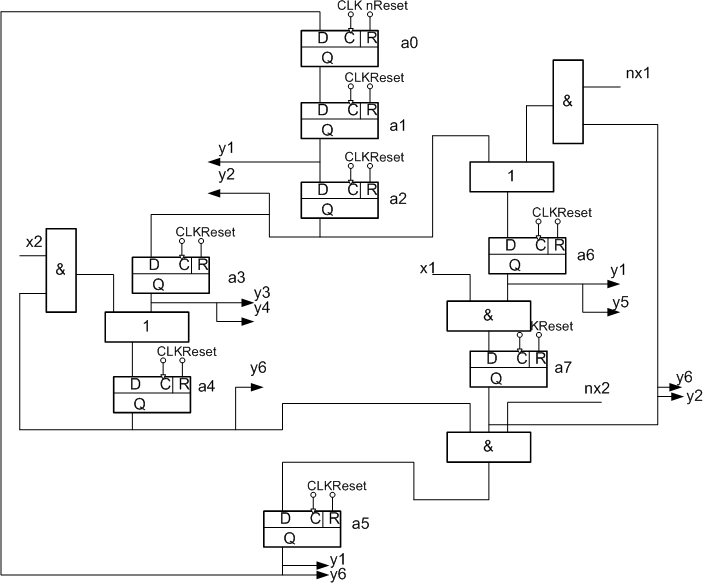
Рисунок 5 - Функциональная схема УА Мура по ГСА

Схема работает следующим образом. По сигналу Reset="1" все триггера, кроме нулевого, сбрасываются в "0", а триггер a0 при этом сигнал устанавливается в 1, что соответствует исходному состоянию, поскольку при этом не вырабатывается никаких управляющих сигналов (это и есть сигнал start). В каждом такте CLK в один или несколько (если в параллельных ветвях) триггеров записывается "1", что соответствует переходу из одного состояние в другое. При этом в триггер, из которого происходит запись "1", записывается "0". Для обеспечения корректной работы схемы сигнал reset должен иметь длительность не более одного такта и вырабатываться один раз при запуске УА.

Третий раздел. Предложена методика автоматизации процесса синтеза УА Мура. Разработано ПО, реализующее автоматизированное проектирование схемы автомата на языке VHDL.

Четвертый раздел. Предложен метод оценки эффективности параллельного УА Мура на FPGA. Определена область эффективного применения УА Мура по предложенной структуре.

Важное замечание. При написании данного автореферата магистерская работа ещё не завершена. Окончательное завершение: декабрь 2009-го года. Полный текст работы и материалы по теме могут быть получены у автора или её руководителя после указанной даты.

Литература

1. Грушвицкий Р.И. Проектирование систем на микросхемах программируемой логики / Р.И. Грушвицкий, А.Х. Мурсаев, Е.П. Угрюмов – СПб., БХВ-Петербург, 2002. – 608с.
2. Баркалов А.А. Синтез автомата Мура на FPGA с унитарным кодированием состояний / А.А. Баркалов, А.А. Красичков, Халед Баракат.
3. Захаров Н. Г. Синтез цифровых автоматов: Учебное пособие / Н.Г. Захаров, В.Н. Рогов – Ульяновск: УлГТУ, 2003 – 544с.
4. Котов В. Е. Сети Петри. – М.: Наука, 1984 – 263с.
5. Лазарев В.Г. Синтез управляющих автоматов / В.Г. Лазарев, Е.И. Пийль – М., Энергоатомиздат, 1989 – 328с.
6. Питерсон Дж. Теория сетей Петри и моделирование систем. – М.: Мир, 1984 – 368с.
7. Учебное пособие "Синтез цифровых автоматов" - http://venec.ulstu.ru/lib/2003/5_Zaharov_Rogov.pdf
8. Структурные модели конечных автоматов при их реализации на ПЛИС - http://www.chipinfo.ru/literature/chipnews/200209/1.html
9. Теория сетей Петри - http://ru.wikipedia.org/wiki/Сети_Петри
10. Немченко А.В. - Параллельные цифровые автоматы - http://www.softcraft.ru/auto/etc/avn/avn1.shtml

• Автобиография
• Автореферат
• Библиотека
• Ссылки
• Отчёт о поиске
• Индивидуальное задание