Автореферат

ЗАГАЛЬНА ХАРАКТЕРИСТИКА РОБОТИ

Актуальність. У наш час відбувається автоматизація процесів у всіх сферах знань навколишнього світу. У деяких сферах застосування ця автоматизація зводиться до створення програмного забезпечення для персонального комп'ютера, але в більшості випадків вимагає створення спеціалізованих ЕОМ. Для організації роботи ЕОМ, як одна з її складових, необхідний керуючий автомат. У його функції входить формування керуючих сигналів, на основі деякого алгоритму для операційної частини ЕОМ.

Алгоритм управління системи задається кодом управління, що надходить в КА із зовнішнього середовища. Алгоритм управління ОА називається мікропрограмою і реалізується керуючим автоматом. Однією з основних проблем при створенні спеціалізованої ЕОМ є пошук компромісу між швидкодією, вартістю і універсальністю КА. Також важливим є час проектування і реалізації схеми КА.

Як відомо, КА з жорсткою логікою виграють за швидкодією перед автоматами з програмованою логікою, але мають жорстку структуру і не можуть бути змінені. ПЛІС дозволяють замінити весь пристрій конфігурований на мікросхему. Таким чином з'являється можливість створювати перепрограмовані КА з жорсткою логікою [1] .

Кінцевий автомат представляє собою найбільш загальну математичну модель цифрового пристрою або цифрової системи. Тому дуже важливо при розробці різних цифрових пристроїв і систем застосовувати ефективні методи синтезу кінцевих автоматів. В той самий час, реалізовані у відомих пакетах автоматизованого проектування (фірм Altera, Xilinx та інших) методи синтезу основані на традиційних підходах, які не дозволяють ефективно використовувати архітектурні можливості нової елементної бази.

Традиційно синтез керуючого автомату виконується за заданою базовою структурою, а оптимізація схеми досягається за рахунок ряду методів, таких як оптимальне кодування станів, виділення підрівнів у комбінаційних схемах і трансформація кодів об’єктів. У той самий час у операційному автоматі гілки алгоритму можуть реалізовуватися паралельно для досягнення максимальної швидкодії ОА. При традиційної реалізації керуючого автомату Мура керування таким ОА повинно здійснюється декількома керуючими автоматами за ієрархічним принципом. Що у свою чергу зменшує швидкодію керуючого автомату за рахунок збільшення обсягу послідовної КЛС.

Найбільший внесок у наукові досягнення, що стосуються автоматизації проектування і тестування цифрових систем, зробили такі вчені як В.М. Глушков, С.І. Баранов, О.О. Баркалов, В.А. Скляров, О.В. Палагін, Г.І. Новіков.

Зв’язок роботи з науковими програмами, планами, темами.

Магістерська робота виконується у 2008 році відповідно науковому напрямку кафедри “Електронні обчислювальні машини” Донецького національного технічного університету.

Мета дослідження – збільшення продуктивність операційного пристрою за рахунок організації паралельної роботи керуючого автомату.

Мета досягається шляхом рішення таких задач дослідження:

1. Розпаралелювання алгоритму керування.
2. Зменшення обсягу послідовної КЛС.
3. Розробка структури та принципів роботи паралельного керуючого автомату з жорсткою логікою на базі FPGA.

Об’єкт дослідження – паралельний керуючий автомат на базі мережі Петрі.

Предмет дослідження – схема переходів паралельного керуючого автомату.

Методи дослідження представлені апаратами булевої алгебри, теорії множин і графів, теорії мереж Петрі і мовами опису апаратури.

Наукова новизна отриманих результатів визначається наступними положеннями :

• запропонована нова структура КА Мура на базі мережі Петрі з декількома паралельними станами;
• розроблений метод синтезу запропонованої структури.

Практична значимість отриманих результатів:

• реалізація КА Мура на базі мережі Петрі найбільш оптимально реалізується на ПЛІС з архітектурою FPGA, що призводить до вигідної оптимізації ресурсів ПЛІС;
• запропонований метод синтезу КА Мура дозволяє легко автоматизувати процес синтезу;
• розпаралелювання алгоритмів обчислення збільшує продуктивність системи в цілому.

ОСНОВНИЙ ЗМІСТ РОБОТИ

Вступ містить обґрунтування актуальності наукової задачі, що розв’язується, формулювання мети, об’єкту і задач дослідження, сукупність наукових результатів, що виносяться на захист, відомості про їх апробації.

Перший розділ. Поява у 1978 році простішої програмованої логічної інтегральної схеми (ПЛІС) фірми Monolithic Memories, що дозволяється реконфігорувати пристрій, що розробляється без повторного проектування друкованої плати, серйозно вплинуло на структуру ринку напівпровідникових приладів. Зараз виробники пропонують багато різноманітних ПЛІС: програмовані прості, матричні і складні логічні пристрої (SPLD, PAL, CPLD), а також базові матричні мікросхеми, що програмуються користувачем (FPGA) зі специфічними характеристиками и сполученням таких параметрів, як швидкодія, енергоспоживання, рівень інтеграції і вартість.

У наш час у якості функціонального базису для реалізації цифрових схем використовується, в основному, FPGA. Сьогодні мікросхеми з FPGA-архітектурою намагаються "перехватити ініціативу" на ринку у структурованих ASIC, надає розробникам необхідні пристрої з високими щільністю розташування елементів і швидкодією, низькими енергоспоживанням і питомою вартістю у розрахунку на вентиль.

Основний ресурс мікросхем з архітектурою FPGA, що програмується, – так звана логічна комірка. До її складу належать генератор логічних функцій, або логічний блок, що програмується (КЛБ, CLB), робота якого задається таблицею істинності (Look-Up Table – LUT), тригер і деяка кількість спеціалізованих ресурсів, що полегшує реалізацію типових для цифрової схемотехніки вузлів. Логічні комірки створюють прямокутну матрицю, яка оточена блоками вводу-виводу IOB, що забезпечують підключення внутрішніх ліній до зовнішніх виводів корпусу ПЛІС.

Традиційно синтез КА виконується за базовою структурою, наприклад, для КА Мура класична структура приведена на рис. 1.

Рисунок 1 - Базова структура КА Мура

При унітарному кодуванні станів КА Мура дешифратор не потрібний, що у свою чергу призводить до спрощення системи функцій збудження регістру Рг.

До складу кожного КЛБ належить D-тригер, що дозволяє найбільш оптимально реалізувати на FPGA схеми з деревовидною структурою і великою кількістю станів, зокрема, мережі Петрі. Автомат Мура з унітарним кодуванням станів можна представити у вигляді мережі Петрі, що дозволить виключити традиційний синтез автомату за ПСТ.

Модель мережі Петрі є принципово асинхронною і служить для відображення і аналізу причинно-слідчі зв’язків у системі. Для прив’язки до визначених моментів часу тих чи інших переходів використовуються події.

Простою мережею Петрі зветься набор N=(S,T,M,P,F), де:

1. S = {s₁, …, s_N} – множина місць;
2. T = {t₁, …, t_N} – множина переходів таких, що S ∩ T = 0;
3. M = {m₁, …, m_N} – множина міток;
4. P = {p₁, …, p_N} – множина подій;
5. F ⊆ μS×T×μS – відношення інцидентності таке, що
   а) ∀(S'₁, t₁, S"₁), (S'₂, t₂, S"₂) ∈ F : (S'₁, t₁, S"₁) ≠ (S'₂, t₂, S"₂) ⇒ t₁ ≠ t₂;
   б) {t| <S', t, S"> ∈ F} = T.

Умови у пункті 5 говорять, що для кожного переходу t ∈ T існує єдиний елемент <S', t, S"> ∈ F, що задає для нього вхідну множину місць S' і вихідну множину S".

Мережа Петрі має наглядну форму представлення у вигляді графу, до якого належать чотири базових елементи: позиції (місця), переходи, дуги та мітки. На рис. 2 наведено приклад такого графу.

Функціонування мережі полягає у переміщенні міток m₁-m₃ дугами між місцями S₁-S₃ і формуванні подій. Переходи t₁-t₂ задають умови переміщень меток з місць S₁ і S₃. Вихідне розташування меток по місцях є початковою умовою і може бути вільним [2].

Виходячи з цього, довільна граф-схема алгоритму (ГСА) для КА, є окремим випадком мережі Петрі з однією міткою, яка відповідає поточному стану автомату. Множина місць S відповідає множині станів автомату, множина переходів t – множині умовних вершин, множина подій – множині наборів керуючих сигналів.

Таким чином, довільний КА може бути представленим у вигляді мережі Петрі. У тому випадку, якщо події виникають за наявністю метки у визначеному місці, мережа відображає поведінку КА Мура. Якщо подія формується у час переміщення меток між місцями, залежно від переходів, то мережа відображає поведінку автомату Мілі.

Дана схема реалізується на FPGA одним з відомих методів.

Перевагою такої реалізації КА на FPGA є:

1. Ідентичність блоків і регулярність структури автомату.
2. Мінімальна комбінаційна частина, розподілена по всій схемі FPGA.
3. Невелика кількість входів комбінаційних схем, що не залежить від кількості станів автомату.
4. Висока швидкодія автомату.
5. Відсутність традиційного синтезу.

До недоліків методу слід віднести те, що число станів автомату не може перевищувати число тригерів заданої мікросхеми FPGA, що часто відповідає числу КЛБ.

Другий розділ.

Передбачається застосувати унітарне кодування станів КА Мура у вигляді мережі Петрі, що дозволяє виключити традиційний синтез автомату за таблицею переходів. А це дозволить досягти мінімізації логічної схеми автомату з метою підвищення його швидкодії. А також, такий синтез дозволить реалізацію паралельного керування.

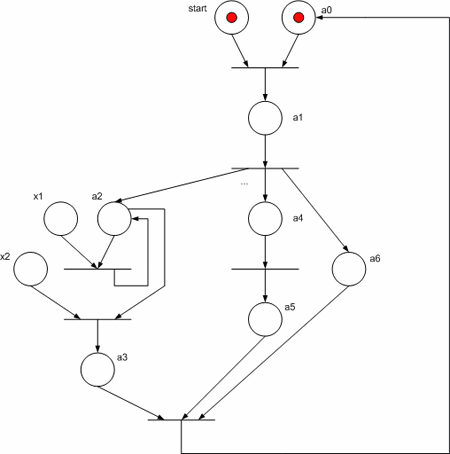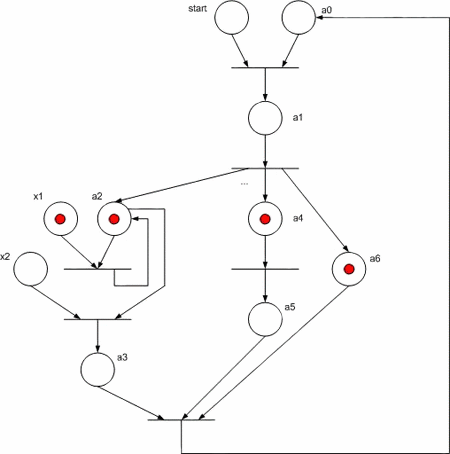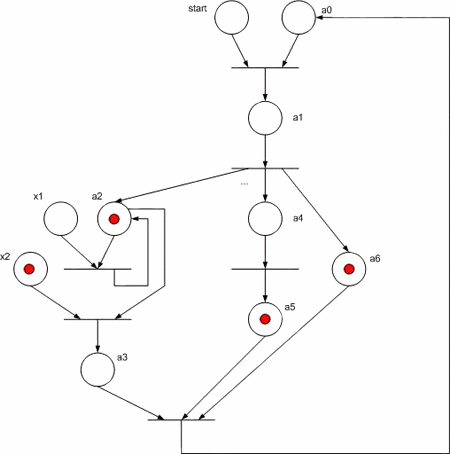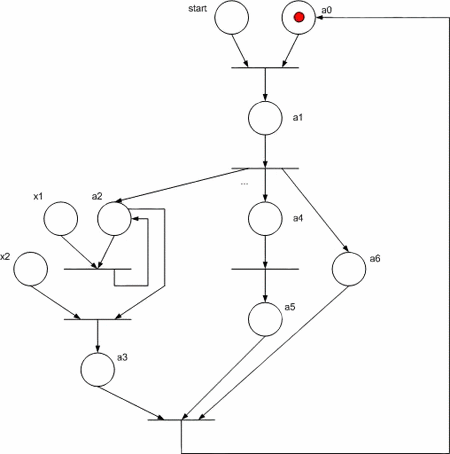
Розглянемо реалізацію КА Мура у вигляді мережі Петрі, заданого на рисунку 3. Звернемо увагу на те, що гілки алгоритму а3 –> a4 і a6 –> a7 виконуються паралельно.

Для реалізації схеми даного автомату на FPGA необхідно замінити компоненти мережі Петрі на рисунку 4 їх функціональними аналогами: позиція стану автомату – D – тригером, переходу – елементом «І», множина входів до позиції об’єднується елементами «АБО», дугам, що з’єднують місця і переходи відповідають звичайні електричні зв’язки. На рисунку 5 показана функціональна схема КА, що отримана для ГСА з мережі Петрі.

Рисунок 3 - Вихідна граф-схема алгоритму

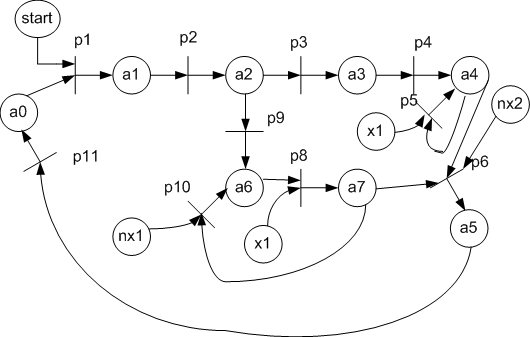
Рисунок 4 - Мережа Петрі для вихідної ГСА

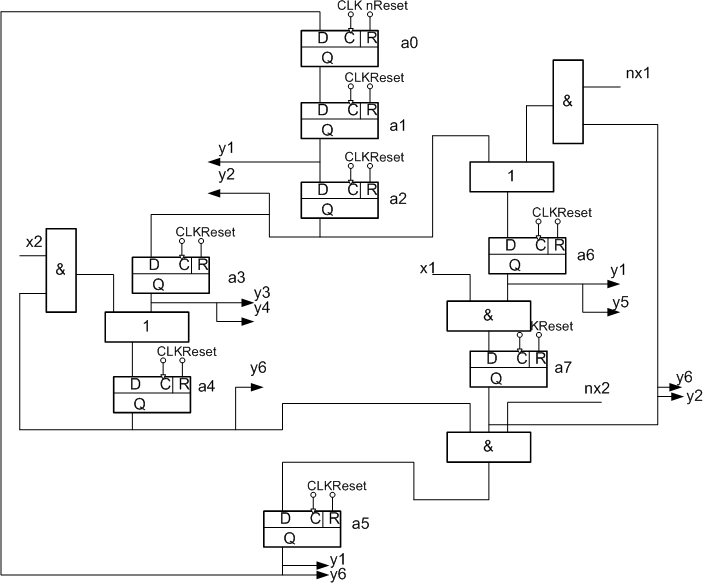
Рисунок 5 - Функціональна схема КА Мура за ГСА

Схема працює наступним чином. За сигналом Reset=”1” усі тригери, крім нульового, скидаються у “0”, а тригер a0 при цьому сигнал встановлюється у 1, що відповідає вихідному стану, оскільки при цьому не виробляються ніяких керуючих сигналів (це і є сигнал start). У кожному такті CLK до одного чи декількох (якщо у паралельних гілках) тригерів записується “1”, що відповідає переходу з одного стану до іншого. При цьому до тригеру, з якого здійснюється запис “1”, записується “0”. Для забезпечення коректної роботи схеми сигнал reset повинен мати тривалість не більш одного такту і видаватися один раз при запуску КА.

Третій розділ. Запропонована методика автоматизації процесу синтезу КА Мура. Розроблено ПЗ, що реалізує автоматизації проектування схеми автомату на мові VHDL.

Четвертий розділ. Запропонований метод оцінки ефективності паралельного КА Мура на FPGA. Визначена область ефективного застосування КА Мура за запропонованою структурою.

Важливе зауваження. При написаннні даного автореферату магістрську роботу ще не завершено. Кінцеве завершення: грудень 2009-го року. Повний текст роботи і матеріали по темі можуть бути отримані у автора або її керівника після вказаної дати.

Література

1. Грушвицкий Р.И. Проектирование систем на микросхемах программируемой логики / Р.И. Грушвицкий, А.Х. Мурсаев, Е.П. Угрюмов – СПб., БХВ-Петербург, 2002. – 608с.
2. Баркалов А.А. Синтез автомата Мура на FPGA с унитарным кодированием состояний / А.А. Баркалов, А.А. Красичков, Халед Баракат.
3. Захаров Н. Г. Синтез цифровых автоматов: Учебное пособие / Н.Г. Захаров, В.Н. Рогов – Ульяновск: УлГТУ, 2003 – 544с.
4. Котов В. Е. Сети Петри. – М.: Наука, 1984 – 263с.
5. Лазарев В.Г. Синтез управляющих автоматов / В.Г. Лазарев, Е.И. Пийль – М., Энергоатомиздат, 1989 – 328с.
6. Питерсон Дж. Теория сетей Петри и моделирование систем. – М.: Мир, 1984 – 368с.
7. Учебное пособие "Синтез цифровых автоматов" - http://venec.ulstu.ru/lib/2003/5_Zaharov_Rogov.pdf
8. Структурные модели конечных автоматов при их реализации на ПЛИС - http://www.chipinfo.ru/literature/chipnews/200209/1.html
9. Теория сетей Петри - http://ru.wikipedia.org/wiki/Сети_Петри
10. Немченко А.В. - Параллельные цифровые автоматы - http://www.softcraft.ru/auto/etc/avn/avn1.shtml

• Автобіографія
• Автореферат
• Бібліотека
• Посилання
• Звіт про пошук
• Індивідуальне завдання (російською)