
Soldatov Kyrylo
Faculty: Computer Science
Speciality: System Programming
Theme of master's work:
Synthesis of Moore finite state machine with an extention of state codes
Scientific advisers: Barkalov A.A., Malcheva R.V.
Introduction
Model of Moore finite state machine (FSM) [1] is often used during the
digital control systems realization [2, 3]. The microelectronic development has led to ap-pearance of different programmable
logic devices [4, 5], one of which are CPLD (complex programmable logic devices) [6, 7, 9, 10]. The base of CPLD is macrocell PAL
(programmable array logic), are connected by the programmable arrays of in-terconnections. One of the important problems of
FSM synthesis on CPLD is a minimization of macrocells’ number of its logical circuit. One of the ways to solve this problem
is optimal states’ coding [8]. However this approach does not allow optimization of the output signals generation circuit.
In this work an optimization method is proposed. It is based on representation of the next state code as a con-catenation
of codes for class of pseudoequivalent states and collection of microop-erations. Such an approach allows reducing of
hardware amount in FSM circuits and does not lead to speed loss.
The aim of research is an optimization of Moore FSM by the non-standard
representation of the states’ codes.
The task of research is developing of the method for Moore FSM synthesis to reduce
the number of PAL cells in automata scheme. A control algorithm is represented as a graph-scheme of algorithm (GSA)
[1].
The general aspects and the basic idea of a proposed method
Let Moore FSM be represented by the direct structure table (DST) with
col-umns [1]: am, K(am), as, K(as), Xh, Фh, h.
Here am is an initial state of FSM; K(am) is a code of state 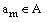 of capacity
of capacity  , to code the states the internal variables from set
, to code the states the internal variables from set  ;
as, K(as) are a state of transition and its code spectively; Xh is an input, which
determines the transition m,as>, and equal to conjunction of some elements (or their negations)
of a logic conditions set
;
as, K(as) are a state of transition and its code spectively; Xh is an input, which
determines the transition m,as>, and equal to conjunction of some elements (or their negations)
of a logic conditions set 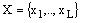 ; Фh is a set of input memory functions for flip-flops of FSM
memory, is set for memory switching from К(am) to К(as),
; Фh is a set of input memory functions for flip-flops of FSM
memory, is set for memory switching from К(am) to К(as),  ; h=1,…,Н is a
number of transition. In column am, a set of microoperations Yqis written, which is generated in state
; h=1,…,Н is a
number of transition. In column am, a set of microoperations Yqis written, which is generated in state
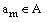 , where
, where  This table is a basis to form the system of functions
This table is a basis to form the system of functions

(1)

(2)
are determined FSM logic circuit. Systems (1)-(2) are describe the structural circuit of Moore U1- FSM, is shown
on fig.1. In this structure memory excitation function circuit (MFC) realizes the system (1), flip-flop RG saves states’
codes, microoperation circuit (MOC) realizes the system (2). To minimize the amount of marcocells PAL in MFC an optimal
states’ coding method can be used [8]. It allows to decrease the amount of terms in system (1) up to Н0.
Fig.1. The structural diagram of FSM Moore U1
Here Н0 – number of transitions of equivalent Mealy FSM. MOC optimization can be done by the use of accurate state
coding [10]. Meanwhile the number of macrocells can be decreased up to N, that corresponds to situation, when every function
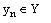 is realized on single macrocell. For optimal and accurate states’ coding, for example, known
algorithm ESPRESSO [3] can be used. But both methods can’t be implicated at the same time. That is why states’ coding allows
to optimize MFC or MOC.
is realized on single macrocell. For optimal and accurate states’ coding, for example, known
algorithm ESPRESSO [3] can be used. But both methods can’t be implicated at the same time. That is why states’ coding allows
to optimize MFC or MOC.
In this paper a method for reduction of hardware amount in both logic
circuit of Moore finite state machine is proposed.
One of Moore FSM features is exist of pseudoequivalent states [8] –
states with the same transitions by the effect of the same inputs. Such states correspond to the control algorithm operator
nodes [1], outputs of which are connected with an input of the same node.
Let  partition of a set А on groups of
pseudoequivalent states. To code groups
partition of a set А on groups of
pseudoequivalent states. To code groups 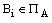 with binary codes K(Bi) of capacity
with binary codes K(Bi) of capacity
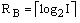
. (3)
Let initial GCA G includes Q to by to different sets of microoperations (SМО) 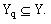 To code set Yq with binary code K(Yq) of capacity
To code set Yq with binary code K(Yq) of capacity
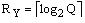
. (4)
Let operator node bt of GCA G is correspond to a state  and let a set of microoperations Yq. Then code of state
and let a set of microoperations Yq. Then code of state 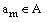 can be represented as a
concatenation of codes
can be represented as a
concatenation of codes

. (5)
Such representation allows to present Moore FSM in model U2 (fig.2).
Fig.2. The structural diagram of FSM Moore U2
In automata U2 circuit MFC realizes function (6) and circuit MOC – function (7).

(6)

(7)
Thus set units  are used for coding of classes
are used for coding of classes
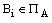 , and set units
, and set units 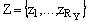 are used for coding of sets of microoperations.
are used for coding of sets of microoperations.
The offered approach has a number of merits:
- Codes of classes do not depend on codes of microoperations (and on the contrary). Therefore classes can be encoded so
that to simplify circuit MOC.
- The number of lines of jump table FSM U2 always equals Н0and does not depend on a method of coding
of states.
It is enough for coding of states FSM U1
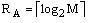
(8)
Conclusion
The offered method of representation of codes of states of transition is
oriented to reduction of number of macrocells PAL in the circuit of the automatic machine of Moore. Such approach allows
to reduce number of terms in system of functions of excitation of memory to the value of appropriate parameter of the
equivalent automatic machine of Mile. Researches have shown that the offered method always is more effective in comparison
with a classical method of implementation FSM of Moore. Thus the number of macrocells decreases to 38%.
Reduction of number of macrocells is not linked to introduction of the
additional blocks reducing speed of the circuit. Moreover, reduction of number of macrocells is often accompanied by
reduction of number of levels of circuit FSM. Speed FSM and, therefore, digital system as a whole thus raises.
Scientific novelty of the offered method consists in usage of features
of the automatic machine of Moore (presence of classes of pseudo-equivalent states) for optimisation of number of macrocells
PAL in the automatic machine logic circuit.
The practical significance of a method consists in reduction of square
of the chip occupied with combinative circuit FSM that allows to receive circuits which possess smaller cost, than known
clones from the literature.
Further directions of operation are linked to research of possibility of
application of the offered method for a case of implementation of the control unit in basis FPGA, and also as a part of
"systems-on-kristale".
Literature
- Baranov S. Logic Synthesis for Control Automata. – Kluwer Academic Publishers, 1994. – 312 pp.
- Соловьев В.В. Проектирование цифровых схем на основе программируемых логических интегральных схем. – М.:
Горячая линия - ТЕЛЕКОМ, 2001. – 636 с.
- DeMicheli G/ Synthesis and Optimization of Digital Circuits. – McGraw-Hill, 1994. – 636 pp.
- Грушницкий Р.И. Проектирование систем с использованием микросхем программируемой логики / Р.И. Грушницкий,
А.Х. Мурзаев, Е.П. Угрюмов. – СПб.: БХВ. - Петербург, 2002. –608 с.
- Maxfield C. The Design Warrior’s Guide to FPGAs. – Amsterdam: Elseveir, 2004. – 541 pp.
- Баркалов А.А. Принципы оптимизации логической схемы микропрограммного автомата Мура // Кибернетика и
системный анализ. – 1998. – № 1. – С. 65-72.
- Nababi Z. Emvedded Core Design with FPGA. – NY: McGraw-Hill, 2008, - 618pp.
- Yang S. Logic Synthesis and Optimization Benchmarks user guide. Technical report, №1991 – IWLS-UG-Saryang.-Microelectronics center of North Carolina.
- The site of the leading manufacturer of FPGA [Electronic resource] Altera
- The site of the leading manufacturer of CPLD [Electronic resource] Xilinx
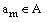 of capacity
of capacity  , to code the states the internal variables from set
, to code the states the internal variables from set  ;
as, K(as) are a state of transition and its code spectively; Xh is an input, which
determines the transition
;
as, K(as) are a state of transition and its code spectively; Xh is an input, which
determines the transition 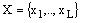 ; Фh is a set of input memory functions for flip-flops of FSM
memory, is set for memory switching from К(am) to К(as),
; Фh is a set of input memory functions for flip-flops of FSM
memory, is set for memory switching from К(am) to К(as),  ; h=1,…,Н is a
number of transition. In column am, a set of microoperations Yqis written, which is generated in state
; h=1,…,Н is a
number of transition. In column am, a set of microoperations Yqis written, which is generated in state
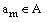 , where
, where  This table is a basis to form the system of functions
This table is a basis to form the system of functions (1)
(1) (2)
(2)
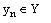 is realized on single macrocell. For optimal and accurate states’ coding, for example, known
algorithm ESPRESSO [3] can be used. But both methods can’t be implicated at the same time. That is why states’ coding allows
to optimize MFC or MOC.
is realized on single macrocell. For optimal and accurate states’ coding, for example, known
algorithm ESPRESSO [3] can be used. But both methods can’t be implicated at the same time. That is why states’ coding allows
to optimize MFC or MOC.
 partition of a set А on groups of
pseudoequivalent states. To code groups
partition of a set А on groups of
pseudoequivalent states. To code groups 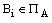 with binary codes K(Bi) of capacity
with binary codes K(Bi) of capacity
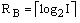 . (3)
. (3)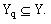 To code set Yq with binary code K(Yq) of capacity
To code set Yq with binary code K(Yq) of capacity
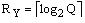 . (4)
. (4) and let a set of microoperations Yq. Then code of state
and let a set of microoperations Yq. Then code of state  . (5)
. (5)
 (6)
(6) (7)
(7) are used for coding of classes
are used for coding of classes
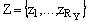 are used for coding of sets of microoperations.
are used for coding of sets of microoperations.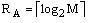 (8)
(8)