
Солдатов Кирилл Альбертович
Факультет вычислительной техники и информатики
Специальность: Системное программирование
Тема магистерской работы:
Синтез автомата Мура с расширением кодов состояний перехода
Научный руководитель: Баркалов А.А., Мальчева Р.В.
Введение
Хотелось бы начать автореферат с обзора исследований разработок по данной теме на трех уровнях:
- глобальном (мировом);
Цифровые автоматы - это то, что сейчас окружает современного человека. Они повсюду: начиная от домофона и заканчивая микроволновой печью. Поэтому мне кажется излишне говорит, что цифровые автоматы на мировом уровен занимают одну из ведущих позиций. Чтобы убедиться, что цифровые автоматы - это сегодняшний и завтрашний день достаточно зайти на ссылку FSMGen и убедиться в этом самому. Раз всемирное сообщество программистов решило создать программу для построения XML-файла конечного автомата, то это уже о много говорит;
- национальном (занимается ли кто-то данной темой в Украине за пределами ДонНТУ);
В нашей стране, к сожалению, не так уж много хороших технических ВУЗов, в которых была бы хороша освещена данная проблема. В г. Донецке в Институте Искусственного Интеллекта имеется Кафедра технической информатики, в Национальном Авиационном Университете - Институт электроники и систем управления, а также в г. Харькове, в Харьковском национальном университете радиоэлектроники - Кафедру автоматизации проектирования вычислительной техники;
- локальном (занимаются ли текущие магистранты или выпустившиеся магистры данной темой);
В нашем университете достаточно хорошо уделено внимание цифровым автоматам. Под руководством Баркалова А.А., Ковалева С.А, Мальчевой Р.В. были выпущены следующий магистры, которые занимались данной тематикой:
Лаврик Александр Сергеевич занимался исследованием композиционных устройств управления с модифицированной системой микрокоманд на ПЛИС;
Мирошкин Александр Николаевич занимался исследованием композиционных устройств управления с базовой структурой;
Цололо Сергей Алексеевич занимался исследованием методов синтеза устройств управления на программируемых пользователем вентильных матрицах.
Модель микропрограммного автомата (МПА) Мура [1]
часто используется при реализации устройств управления цифровых систем [2, 3]. Развитие микроэлектроники
привело к появлению разнообразных программируемых логических устройств [4, 5], одними из представителей
которых являются CPLD (complex programmable logic devices) [6, 7, 9, 10]. Основой CPLD являются макроячейки
PAL (pro-grammable array logic), соединенные с помощью программируемых матриц межсоединений. Одной из
важных проблем, возникающих при синтезе МПА на CPLD, является минимизация числа макроячеек в его логической схеме.
Одним из путей решения этой проблемы является оптимальное кодирование состояний [8]. Однако этот подход не позволяет
оптимизировать схему формирования выходных сигналов. В настоящей работе предлагается метод оптимизации, основанный на
представлении кода состояния МПА в виде конкатенации кодов класса псевдоэквивалентных состояний и кода набора микроопераций
(микрокоманды). Такой подход позволяет уменьшить аппаратурные затраты в комбинационных блоках МПА и не приводит к потере
быстродействия.
Целью исследования является оптимизация схемы МПА Мура за счет нестандартного
представления кодов состояний.
Задачей исследования является разработка метода синтеза МПА Мура, позволяющего
уменьшить число ячеек PAL в схеме автомата. При этом алгоритм управления представляется в виде граф-схемы алгоритма (ГСА) [1].
Общие положения и основная идея предлагаемого метода
Пусть автомат Мура задан прямой структурной таблицей (ПСТ)
со столбцами [1]: am, K(am), as, K(as), Xh, Фh, h.
Здесь am - исходное состояние МПА; K(am) – код состояния 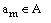 разрядности
разрядности  , для кодирования состояний используются внутренние переменные из множества
, для кодирования состояний используются внутренние переменные из множества
 ; as, K(as) – соответственно состояние перехода и его код;
Xh – входной сигнал, определяющий переход m,as>, и равный конъюнкции некоторых
элементов (или их отрицаний) множества логических условий
; as, K(as) – соответственно состояние перехода и его код;
Xh – входной сигнал, определяющий переход m,as>, и равный конъюнкции некоторых
элементов (или их отрицаний) множества логических условий 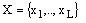 ; Фh – набор функций
возбуждения триггеров памяти МПА, принимающих единичное значение для переключения памяти из К(am) в
К(as),
; Фh – набор функций
возбуждения триггеров памяти МПА, принимающих единичное значение для переключения памяти из К(am) в
К(as),  ; h=1,…,Н – номер перехода. В столбце am записывается набор
микроопераций Yq, формируемых в состоянии
; h=1,…,Н – номер перехода. В столбце am записывается набор
микроопераций Yq, формируемых в состоянии 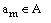 , где
, где  Эта таблица
является основой для формирования систем функций
Эта таблица
является основой для формирования систем функций

(1)

(2)
задающих логическую схему МПА. Системы (1)-(2) определяют структурную схему МПА Мура U1, показанную на рис.1.
В этой структуре блок функций возбуждения памяти (БФП) реализует систему (1), регистр RG служит для хранения кодов состояний,
а блок микроопераций (БМО) реализует систему (2). Для минимизации числа макроячеек PAL в БФП может использоваться метод
оптимального кодирования состояний [8], позволяющий уменьшить число термов в системе (1) до Н0.
Рис.1 Структурная схема автомата Мура U1 (11 кадров, задержка между кадрами - 0.5 сек, количество повторений - 5)
Здесь Н0 – число переходов эквивалентного автомата Мили. Оптимизация БМО может быть выполнена за счет
уточненного кодирования состояний [10]. При этом число макроячеек может быть уменьшено до N, что соответствует ситуации,
когда каждая функция 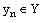 реализуется на одной макроячейке. Для оптимального и уточненного кодирования
состояний может быть использован, например, известный алгоритм ESPRESSO [3]. Однако оба метода не могут быть применены
одновременно. Поэтому кодирование состояний позволяет оптимизировать либо БФП, либо БМО.
реализуется на одной макроячейке. Для оптимального и уточненного кодирования
состояний может быть использован, например, известный алгоритм ESPRESSO [3]. Однако оба метода не могут быть применены
одновременно. Поэтому кодирование состояний позволяет оптимизировать либо БФП, либо БМО.
В настоящей работе предлагается метод, позволяющий оптимизировать
число PAL в схемах обоих блоков МПА Мура.
Одной из особенностей МПА Мура является наличие псевдоэквивалентных
состояний [8], то есть состояний с одинаковыми переходами под воз-действием одинаковых входных сигналов. Такие состояния
соответствуют операторным вершинам [1] алгоритма управления, выходы которых связаны со входом одной и той же вершины
алгоритма.
Пусть  - разбиение множества А на классы
псевоэквивалентных состояний. Закодируем классы
- разбиение множества А на классы
псевоэквивалентных состояний. Закодируем классы 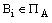 двоичными кодами K(Bi) разрядности
двоичными кодами K(Bi) разрядности
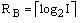
. (3)
Пусть исходная ГСА Г включает Q попарно различных наборов микроопераций (НМО) 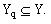 Закодируем набор Yq двоичным кодом K(Yq) разрядности
Закодируем набор Yq двоичным кодом K(Yq) разрядности
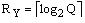
. (4)
Пусть операторная вершина bt ГСА Г соответствует состоянию  и пусть в ней записан набор микроопераций Yq. Тогда код состояния
и пусть в ней записан набор микроопераций Yq. Тогда код состояния 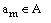 можно представить
в виде конкатенации кодов
можно представить
в виде конкатенации кодов

. (5)
Такое представление позволяет представить автомат Мура в виде модели U2 (рис.2).
Рис.2 Структурная схема автомата Мура U2
В автомате U2 блок БФП реализует функции (6) и блок БМО – функции (7).

(6)

(7)
При этом элементы множества  используются для
кодирования классов
используются для
кодирования классов 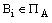 , а элементы множества
, а элементы множества 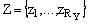 используются для кодирования
наборов микроопераций.
используются для кодирования
наборов микроопераций.
Предлагаемый подход имеет ряд положительных качеств:
- Коды классов не зависят от кодов микроопераций (и наоборот). Поэтому классы можно закодировать так,
чтобы упростить схему БМО.
- Число строк таблицы переходов МПА U2 всегда равняется Н0 и не зависит от
метода кодирования состояний.
Для кодирования состояний МПА U1 достаточно
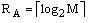
(8)
Заключение
Предлагаемый метод представления кодов состояний перехода ориентирован
на уменьшение числа макроячеек PAL в схеме автомата Мура. Такой подход позволяет уменьшить число термов в системе функций
возбуждения памяти до величины соответствующего параметра эквивалентного автомата Мили. Исследования показали, что
предлагаемый метод всегда более эффективен по сравнению с классическим методом реализации МПА Мура. При этом число
макроячеек уменьшается до 38%.
Уменьшение числа макроячеек не связано с введением дополнительных блоков,
уменьшающих быстродействие схемы. Более того, уменьшение числа макроячеек часто сопровождается уменьшением числа уровней
схемы МПА. При этом повышается быстродействие МПА и, следовательно, цифровой системы в целом.
Научная новизна предложенного метода заключается в использовании
особенностей автомата Мура (наличие классов псевдоэквивалентных состояний) для оптимизации числа макроячеек PAL
в логической схеме автомата.
Практическая значимость метода заключается в уменьшении площади
кристалла, занимаемой комбинационной схемой МПА, что позволяет получить схемы, которые обладают меньшей стоимостью, чем
известные из литературы аналоги.
Дальнейшие направления работы связаны с исследованием возможности применения
предложенного метода для случая реализации устройства управления в базисе FPGA, а также в составе «систем-на-кристале».
Литература
- Baranov S. Logic Synthesis for Control Automata. – Kluwer Academic Publishers, 1994. – 312 pp.
- Соловьев В.В. Проектирование цифровых схем на основе программируемых логических интегральных схем. – М.:
Горячая линия - ТЕЛЕКОМ, 2001. – 636 с.
- DeMicheli G/ Synthesis and Optimization of Digital Circuits. – McGraw-Hill, 1994. – 636 pp.
- Грушницкий Р.И. Проектирование систем с использованием микросхем программируемой логики / Р.И. Грушницкий,
А.Х. Мурзаев, Е.П. Угрюмов. – СПб.: БХВ. - Петербург, 2002. –608 с.
- Maxfield C. The Design Warrior’s Guide to FPGAs. – Amsterdam: Elseveir, 2004. – 541 pp.
- Баркалов А.А. Принципы оптимизации логической схемы микропрограммного автомата Мура // Кибернетика и
системный анализ. – 1998. – № 1. – С. 65-72.
- Nababi Z. Emvedded Core Design with FPGA. – NY: McGraw-Hill, 2008, - 618pp.
- Yang S. Logic Synthesis and Optimization Benchmarks user guide. Technical report, №1991 – IWLS-UG-Saryang.-Microelectronics center of North Carolina.
- Сайт ведущего производителя FPGA [Электронный ресурс] Altera
- Сайт ведущего производителя CPLD [Электронный ресурс] Xilinx
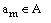 разрядности
разрядности  , для кодирования состояний используются внутренние переменные из множества
, для кодирования состояний используются внутренние переменные из множества
 ; as, K(as) – соответственно состояние перехода и его код;
Xh – входной сигнал, определяющий переход
; as, K(as) – соответственно состояние перехода и его код;
Xh – входной сигнал, определяющий переход 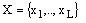 ; Фh – набор функций
возбуждения триггеров памяти МПА, принимающих единичное значение для переключения памяти из К(am) в
К(as),
; Фh – набор функций
возбуждения триггеров памяти МПА, принимающих единичное значение для переключения памяти из К(am) в
К(as),  ; h=1,…,Н – номер перехода. В столбце am записывается набор
микроопераций Yq, формируемых в состоянии
; h=1,…,Н – номер перехода. В столбце am записывается набор
микроопераций Yq, формируемых в состоянии 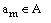 , где
, где  Эта таблица
является основой для формирования систем функций
Эта таблица
является основой для формирования систем функций (1)
(1) (2)
(2)
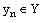 реализуется на одной макроячейке. Для оптимального и уточненного кодирования
состояний может быть использован, например, известный алгоритм ESPRESSO [3]. Однако оба метода не могут быть применены
одновременно. Поэтому кодирование состояний позволяет оптимизировать либо БФП, либо БМО.
реализуется на одной макроячейке. Для оптимального и уточненного кодирования
состояний может быть использован, например, известный алгоритм ESPRESSO [3]. Однако оба метода не могут быть применены
одновременно. Поэтому кодирование состояний позволяет оптимизировать либо БФП, либо БМО.
 - разбиение множества А на классы
псевоэквивалентных состояний. Закодируем классы
- разбиение множества А на классы
псевоэквивалентных состояний. Закодируем классы 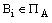 двоичными кодами K(Bi) разрядности
двоичными кодами K(Bi) разрядности
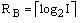 . (3)
. (3)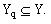 Закодируем набор Yq двоичным кодом K(Yq) разрядности
Закодируем набор Yq двоичным кодом K(Yq) разрядности
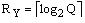 . (4)
. (4) и пусть в ней записан набор микроопераций Yq. Тогда код состояния
и пусть в ней записан набор микроопераций Yq. Тогда код состояния  . (5)
. (5)
 (6)
(6) (7)
(7) используются для
кодирования классов
используются для
кодирования классов 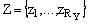 используются для кодирования
наборов микроопераций.
используются для кодирования
наборов микроопераций.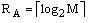 (8)
(8)