
Солдатов Кирило Альбертович
Факультет: Обчислювальної техніки інформатики
Спеціальність: Системне програмування
Тема випускної роботи:
Синтез автомата Мура з розширенням кодів станів переходу
Науковий керівник: Баркалов О.О., Мальчева Р.В.
Вступ
Модель мікропрограмного автомата (МПА) Мура [1] часто використовується
при реалізації пристроїв управління цифрових систем [2, 3]. Розвиток мікроелектроніки привів до появи всіляких програмованих
логічних пристроїв [4, 5], одними з представників яких є CPLD (complex programmable logic devices) [6, 7, 9, 10]. Основою CPLD є
макровічка PAL (pro-grammable array logic), сполучені за допомогою програмованих матриць межсоєдіненій. Одній з важливих
проблем, що виникають при синтезі МПА на CPLD, є мінімізація числа макровічок в його логічній схемі. Однією з доріг
вирішення цієї проблеми є оптимальне кодування станів [8]. Проте цей підхід не дозволяє оптимізувати схему формування
вихідних сигналів. У справжній роботі пропонується метод оптимізації, заснований на представленні коди стану МПА
у вигляді конкатенації код класу псевдоеквівалентних станів і коди набору мікрооперацій(мікрокоманди). Такий підхід дозволяє
зменшити апаратурні витрати в комбіна-ционних блоках МПА і не приводить до втрати швидкодії.
Метою дослідження є оптимізація схеми МПА Мура за рахунок нестандартного
представлення код станів.
Завданням дослідження є розробка методу синтезу МПА Мура, що дозволяє зменшити
число вічок PAL в схемі автомата. При цьому алгоритм управління представляється у вигляді графа-схеми алгоритму (ГСА) [1].
Загальні положення і основна ідея пропонованого методу
Нехай автомат Мура заданий прямою структурною таблицею (ПСТ) із
стовпцями [1]: am, K(am), as, K(as), Xh, Фh, h.
Тут am - вихідний стан МПА; K(am) – код стану 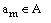 розрядності
розрядності  , для кодування станів використовуються внутрішні змінні з безлічі
, для кодування станів використовуються внутрішні змінні з безлічі
 ; as, K(as) – відповідно стан переходу і його код;
Xh – вхідний сигнал, що визначає перехід m,as>, і рівний кон'юнкції деяких елементів
(або їх заперечень) безлічі логічних умов
; as, K(as) – відповідно стан переходу і його код;
Xh – вхідний сигнал, що визначає перехід m,as>, і рівний кон'юнкції деяких елементів
(або їх заперечень) безлічі логічних умов 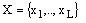 ; Фh – набір функцій збудження тригерів
пам'яті МПА, що набувають одиничного значення для перемикання пам'яті з К(am) до К(as),
; Фh – набір функцій збудження тригерів
пам'яті МПА, що набувають одиничного значення для перемикання пам'яті з К(am) до К(as),
 ; h=1,…,Н – номер переходу. У стовпці am аписується набір мікрооперацій
Yq, що формуються у стані
; h=1,…,Н – номер переходу. У стовпці am аписується набір мікрооперацій
Yq, що формуються у стані 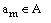 , де
, де  Ця таблиця
є основою для формування систем функцій
Ця таблиця
є основою для формування систем функцій

(1)

(2)
задаючих логічну схему МПА. Системи (1) -(2) визначають структурну схему МПА Мура U1, яка наведена на рис.1.
У цій структурі блок функцій збудження пам'яті (БФП) реалізує систему (1), регістр RG служить для зберігання код станів,
а блок мікрооперацій (БМО) реалізує систему (2). Для мінімізації числа макровічок PAL в БФП може використовуватися метод
оптимального кодування станів [8], що дозволяє зменшити число термів в системі (1) до Н0.
Рис.1 Структурна схема автомата Мура U1
Тут Н0 – число переходів еквівалентного автомата Милі. Оптимізація БМО може бути виконана за рахунок уточненого
кодування станів [10]. При цьому число макровічок може бути зменшене до N, що відповідає ситуації, коли кожна функція
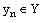 реалізується на одної макрокомірки. Для оптимального і уточненого кодування станів може бути
використаний, наприклад, відомий алгоритм ESPRESSO [3]. Проте обидва методи не можуть бути застосовані одночасно. Тому
кодування станів дозволяє оптимізувати або БФП, або БМО.
реалізується на одної макрокомірки. Для оптимального і уточненого кодування станів може бути
використаний, наприклад, відомий алгоритм ESPRESSO [3]. Проте обидва методи не можуть бути застосовані одночасно. Тому
кодування станів дозволяє оптимізувати або БФП, або БМО.
У справжній роботі пропонується метод, що дозволяє оптимізувати число
PAL в схемах обох блоків МПА Мура.
Однією з особливостей МПА Мура є наявність псевдоеквівалентних станів
[8], тобто станів з однаковими переходами під возом-дією однакових вхідних сигналів. Такі стани відповідають операторним
вершинам [1] алгоритму управління, виходи яких пов'язані з входом однієї і тієї ж вершини алгоритму.
Нехай  - розбиття безлічі А на класи
псевоеквівалентних станів. Закодуємо класи
- розбиття безлічі А на класи
псевоеквівалентних станів. Закодуємо класи 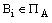 двійковими кодами K(Bi) розрядності
двійковими кодами K(Bi) розрядності
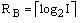
. (3)
Хай вихідна ГСА Г включає Q попарно різних наборів мікрооперацій (НМО) 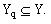 Закодуємо набір Yq двійковим кодом K(Yq) розрядності
Закодуємо набір Yq двійковим кодом K(Yq) розрядності
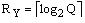
. (4)
Нехай операторна вершина bt ГСА Г відповідає стану  і нехай в ній записаний набір мікрооперацій Yq. Тоді код стану
і нехай в ній записаний набір мікрооперацій Yq. Тоді код стану 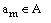 можна представити у
вигляді конкатенації код
можна представити у
вигляді конкатенації код

. (5)
Така вистава дозволяє представити автомат Мура у вигляді моделі U2 (рис.2).
Рис.2 Структурна схема автомата Мура U2
У автоматі U2 блок БФП реалізує функції (6) і блок БМО – функції (7).

(6)

(7)
При цьому елементи безлічі  використовуються для
кодування класів
використовуються для
кодування класів 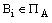 , а елементи безлічі
, а елементи безлічі 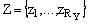 використовуються для кодування
наборів мікрооперацій.
використовуються для кодування
наборів мікрооперацій.
Пропонований підхід має ряд позитивних якостей:
- Коди класів не залежать від код мікрооперацій (і навпаки). Тому класи можна закодувати так, щоб спростити схему БМО.
- Число рядків таблиці переходів МПА U2 завжди дорівнює Н0 і не залежить від методу кодування станів.
Для кодування станів МПА U1 досить
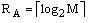
(8)
Висновок
Пропонований метод представлення код станів переходу орієнтований на зменшення
числа макровічок PAL в схемі автомата Мура. Такий підхід дозволяє зменшити число термів в системі функцій збудження пам'яті
до величини відповідного параметра еквівалентного автомата Милі. Дослідження показали, що пропонований метод завжди
ефективніший в порівнянні з класичним методом реалізації МПА Мура. При цьому число макровічок зменшується до 38%.
Зменшення числа макровічок не пов'язане з введенням додаткових блоків, що
зменшують швидкодію схеми. Більш того, зменшення числа макровічок часто супроводиться зменшенням числа рівнів схеми МПА.
При цьому підвищується швидкодія МПА і, отже, цифрової системи в цілому.
Наукова новизна запропонованого методу полягає у використанні
особливостей автомата Мура (наявність класів псевдоеквівалентних станів) для оптимізації числа макровічок PAL в логічній
схемі автомата.
Практична значущість методу полягає в зменшенні площі кристала,
займаною комбінаційною схемою МПА, що дозволяє отримати схеми, які володіють меншою вартістю, чим відомі з літератури
аналог
Подальші напрями роботи пов'язані з дослідженням можливості вживання
запропонованого методу для випадку реалізації пристрою управління в базисі FPGA, а також у складі «систем-на-крістале».
Література
- Baranov S. Logic Synthesis for Control Automata. – Kluwer Academic Publishers, 1994. – 312 pp.
- Соловьев В.В. Проектирование цифровых схем на основе программируемых логических интегральных схем. – М.:
Горячая линия - ТЕЛЕКОМ, 2001. – 636 с.
- DeMicheli G/ Synthesis and Optimization of Digital Circuits. – McGraw-Hill, 1994. – 636 pp.
- Грушницкий Р.И. Проектирование систем с использованием микросхем программируемой логики / Р.И. Грушницкий,
А.Х. Мурзаев, Е.П. Угрюмов. – СПб.: БХВ. - Петербург, 2002. –608 с.
- Maxfield C. The Design Warrior’s Guide to FPGAs. – Amsterdam: Elseveir, 2004. – 541 pp.
- Баркалов А.А. Принципы оптимизации логической схемы микропрограммного автомата Мура // Кибернетика и
системный анализ. – 1998. – № 1. – С. 65-72.
- Nababi Z. Emvedded Core Design with FPGA. – NY: McGraw-Hill, 2008, - 618pp.
- Yang S. Logic Synthesis and Optimization Benchmarks user guide. Technical report, №1991 – IWLS-UG-Saryang.-Microelectronics center of North Carolina.
- Сайт провідного виробника FPGA [Електроний ресурс] Altera
- Сайт провідного виробника CPLD [Електроний ресурс] Xilinx
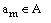 розрядності
розрядності  , для кодування станів використовуються внутрішні змінні з безлічі
, для кодування станів використовуються внутрішні змінні з безлічі
 ; as, K(as) – відповідно стан переходу і його код;
Xh – вхідний сигнал, що визначає перехід
; as, K(as) – відповідно стан переходу і його код;
Xh – вхідний сигнал, що визначає перехід 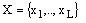 ; Фh – набір функцій збудження тригерів
пам'яті МПА, що набувають одиничного значення для перемикання пам'яті з К(am) до К(as),
; Фh – набір функцій збудження тригерів
пам'яті МПА, що набувають одиничного значення для перемикання пам'яті з К(am) до К(as),
 ; h=1,…,Н – номер переходу. У стовпці am аписується набір мікрооперацій
Yq, що формуються у стані
; h=1,…,Н – номер переходу. У стовпці am аписується набір мікрооперацій
Yq, що формуються у стані 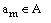 , де
, де  Ця таблиця
є основою для формування систем функцій
Ця таблиця
є основою для формування систем функцій (1)
(1) (2)
(2)
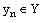 реалізується на одної макрокомірки. Для оптимального і уточненого кодування станів може бути
використаний, наприклад, відомий алгоритм ESPRESSO [3]. Проте обидва методи не можуть бути застосовані одночасно. Тому
кодування станів дозволяє оптимізувати або БФП, або БМО.
реалізується на одної макрокомірки. Для оптимального і уточненого кодування станів може бути
використаний, наприклад, відомий алгоритм ESPRESSO [3]. Проте обидва методи не можуть бути застосовані одночасно. Тому
кодування станів дозволяє оптимізувати або БФП, або БМО.
 - розбиття безлічі А на класи
псевоеквівалентних станів. Закодуємо класи
- розбиття безлічі А на класи
псевоеквівалентних станів. Закодуємо класи 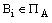 двійковими кодами K(Bi) розрядності
двійковими кодами K(Bi) розрядності
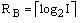 . (3)
. (3)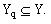 Закодуємо набір Yq двійковим кодом K(Yq) розрядності
Закодуємо набір Yq двійковим кодом K(Yq) розрядності
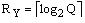 . (4)
. (4) і нехай в ній записаний набір мікрооперацій Yq. Тоді код стану
і нехай в ній записаний набір мікрооперацій Yq. Тоді код стану  . (5)
. (5)
 (6)
(6) (7)
(7) використовуються для
кодування класів
використовуються для
кодування класів 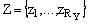 використовуються для кодування
наборів мікрооперацій.
використовуються для кодування
наборів мікрооперацій.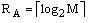 (8)
(8)