УДК 004.89
А.В. Жук, А.О. Шевченко
Донецкий национальный технический университет, г. Донецк
кафедра программного обеспечения интеллектуальных систем
ИССЛЕДОВАНИЕ ОСОБЕННОСТЕЙ СОВМЕСТНОГО ИСПОЛЬЗОВАНИЯ МЕТОДОВ ПОИСКА КРАТЧАЙШЕГО ПУТИ И СКОРОСТНЫХ ПРЕПЯТСТВИЙ ДЛЯ ОБЕСПЕЧЕНИЯ НАВИГАЦИИ АГЕНТОВ ПО КАРТЕ
Аннотация
Жук А.В., Шевченко А.О. Исследование особенностей совместного использования методов поиска кратчайшего пути и скоростных препятствий для обеспечения навигации агентов по карте. Выполнен анализ методов ограничения скоростей основанных на концепции скоростного препятствия. Рассмотрены особенности применения этих методов для навигации агентов на карте, представленной навигационной поверхностью.
Ключевые слова: поиск пути, методы ограничения скоростей, навигационная поверхность.
Постановка проблемы. Для обеспечения оптимального перемещения одного агента по карте достаточно использовать навигационные поверхности для построения кратчайшего маршрута между текущим положением агента и пунктом назначения. Однако ситуация значительно усложняется, когда на карте присутствуют как минимум два агента. В какой-то момент времени траектории их движения приведут их в одну и ту же точку карты, и возникнет необходимость в разрешении возникшего конфликта.
Метод взаимных скоростных препятствий позволяет рассчитать необходимые значения скоростей для конфликтующих агентов, и позволяет выполнить уклонение, избегая столкновения. Однако одновременное использование локального уклонения и навигации вдоль кратчайшего маршрута на карте порождает ряд задач:
- обеспечение навигации вдоль проложенного маршрута и одновременный анализ возможных коллизий;
- учёт ограничений на проходимость карты при расчёте локального уклонения;
- повторное прокладывание маршрута после выполнения локального уклонения.
Анализ литературы. Концепция скоростного препятствия [1] позволяет агенту двигаться в пространстве без коллизий. Этот метод хорошо работает, когда есть один виртуальный агент, который движется в пространстве с большим количеством движущихся препятствий. Но, к сожалению, этот метод плохо работает на группе движущихся агентов, где каждый агент активно изменяет свой вектор скорости, для того, чтобы избежать коллизии, т.к. предполагает, что другие агенты не будут менять свою скорость. Это создает колебания в движении всех агентов.
Эту проблему решает метод взаимных скоростных препятствий [2] который построен на основе концепции скоростного препятствия, но позволяет агентам решать проблему коллизий сообща, т.е. каждый из агентов выполняет часть маневра уклонения, допуская, что оставшуюся часть выполнит другой агент.
При использовании этого метода, для маневра уклонения, агенты автоматически выбирают одинаковую сторону, что позволяет им благополучно обойти друг друга. Но если вектор скорости агента будет сильно отличаться от вектора, указывающего в точку назначения, агенты могут выбрать разные стороны для маневра, что приведет к проблеме названной «взаимные танцы»[3]. При ее проявлении агенты могут оказаться заблокированными на карте на продолжительное время.
«Взаимные танцы» решает метод гибридных взаимных скоростных препятствий [4], который заставляет агентов выбирать постоянно одну и ту же сторону для маневра уклонения.
Навигационная поверхность – все проходимое пространство карты, состоящее из непересекающихся полигонов. Навигационная поверхность может содержать дополнительную информацию. Например: стоимость прохода, или условия прохода для определенных классов юнитов. Строить пути по ней можно используя центра полигонов, грани, точки полигонов, либо несколько этих методов одновременно [5]. Но все равно итоговый путь не будет оптимальным. Для создания оптимального пути применяют сглаживание пути. Метод прост: если следующая точка пути  видна из текущей точки
видна из текущей точки 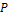 , то точка
, то точка 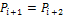 .
.
В сравнении с более простыми методами построения пути, такими как вейпоинты или разбиение карты на сетку, навигационная поверхность обеспечивает построение самого короткого пути для агента.
Цель статьи – рассмотреть особенности применения методов взаимных скоростных препятствий для обеспечения локальных уклонений агентов при следовании по маршруту по карте, представленной навигационной поверхностью.
Обеспечение навигации вдоль проложенного маршрута и одновременный анализ возможных коллизий. Пусть кратчайший маршрут длинной N представляет собой последовательность точек:
 , (1)
, (1)
где  – начальная точка маршрута,
– начальная точка маршрута,
 – промежуточные точки маршрута,
– промежуточные точки маршрута,
 – конечная точка маршрута.
– конечная точка маршрута.
При перемещении по маршруту агент в каждый момент времени должен двигаться со скоростью:
 , (2)
, (2)
где i – индекс последней пройденной агентом точки маршрута,
 – величина скорости движения агента,
– величина скорости движения агента,
 – операция нормирования вектора.
– операция нормирования вектора.
Метод взаимных скоростных препятствий не учитывает данные о пункте назначения движения агента. Входными данными являются:
- требуемый вектор скорости для каждого из агентов (
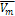 );
); - текущий вектор скорости каждого из агентов (
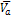 ).
).
Результатом применения метода является новый текущий вектор скорости для каждого из агентов. Очевидно, что для продолжения движения по намеченному маршруту, требуемый вектор скорости  необходимо пересчитывать в каждый момент времени:
необходимо пересчитывать в каждый момент времени:
 , (3)
, (3)
где 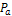 – текущая позиция агента на карте.
– текущая позиция агента на карте.
Описанная ситуация с векторами скоростей приведена на риc. 1.
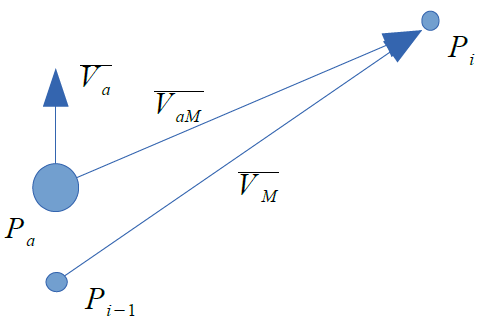
Рисунок 1 – Расчёт вектора скорости движения агента при совместном использовании методов поиска кратчайшего пути и метода взаимных скоростных ограничений для навигации по карте
Учёт ограничений на проходимость карты при расчёте локального уклонения. Маршрут M прокладывается таким образом, что движущийся по нему агент может касаться препятствий, но траектория его движения всегда находится в пределах проходимой области карты.
В то же время, при выполнении локального уклонения направление движения может быть выбран таким образом, что после выполнения маневра агент выйдет за границы области проходимости.
Метод взаимных скоростных препятствий позволяет рассчитать для агента вектор скорости, гарантирующий отсутствие столкновений с препятствиями. Таким образом, если представить границы областей проходимости на карте как препятствия для метода взаимных скоростных препятствий, то рассматриваемая проблема будет решена.
Каждый из полигонов навигационной поверхности можно разбить на непересекающиеся треугольники так, что их суммарная площадь будет равна площади полигона. Разбиение всех полигонов навигационной поверхности на треугольники будем называть триангуляцией навигационной поверхности. Пример навигационной поверхности и её триангуляции представлены на риc 2.
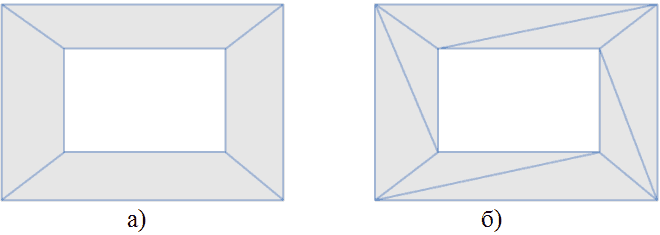
Рисунок 2 – Навигационная поверхность (а) и её триангуляция (б). Закрашенные области соответствуют проходимым участкам карты
Каждый из K полученных треугольников представляет собой полный граф. Если все эти треугольники объединить в один граф, то получим граф, состоящий K компонент связности. Если в этом графе объединить вершины, имеющие одинаковые координаты, то получим связный граф с кратными ребрами. Пусть в получившемся графе K вершин и пусть M – матрица смежности этого графа. Если над матрицей M выполнить следующую операцию
 , (4)
, (4)
то это будет соответствовать удалению в полученном графе всех кратных ребер. Полученный граф будет содержать только компоненты связности, каждая из которых будет циклом – контуром одной из границ непроходимых областей на карте.
Повторное прокладывание маршрута после выполнения локального уклонения. Одним из свойств маршрута, проложенного по навигационной поверхности, является то, что каждые две соседние точки в нем находятся в прямой видимости друг от друга, т.е. в контурах границ нет ребра, которое пересек бы отрезок  .
.
Как обсуждалось ранее, после выполнения локального уклонения вектор скорости агента к следующей точке пути будет нуждаться в пересчёте. Однако не исключено, что после уклонения в контурах границ найдётся ребро, с которым пересечется отрезок  . Наличие такого отрезка будем считать показателем необходимости повторного расчёта маршрута из точки
. Наличие такого отрезка будем считать показателем необходимости повторного расчёта маршрута из точки 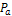 в точку E.
в точку E.
Выводы. В данной работе рассмотрен ряд задач, решение которых позволило применять метод взаимных скоростных препятствий для обеспечения локальных уклонений агентов при следовании по маршруту по карте, представленной навигационной поверхностью.
Список литературы
- Fiorini P. Motion planning in dynamic environments using velocity obstacles / P. Fiorini, Z. Shiller – Int. Journal of Robotics Research, vol. 17, no. 7, 1998. – 760-772 c.
- Van den Berg J. Reciprocal Velocity Obstacles for real-time multi-agent navigation / J. Van den Berg, M. Lin, D. Manocha – IEEE Int. Conf. on Robotics and Automation, 2008. – 1928-1935 с.
- Snape J. Reciprocal collision avoidance and navigation for video games / J. Snape – Game Developers Conf., 2012.
- Snape J. The Hybrid Reciprocal Velocity Obstacle / J. Snape, J. Van den Berg, S. J. Guy, D. Manocha – IEEE Transactions on Robotics, v.27 n.4, 2011. – 696-706 c.
- Kallmann M. Shortest paths with arbitrary clearance from navigation meshes / M. Kallmann – Proceedings of the Eurographics SIGGRAPH Symposium on Computer Animation, 2010.