Содержание

1. Введение
2. Цель и задачи
3. Описание задачи картографирования
   1. Представление мира
   2. Алгоритм картографирования
   3. Инвертированная модель измерения
   4. Зависимость значения занятости от расстояния до объекта
4. Заключение
5. Список использованных источников

Введение

В современном виде робототехника формировалась в середине прошлого века, прежде всего благодаря развитию цифровой вычислительной техники. Потребность в роботах возникла из-за необходимости в помощи либо замене человека в среде, которая опасна для него либо недоступна, а также по экономическим соображениям [1].

Для мобильных роботов, используемых на предприятиях и в быту, может быть необходимо иметь карту среды, в которой они будут действовать. Карта может строится другим устройством или человеком. Однако для того, чтобы робот смог построить точную карту, ему также необходимо точно определять собственное положение на создаваемой карте. Таким образом, возникает трудность, часто именуемая проблемой курицы и яйца: для локализации робота необходимо иметь карту, но и для построения карты необходимо знать состояние и измерения робота. Для решения этой задачи используются методы SLAM.

SLAM (Simultaneous Localization and Mapping — одновременная локализация и картографирование) — название методов, позволяющих автономному транспорту создавать карту и одновременно определять свое местоположение на ней. Это делает возможными для мобильного робота, помещенного в неизвестное место неизвестной среды, ее картографирование и навигацию в ней. Большое количество исследований, предлагающих новые решения задач SLAM, а также снижение стоимости датчиков и контроллеров вместе с ростом вычислительных способностей последних привели к широкому внедрению SLAM в проекты мобильных роботов [2, 3].

Нахождение позиции робота по точным результатам сканирования и точной карте не является слишком сложной задачей [4, 5]. Хоть такие алгоритмы и просты в вычислительном плане, в реальных задачах постоянное получение точной информации практически невозможно.

При работе с картой среды и ее картографированию важно учитывать существование высокой неопределенности, заключающейся в следующем:

• непредсказуемость окружающего мира. На испытательных полигонах или любых других хорошо контролируемых средах этот пункт может быть минимизирован, однако жилые дома, офисы, улицы характеризуются высокой динамичностью как минимум из-за деятельности людей;
• особенности работы датчиков. Хорошим примером будет наличие неточностей в результатах измерений дальномеров, которые определяют дистанцию с некоторой ошибкой, могут не обнаружить объект, дать неверный результат при воздействии шумов, выйти из строя;
• неточность определения положения устройства, проводящего измерения, если оно необходимо для картографирования;
• использование приближенных и упрощенных математических моделей, алгоритмов.

Необходимость учета неопределенностей привела к развитию и распространению вероятностной робототехники. Согласно ее представлениям, используемые модели неполны и недостаточны точны для осуществления управления, равно как и показания датчиков, что приводит к комбинированию модели и результатов работы сенсоров с применением методов статистики [6].

Работа посвящена разработке универсального решения картографирования помещений, не зависящее от реализации устройства-источника: за счет конструктора принимаемых данных происходит абстрагирование от деталей реализации и работы источника. Пользователю достаточно знать только структуру данных и иметь представление о параметрах используемых дальномеров. Создание карты может быть как самостоятельной задачей, так и использоваться как часть SLAM.

1. Цель и задачи

Целью выпускной работы является разработка универсального решения картографирования помещений. Для достижения цели необходимо решение следующих задач:

• изучение предметной области;
• разработка математической модели процесса картографирования;
• разработка конструктора принимаемых данных;
• разработка пользовательского интерфейса.

2. Описание задачи картографирования

Двумерная метрическая карта представляет собой равномерную двумерную сетку, на которой распределены случайные бинарные переменные, отображающие состояние занятости соответствующего местоположения. Алгоритмы картографирования реализуют приблизительную апостериорную оценку для этих случайных переменных. На рисунке 1 показана графическая модель картографирования с известными местоположениями и измерениями [6].

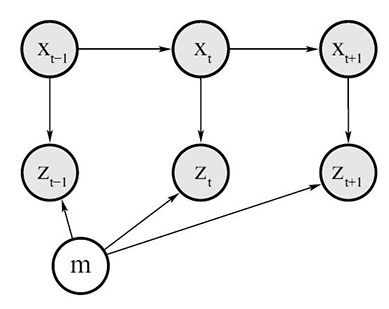
X = {x_0:t} — включает информацию о местоположении устройства с начала его работы до текущего момента t

Z = {z_0:t} — выполненные измерения.

m = {m_i} — карта, состоящая из ячеек m_i

Задача картографирования состоит в том, чтобы построить карту m, зная состояния устройства X и измерения датчиков Z. Датчиками обычно выступают дальномеры.

2.1. Представление мира

Сканируемый мир представляется двумерной дискретной метрической картой занятости. Информация о внешней среде хранится в виде ячеек, значение которых отображает вероятности занятости пространства. Одна ячейка карты соответствует определенной площади пространства.

Пример карты, построенной с помощью одного скана, показан на рисунке 2. Светлые ячейки — свободное пространство, темные — занятое, темно-серые (средняя яркость) — неизвестное состояние ячейки.

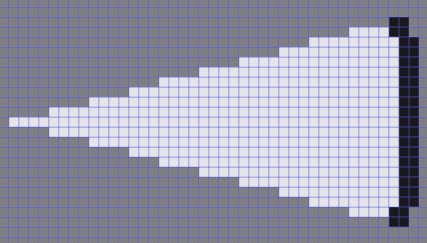
Данный тип карты был предложен Элфесом и Моравеком в середине 1980-х и приобрел большую популярность за счет своей надежности, простоты в реализации и возможности использования с сильно зашумленными измерениями [7, 8]. Карта занятости отлично подходит для представления двумерного изображения помещения за счет ее высокого разрешения, однако очевидным недостатком выступает занимаемый в памяти большой размер карты [9, 10].

Приняты следующие часто используемые допущения:

1. Представляемое пространство, как и ячейка карты, может быть либо полностью занято, либо полностью свободно. Для лучшего понимания можно описать следующую ситуацию: пусть размер ячейки карты соответствует 10 см2, обнаруженное препятствие реального мира в горизонтальной плоскости имеет площадь 1 см². Препятствие в 10 раз меньше соответствующего ячейке карты размера, однако занятой считается вся ячейка, то есть 10 см² пространства.
2. Состояние каждой ячейки бинарно, то есть она либо свободна, либо занята.
3. Вероятности занятости клеток независимы друг от друга. В реальности занятости соседних клеток часто связаны. Например, если определяемая клетка карты является частью стены, то соседние клетки с высокой вероятностью будут также заняты. Однако это позволяет сильно упростить модель,
4. Окружение статично. Предположение о статичности также упрощает построение карты. В некоторых случаях окружающая среда действительно не отличается изменениями, однако, например, сервисные роботы нередко предназначены именно что для работы среди людей, то есть в динамической среде, изменчивой.

2.2. Алгоритм картографирования

Стандартом алгоритма картографирования с использованием сеток занятости является вычисление апостериорного распределения по карте на основе имеющихся данных:

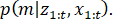
Каждая ячейка карты представляется бинарной случайной величиной, отражающей вероятность занятости ячейки:

• p(m_i) = 1 — ячейка mi занята;
• p(m_i) = 0 — ячейка mi свободна;
• p(m_i) = 0,5 — состояние ячейки m_i неизвестно.

Принятое ранее допущение 2 позволяет разбить задачу оценки карты, состоящей из большого множества ячеек, на отдельные оценки каждой ячейки:

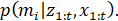
Благодаря этому, апостериорное распределение по всем картам аппроксимируется в виде произведения маргиналов:

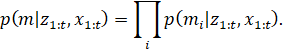
Декомпозиция делает оценку вероятности занятости для каждой клетки карты бинарной задачей со статическим состоянием. Для ее решения используются понятия теории вероятностей, байесовский фильтр и свойства Маркова.

По теореме Байеса:

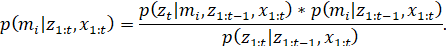
Используя ранее обозначенные понятия и допущения, выполнив переход от вероятностей занятости к отношениям шансов, формула (4) преобразуется к следующему виду:

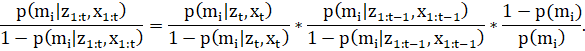
В правой части уравнения (5) выделяются три множителя:

1. Первый множить соответствует текущему измерению и состоянию устройства (время t); новая информация.
2. Второй множитель отражает оценку всех прошлых моментов времени; рекурсивный член.
3. Третий множитель — априорная вероятность состояния m_i.

Однако уравнение (5) в текущем виде определяет не вероятность p(m_i), а отношение шансов. Для получения вероятности занятости ячейки выполняется приведение к следующему виду:

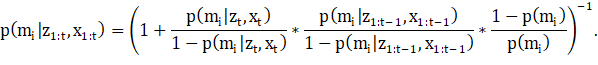
Полученная формула (6) характеризуется сложными вычислениями, которые могут быть упрощены. С целью повышения эффективности вычислений для уравнения (5) применяется нотация логарифмов отношения шансов.

Известно, шансы некоторого состояния a определяются в виде отношения вероятности данного события и вероятности его противоположности. Логарифм шансов имеет вид:

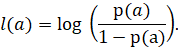
Восстановление осуществляется следующим способом:

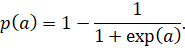
Логарифм шансов принимается значения от -∞ до +∞. В этой нотации Фильтр Байеса имеет лаконичный вид и обходит проблему отсекания вероятностей, близких к 0 или 1.

Выполним преобразования членов уравнения (5) согласно описанной нотации:

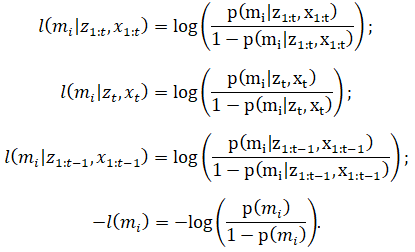
Подставим полученные в (9) преобразования в (5):

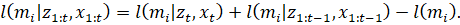
Приведение к логарифмическому виду заменило умножение дробей на сложение значений логарифмов, ускоряя тем самым вычисления. Также преимуществом является возможность избежать численной нестабильности для вероятностей вблизи нуля или единицы.

При использовании логарифмического подхода в памяти устройства карта будет хранить значения ячеек и выполнять необходимые для ее обновления вычисления в логарифмической форме. Для визуализации карты необходимо выполнить обратное преобразование по формуле (8).

Формулу (10) можно представить в кратком виде:

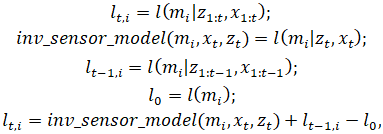
где l_t,i — логарифм отношения шансов, что ячейка m_i карты M в момент t имеет препятствие;

inv_sensor_model(m_i,x_t,z_t) — инвертированная модель сенсора;

l_t-1,i — рекурсивный член;

l₀ — априорная часть, логарифм шансов начальной оценки.

Итоговый алгоритм картографирования показан на рисунке 3.

Алгоритм картографирования, показанный на рисунке 3, проходит по всем клеткам карты M и обновляет те ячейки, что попадают в поле измерения датчика.

2.3. Инвертированная модель измерения

В описываемых ранее уравнениях используется инвертированная модель сенсора p(m_i|x_t,z_t) вместо прямой p(z_t|x_t,m_i). Модель называется инвертированной потому, что построение карты выполняется по измеренным датчиком расстояниям, причиной которых в действительности является сама карта. На рисунке 4 показан пример измерения обратной моделью датчика, где яркость ячеек соответствует вероятности занятости; также обозначены некоторые параметры модели.

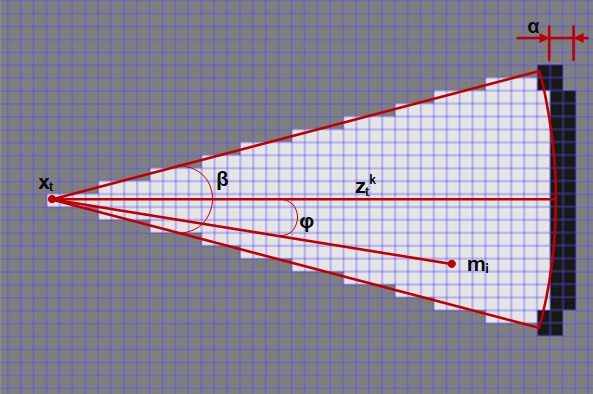
Алгоритм сканирования согласно обратной модели датчика, пример которого на рисунке 4, показан на рисунке 5. Использованы следующие обозначения:

• x, y — координаты устройства;
• θ — глобальное направление ориентации;
• α — толщина препятствия;
• β — ширина луча сенсора;
• l_occ, l_free — значения занятости и свободности клетки в форме логарифма шансов;
• k — индекс луча;
• z_max — максимальная дистанция работы дальномера.

Описанный алгоритм задает всем ячейкам в конусе измерений, расстояние до которых близко к данным измерения, значение занятости l_occ.

Первоначально в строках 4–6 определяется индекс луча k, угол φ и расстояние r до центра m_i.

В строке 8 возвращается значение априорной вероятности l₀, если дальность до рассматриваемой ячейки превышает максимальную рабочую дальность датчика z_max или находится дальше чем на α/2 измеренного расстояния z_t^k, симулируя во втором случае отсутствие видимости за препятствиями.

В строке 10 возвращается l_occ, если дальность до клетки находится в диапазоне z_t^k ± α/2.

Значение l_free < l₀ возвращается в строке 12, если дальность до клетки меньше измеренного расстояния z_t^k.

2.4. Зависимость значения занятости от расстояния до объекта

Возможная зависимость (в форме вероятности) для ультразвукового датчика показана на рисунке 6.

Вероятность занятости клетки зависит от расстояния до измеренного объекта z и чисел d₁, d₂, d₃, d₄. Клетки до точки 1 свободны (значение p_free), так как находятся перед препятствием. Участки 1–2 и 2–3 подразумевают неточность измерений относительно z. 3–4 — представление толщины препятствий и имеют значение занятости p_occ. 4–5 — все еще некоторая неточность, а начиная с точки 5 считается, что клетки за препятствием, следовательно их состояние неизвестно и они имеют значение априорной вероятности p₀.

Лазерные дальномеры обладают более простой моделью, так как имеют большую точность и разрешающую способность. Вид модели для лазерных дальномеров показан на рисунке 7.

Считая измерения лидара достаточно точными, до дистанции z-d₁ клетки карты принимаются свободными, а после z+d₂ — находящимися за препятствиями, следовательно имеющими априорную вероятность занятости. Препятствие находится в диапазоне от z-d₁ до z+d₂.

Заключение

В данной работе рассмотрена задача картографирования на основе поступаемые данных с источника. Считается, что данные о состоянии устройства и результатах его измерений известны, и на их основе обходимо выполнить построение карты. Также описаны допущения, часто принимающиеся для решения задачи.

Приведено математическое описание решения задачи и пример алгоритма на псевдокоде.

Описана инвертированная модель измерения датчиков и алгоритм процесса ее измерения на псевдокоде. Модель называется инвертированной потому, что построение карты выполняется по измеренным датчиком расстояниям, причиной которых в действительности является сама карта, то есть среда.

Показаны зависимости значений занятости от измеренного расстояния для сонара и лидара. Лазерные дальномеры точнее сонаров и менее подвержены шумам, что позволяет оценивать состояние ячеек карты с большей уверенностью в их занятости или свободности и точностью, используя при этом более простые модели.

На момент написания реферата выполнено написание и тестирование программной модели задачи картографирования, описанной в данной работе.

Список использованных источников

1. Юревич, Е. И. Основы робототехники : учебное пособие / Е. И. Юревич. – Текст : электронный // ЭБ СПбПУ. – 2-е изд. – URL: http://elib.spbstu.ru/dl/325.pdf.
2. SLAM (Simultaneous Localization and Mapping). – Text : electronic // MathWorks. – URL: https://www.mathworks.com/discovery/slam.html.
3. Durrant-Whyte, H. Simultaneous localization and mapping: part I / H. Durrant-Whyte, T. Bailey. – Text : electronic // IEEE Robotics & Automation Magazine. – 2006. – № 13. – pp. 99-110. – URL: https://ieeexplore.ieee.org/document/1638022.
4. Krekov, O. I. 2D indoor position estimation method for a mobile robot / O. I. Krekov, T. V. Zavadskaya, Ye. N. Kushnirenko. – Text : electronic // Young scientists' researches and achievements in science. – Donetsk : DonNTU, 2024. – pp. 197-203.
5. Завадская, Т. В. Определение позиции робота по сформированной двумерной карте помещения / Т. В. Завадская, О. И. Креков. – Текст : электронный // Информатика и кибернетика. – Донецк : Доннту, 2023. – №4 (34). – с. 12-18. – URL: https://infcyb.donntu.ru/IC_34.pdf.
6. Thrun, S. Probabilistic Robotics / S. Thrun, W. Burgard, D. Fox. – 2005. – p. 672.
7. Moravec, H. P. High resolution maps from wide angle sonar / H. P. Moravec, A. Elfes. – Text : electronic // Proceedings. 1985 IEEE International Conference on Robotics and Automation. – 1985. – pp. 116-121. – URL: https://www.ri.cmu.edu/pub_files/pub4/moravec_hans_1985_1/moravec_hans_1985_1.pdf.
8. Elfes, A. Using Occupancy Grids for Mobile Robot Perception and Navigation / A. Elfes. – Text : electronic // Computers. – 1989. – vol. 22, no. 6. – pp. 46-57. – URL: https://www.researchgate.net/publication/2953854_Using_Occupancy_Grids_for_Mobile_Robot_Perception_and_Navigation.
9. Thrun, S. Robotic Mapping: A Survey / S. Thrun. – Text : electronic // Stanford University. – 2002. – URL: http://robots.stanford.edu/papers/thrun.mapping-tr.pdf.
10. Thrun, S. Learning Occupancy Grid Maps With Forward Sensor Models / S. Thrun. – Text : electronic // Stanford University. – 2003. – URL: http://robots.stanford.edu/papers/thrun.occ-journal.pdf.