| Биография |
ДонНТУ >
Портал магистров ДонНТУ |
| Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание | |
Контекстное моделирование
Общие сведения
Контекстное моделирование основано на том, что элементы изображения не являются независимыми, а влияют друг на друга.
Пусть уже закодированы или декодированы элементы с номерами 1, 2, ..., i-1 и происходит определение распределения вероятностей i-го элемента. Оно происходит с учетом значений нескольких наиболее сильно влияющих на него предыдущих элементов или величин, вычисленных по ним. Набор параметров, найденных по уже обработанной части изображения и используемых при определении распределения данного элемента называется его контекстом. Само использование контекста называется контекстным моделированием.
Применение контекстного моделирования к изображению
Для текстовых или произвольных двоичных файлов элементом обычно является байт, слово или двойное слово и контекстом являются несколько предыдущих элементов. Для каждого набора предыдущих элементов хранятся вероятности различных значений одного последующего элемента. Обычно эти вероятности находятся или уточняются по мере кодирования или декодирования. Также по мере продвижения по файлу увеличивается длина используемого контекста. При этом хранение всех вероятностей даже при длинных контекстах не требует очень много памяти, т.к. из всех возможных сочетаний соседних элементов в файле встречается лишь незначительная часть.
Контекстное моделирование для полноцветных изображений имеет свои особенности:
- Хранить вероятности для всех возможных контекстов даже из 3 пикселей невозможно, т.к. в реальных изображениях могут встретиться все их сочетания и потребуется слишком много памяти.
- Для обычных двоичных файлов изменение даже одного бита в контексте полностью меняет распределение рассматриваемого элемента. Для изображений (и других оцифрованных аналоговых данных) незначительные изменения в контексте приводят к незначительным изменениям в распределении рассматриваемого элемента.
- Построение распределений для различных контекстов во время обработки изображения даст не очень точный результат, т.к. их число слишком велико по сравнению с объемом статистических данных, которые можно получить из одного изображения и таких данных не хватит для достаточно точного прогнозирования вероятностей.
- Существуют глобальные закономерности, общие для всех полноцветных изображений. Распределения при некотором контексте для различных изображений отличаются в основном из-за особенностей изображений, которые можно выразить количественно (степень зашумленности, корреляция между цветовыми компонентами, и. т. д.).
Из пунктов 1 и 2 следует, что целесообразно объединять группы схожих контекстов в один контекст, что позволит резко уменьшить затраты памяти. Из пунктов 3 и 4 следует, что можно найти распределения при всех контекстах сразу для всех возможных изображений, а при кодировании конкретного изображения использовать их с учетом статистических величин, вычисленных по данному изображению. Это позволит использовать многие из имеющихся контекстных зависимостей и точнее предсказывать распределения. Именно этот подход применяется в разработанном алгоритме. С другой стороны, при таком подходе увеличивается размер программы кодирования/декодирования, т. к. с ней будет поставляться база данных с распределениями значений элементов изображения. Это также делает алгоритм более специализированным, т. е. он более эффективно сжимает изображения сходные с теми, которые участвовали в построении распределений и менее эффективно - остальные.
Дерево контекстов
Будем объединять несколько контекстов с близкими параметрами и распределением случайной величины в одну группу. При этом будем считать, что все величины, имеющие контекст, принадлежащий к данной группе, имеют одно и то же распределение, относящееся к этой группе. Группы не пересекаются и полностью покрывают все возможные контексты. Распределение для каждой группы определим как распределение вероятностей значений всех случайных величин, которые имеют контекст, относящийся к этой группе.
Очевидно, что чем больше групп контекстов взять, тем точнее будет предсказание распределения. Однако база данных не должна занимать слишком много места. Можно сформулировать следующую задачу: найти способ так сгруппировать контексты, чтобы получить не более N групп и при этом точность предсказания по этим группам была бы максимальной. Кроме того, представление этих групп должно позволять быстро по конкретному контексту находить соответствующую группу и распределение.
Точное решение этой задачи невозможно, т.к. потребует перебора слишком многих вариантов.
Мной был разработан и реализован метод, дающий приближенное решение. Уже после завершения работы над алгоритмом сжатия изображений я обнаружил, что подобный подход применяется при аппроксимации многомерных функций. Однако, мне не известно о применении такого подхода в существующих алгоритмах сжатия изображений.
Для определения и хранения групп контекстов используется бинарное дерево. Листья и остальные узлы отличаются по структуре. Пусть в контекст входят Z величин, i-я из них может иметь значение от X0i до Y0i. При движении по дереву от корня к листьям для каждого i-го параметра из контекста будем хранить текущий диапазон его значений в виде пары Xi, Yi. В корне дерева эти диапазоны равны максимально возможным, т.е. Xi=X0i, Yi=Y0i, 1≤i≤Z. В каждом узле, не являющемся листом хранится номер параметра контекста z, по которому производится расщепление множества контекстов на 2 подмножества и ссылки на правого и левого детей. У обоих детей Xi и Yi совпадают с Xi и Yi родителя для всех i, не равных z. Для i=z у левого ребенка XLz=Xz, YLz=(Xz+Yz)/2, а у правого ребенка XRz=(Xz+Yz)/2+1, YRz=Yz. Таким образом, при переходе от любого узла к его детям происходит деление текущего множества контекстов на 2 равновеликих подмножества, не пересекающихся и полностью покрывающих исходное.
В листьях не содержится ссылок на детей. Там содержатся 3Z распределений в табличном виде, в которых накапливаются количества различных значений всех величин, попадающих в соответствии со свом контекстом в данный лист дерева. Обозначим их как L[1..Z], R[1..Z] и ALL[1..Z]. Пусть значения верхней и нижней границ i-го параметра контекста для текущего листа есть Xi и Yi, а значение i-го параметра контекста для рассматриваемого в настоящий момент элемента изображения есть Vi. В распределение L[j] попадают те значения случайной величины, для которых Vj≤(Xj+Yj)/2, а в R[i] - для которых Vj>(Xj+Yj)/2. При попадании в лист очередного значения единица добавляется к соответствующему значению либо R[i], либо L[i] для всех i от 1 до Z. В распределении ALL[i] содержатся частоты всех величин, попадающих в лист. ALL представлен массивом, а не одним распределением в связи с предсказанием наиболее вероятного значения, которое описано ниже. На рисунке изображен один узел дерева.
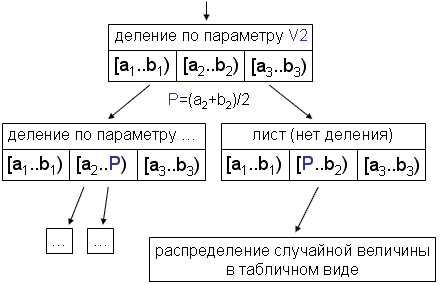
Через каждые K добавлений происходит оценка экономии места, которую может дать расщепление данного листа по одному из параметров контекста. Для этого оценивается суммарный объем памяти, который заняли бы после сжатия все элементы распределений ALL[i], L[i] и R[i]. Оценка осуществляется по формуле, где v1 и v2 - минимальное и максимальное возможные значения величины, Kj - число величин, имеющих значение j, K - общее число величин, учтенных в данном распределении. Если для некоторого i S(ALL[i])*P>S(L[i])+S(R[i])+S0, то происходит расщепление по i-му параметру, текущий лист превращается в рядовой узел, а его детьми становятся 2 листа с распределениями, заполненными 0.
Чем больше величина S0, тем реже происходят расщепления листьев, но тем точнее выбирается параметр, по которому нужно расщепить. P задает минимальную экономию памяти, при которой имеет смысл расщеплять лист. В начале дерево состоит из одного листа. Далее в него добавляются значения с контекстами, полученные из обработки большого числа изображений. Алгоритм останавливается, как только число листьев достигает N.
При кодировании и декодировании дерево хранится в виде массива ссылок, по которому можно узнать нужное распределение за O(log2H), где H - средняя высота дерева.
Полученный набор групп контекстов обладает следующими достоинствами:
- Легко представим в памяти (например, деревом) и возможен быстрый поиск нужного распределения по его контексту.
- По параметрам, которые сильнее влияют на распределение, происходит больше расщеплений, чем по малозначительным, т.е. они будут сильней влиять на величину и после объединения контекстов в группы. По параметрам, не влияющим на распределение, не будет происходить расщеплений.
- Если в некоторой группе контекстов распределения очень разнятся и нужно было бы разделить ее на подгруппы, но при этом лишь малое число величин имеют такой контекст, то деления не произойдет. Если же в некоторую группу контекстов попадают очень много величин, то даже при незначительных различиях распределений эта группа будет разделена. Это хорошо отвечает критерию минимального размера файлов после сжатия.
После нахождения всех групп происходит еще один проход по множеству изображений и для каждой группы строится свое распределение, которое и будет сохранено в базу данных.
Такой набор распределений строится для каждого типа элементов изображений. Всего при волновом преобразовании изображения в разработанном алгоритме выделяются 6 типов элементов - по 2 на каждую цветовую компоненту.
На краях изображений невозможно построить такой же контекст, как и для элементов в центре. С другой стороны, краевых элементов изображения мало и их суммарный вклад в объем файла небольшой. Поэтому для них строятся свои деревья контекстов меньшего размера, обеспечивающие меньшую точность.
Все деревья контекстов можно строить одновременно и прервать выполнение алгоритма когда общее число их листьев достигнет N. Таким образом, под базу данных для элементов, которые трудней предсказать, будет отведено меньше места и за счет этого можно будет сохранить больше информации об элементах, которые можно предсказать точней. При одинаковом общем объеме всех данных такой подход позволяет сохранить больше полезной информации, чем выделение под все базы данных распределений фиксированного места.
Эксперименты показали, что все распределения элементов массивов, полученных при волновом преобразовании, имеют одно наиболее вероятное значение. Вероятность значений резко уменьшается при удалении от наиболее вероятного. Это значение находится в линейной зависимости от соседних элементов изображения.
Если вычислять наиболее вероятное значение по соседним элементам, а затем кодировать не значение текущего элемента, а разность реального и наиболее вероятного значений, то можно существенно увеличить степень сжатия. Поэтому и при построении дерева контекстов и при нахождении самих распределений сначала собираются данные для нахождения линейной зависимости текущего элемента от соседних, затем она находится по МНК, а лишь затем происходит накопление значений вероятностей в массивах.
Читать дальше: Цветовое пространство| Биография |
ДонНТУ >
Портал магистров ДонНТУ |
| Реферат | Библиотека | Ссылки | Отчет о поиске | Индивидуальное задание | |