Автореферат
Постановка задачи
Сварка - технологический процесс, широко применяемый во всех отраслях для изготовления новых и ремонта
эксплуатируемых механизмов, конструкций и оборудования.
В последние годы быстро развивается автоматизации дуговой сварки (сварка плавлением) с применением
промышленных роботов, которая может применяться во всех отраслях при изготовлении металлоконструкций.
Сваркой плавлением можно соединять практически все используемые для изготовления конструкций металлы
и сплавы любой толщины. Этот процесс очень вреден для человека, связан с сильным шумом, большими
температурами, воздействием дыма и интенсивного света (искрение), автоматизация обеспечивает высокое
качество швов, большую стабильность и скорость работы.
Роботы, применяемые для автоматизации дуговой сварки, представляют собой универсальные перепрограммируемые
манипуляторы. Система управления сварочным роботом должна обеспечивать быструю настройку параметров
управления для заданной траектории движения сварочной горелки, которая может быть задана аналитически
функцией перемещения горелки во времени или задана оператором множеством точек, которые могут быть получены
экспериментально. Во время сварки оператор должен иметь возможность подкорректировать траекторию, чтобы
обеспечить точность позиционирования не более необходимой - ±0.1мм. Также необходимо учитывать типы материалов
свариваемых изделий и их толщину, от которых будет зависеть скорость перемещения головки сварочной горелки.
Если скорость горелки будет отличаться от заданной, то не будет обеспечено высокое качество швов, даже при
нулевой ошибке позиционирования. Т.к. меньшая скорость достаточно не расплавит края свариваемых материалов,
а большая - наоборот переплавит их.
Основной проблемой управления дуговой сваркой является проблема точного позиционирования, т.е. точного
отслеживания заданной траектории в пространстве и во времени, при непрерывном контурном управлении для
выполнения относительно сложных манипуляционных задач. Основными факторами, порождающими эту проблему,
является существенная нелинейность динамической и кинематической модели, динамическая взаимосвязь между
отдельными системами, а также незапланированные факторы: изменение программы траектории или неожиданное
изменение полезной нагрузки.
Большинство ранее применяемых методов управления либо не учитывали изменение динамики во времени, либо
были настолько сложные и громоздкие в вычислительном отношении, что требовали очень большого количества
вычислений на каждом шаге за короткий промежуток времени. В первом случае не обеспечивались заданные
требования к динамическому регулированию, а во втором - приводило к необходимости использования очень
мощных и дорогих контролеров.
Для устранения проблем нелинейностей дифференциальных уравнений применяется линеаризация динамической
модели. Линеаризация с помощью классических методов с использованием разложения нелинейных дифференциальных
уравнений в ряд Тейлора в окрестности рабочей точки нуждается в перенастройке параметров управления при
изменении рабочей точки.
Для устранения этих же проблем можно применить новый общий метод компенсации взаимосвязей и нелинейностей
дифференциальных уравнений динамики с использованием диффеоморфного преобразования и теории алгебры Ли.
Данный подход основан на идее получения "внешней линеаризации" сложной нелинейной системы с использованием
диффеоморфного преобразования координат и нелинейной обратной связи по состоянию. Этот метод позволяет
обеспечить поблочную развязку выхода; конструктивный алгоритм нахождения нелинейной обратной связи для
подсистем, в которых число выходов может быть меньше или равно числу входов; развязку выходов нелинейной
обратной связью с точки зрения состояния системы; для обеспечения устойчивости системы управления нелинейная
обратная связь соединяется с контролером оптимальной коррекции ошибок.
Преимуществом этого метода является то, что параметры управления не нуждаются в пере настройке, поскольку
линеаризация проводится не в конкретной точке, а на целом подмножестве нелинейных плоскостей.
Вверх
1. АНАЛИЗ СУЩЕСТВУЮЩИХ АЛГОРИТМОВ УПРАВЛЕНИЯ МАНИПУЛЯЦИОННЫМИ ПРОМЫШЛЕННЫМИ РОБОТАМИ.
1.1. Анализ существующих методов синтеза алгоритмов управления манипуляционным промышленным роботом.
Планирование траектории движения манипулятора промышленного робота осуществляется с помощью алгоритмов управления
планированием. Эти алгоритмы управления рассматриваются как нелинейные алгоритмы разделения командного движения
по степеням подвижности манипулятора. Их реализация связана с решением нелинейных уравнений, характеризующих
конфигурацию механизма при заданном положении рабочих органов промышленных роботов. Для решения таких нелинейных
задач прибегают либо к помощи ЭВМ, либо имитационному моделированию с использованием реальных моделей манипуляционных
систем.
Для линеаризации уравнений, описывающих поведение манипуляционной системы при малых изменениях координат элементов
механизма, обычно прибегают к дифференцированию по времени координат положения звеньев в сложном механизме,
связанном нелинейными зависимостями либо к компенсации нелинейностей и взаимодействии при помощи регуляторов и
обратной связи.
Задачей управления является выработка алгоритма требуемого функционирования приводов манипулятора. При этом используется
несколько методов управления планированием траектории движения манипулятора промышленного робота.
Метод управления по вектору скорости состоит в задании скорости движения рабочих органов манипуляционной
системы в виде шестимерного вектора, представляющего проекции векторов угловой скорости рабочего органа и
скорости его некоторой точки в какой-либо системе координат, которые предусматриваются алгоритмами управления
таким образом, чтобы полностью определить скорость рабочего органа в текущей точке траектории.
Непосредственное использование этого решения для целей управления ограничиваются возникновением в процессе
управления вырожденных конфигураций механизма, которые должны учитываться алгоритмом управления. Такой метод
управления является эффективным при необходимости быстрого перевода рабочего органа из одного положения в
другое, не требующее высокой точности позиционирования. Кроме того, метод обладает достаточной сложностью реализации.
Метод последовательных корректировок положения наиболее широко применяется в цифровых системах управления.
В этом случае алгоритм управления по вектору скорости формируется как приращение координат манипулятора за один
цикл вычисления алгоритма.
Недостатком метода является частая выборка узловых точек сложной траектории, чтобы переходы от одной точки к
другой при планировании траектории движения не меняли принципиально необходимой картины движения.
Приближенные методы. При синтезе системы управления манипулятором пользуются приближенными решениями,
которые вытекают из ограниченности задания значений координат. Обычно берут по три значения: два крайних и одно
среднее, и для них вычисляют обратную матрицу Якоби, зависящей от конфигурации манипулятора, для всех других
значений координат (в том числе и узловых, характерных точек траектории) обратная матрица вычисляется интерполированием.
Во многих случаях, особенно при наличии обратной связи по положению, этого оказывается вполне достаточно при
достижении конечной цели управления.
Недостатком метода являются возникающие при интерполяции ошибки, достигающие большого значения, особенно при
отсутствии обратной связи по положению.
Метод управления по вектору силы. К недостаткам метода управления по вектору скорости следует отнести
невозможность обеспечивать формализацию стремления перемещения рабочих органов промышленных роботов в заданном
направлении, если на заданной траектории встречаются точки, в которых матрица конфигурации манипулятора является
вырожденной.
Тенденция к упрощению процесса управления и обусловленных этим вычислений привели к использованию метода управления
по вектору силы, в котором имитационно реализуется идея управления по заданному направлению. В действительности к
манипулятору не прилагаются никакие силы, но следящие приводы развивают такую совокупность обобщенных сил, которые
динамически эквивалентны заданным силам, имитирующим их приложение к манипулятору. Вычислитель, получив на входе
задающие сигналы, определяет обобщенные силы, отнесенные к координатам, непосредственно управляемым приводом. В
свою очередь, приводы постоянно вырабатывают такие обобщенные силы, которые получаются на выходе вычислителя. В
эти обобщенные силы могут автоматически вводиться поправки регуляторами и компенсаторами.
1.2. Анализ существующих методов компенсации нелинейностей и развязки взаимодействий в манипуляционных
промышленных роботах.
Основной задачей управления промышленными роботами является генерирование внешних моментов u(t) таким образом,
чтобы движение робота осуществлялось по выбранной траектории. Движение робота обычно осуществляется двумя
различными контролируемыми фазами. Первой из них является контоольная фаза грубого движения, во время которой
робот перемещается от изначальной позиции в окрестность места расположения заданной цели вдоль предварительно
определенной траектории. Второй контрольной фазой является стадия точного движения, когда рабочий орган робота
динамически взаимодейсгеует с объектом, используя при этом информационный канал обратной связи от внешних
датчиков для выполнения задачи.
В случае, если в роботах используется традиционная следящая техника, то нелинейности и взаимодействия,
присутствующие в динамике манипулятора, не могут быть скомпенсированы на стадии грубого движения. С повышением
требований к рабочим характеристикам промышленных роботов становится необходимым принятия во внимание
перечисленных динамических эффектов. Поэтому в течение последнего времени было предложено большое число
усовершенствований в схемах и алгоритмах непосредственного контроля промышленных роботов.
Некоторыми исследователями было предложено использовать линеаризованные модели систем в качестве основы для
дальнейшей реализации развязки регулирования. Кан и Рот разработали приближенную модель оптимального контроллера,
которая приводила к субоптимальному регулированию. Субоптимальное регулирование возникало в результате приближенной
замены нелинейной системы линейной и последующего аналитического нахождения оптимального управления для линейной
системы. Был также предложен метод линейного регулирования по многим переменным. Однако, основанная на линеаризованной
модели система регулирования может оказаться практически неприемлемой, если реальные рабочие условия начнут отличаться
от условий, заложенных при линеаризации. Это может привести к нежелаемым отклонениям реакции робота от заданной
траектории, как это было показано Фрюндом при моделировании различных методов регулирования.
Одним из первых методов, в которых робот рассматривается как нелинейная, взаимосвязанная система со многими входами
и многими выходами, была методика вычислений вращающих моментов, исследованная Полом, Маркевичем. Этот метод
основан на использовании отрицательной обратной и положительной обратной связей. Положительная обратная связь
используется для компенсации сил взаимодействия, возникающих между сочленениями, а с помощью отрицательной обратной
связи производится вычисление необходимых корректирующих вращательных моментов для компенсации любых отклонений
от заданной траектории. При этом полагается , что возможно точное вычисление инерционных сил реакции, силы Кориолиса
и центростремительной силы, а также гравитационных сил. Таким образом, эксплуатационные характеристики данной системы
регулирования в значительной степени зависят от точности используемой модели. Метод определения вращающих моментов
требует значительного количества вычислений, что часто рассматривается как его недостаток.
Регулирование скорости спроектированного движения представляет собой методику определения переменных скоростей движения
сочленения, необходимых для обеспечения перемещения концевой точки робота в заданном направлении. При такой схеме
управления все установленные траектории задаются в декартовых координатах. Это является определенным преимуществом,
поскольку большинство пользователей, вероятно, с большей легкостью могут задать последовательность перемещения в
декартовых координатах, чем в переменных координатах местоположения соединения. Способы вычисления вращающих моментов
и регулирования скорости спроектированного движения совмещены в методе регулирования ускорения спроектированного движения.
В ЭТОМ методе предполагается, что требуемые местоположения, скорости и ускорения заданного движения руки определяются
пользователем. Перечисленные методы также обладают недостатками: они требуют наличия детализованной динамической модели
и длительного машинного времени для осуществления вычислений.
Основное достоинство различных методов адаптивного регулирования является отсутствие необходимости использования
модели динамики робота. В эталонной модели адаптивного контроля выбирается соответствующая эталоном модель, а
алгоритм адаптации модифицирует коэффициенты усиления в каналах обратной связи контроллеров. Алгоритм адаптации
задается разницей между выходными сигналами эталонной модели и фактическими выходными периметрами робота. Управление
роботом осуществляется регулированием коэффициентов усиления в каналах обратной связи для местоположения и скорости,
так чтобы его характеристики замкнутого контура были близки к эталонной модели. Недостатком метода является кропотливость
и многомерность при реализации
Новое течение в проектировании управляющих систем для промышленных роботов является использование теории систем
с переменной структурой. В системах с переменной структурой на поверхности переключения имеет место так называемый
скользящий режим. При работе в скользящем режиме система остается нечувствительной к изменениям параметров и
возмущениям. Создание управления, индуцирующего скользящий режим, не требует точного моделирования; оказывается
достаточным только знать соотношения между параметрами модели. Однако, этот метод обладает одним недостатком,
вытекающим из минимизации времени решения: точное определение моментов включения регулирующих входных сигналов
оказывается затруднительным.
Вверх
2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОМЫШЛЕННОГО РОБОТА ТИПА PUMA-560
С МИНИМАЛЬНОЙ КОНФИГУРАЦИЕЙ
2.1. Математическая модель кинематики промышленного робота
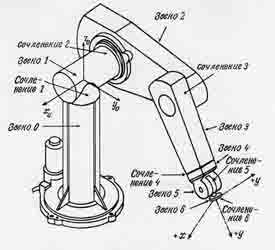 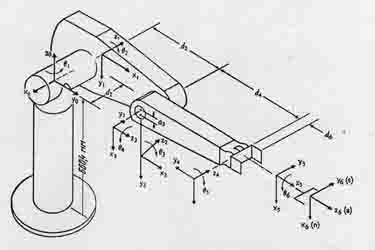
Рис. 2.1 - Манипулятор PUMA-560.
Понятие "робот с минимальной конфигурацией" означает, что будут рассматриваться три
первые звена робота, которые определяют положение схвата манипулятора в пространстве.
Иначе говоря, не будут рассматриваться последние три ступени подвижности, которые
определяют ориентацию схвата.
Для рассматриваемого робота согласно известны матрицы однородных преобразований
координат для перехода от i-ой к (i-1)-ой системе координат:
Для манипуляционного робота типа PUMA-560, все сочленения которого вращательные,
параметры di и 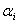 являются конструктивными
параметрами сочленений. Параметр qi является переменной величиной. Конкретные
значения конструктивных параметров, заимствованные из, приведены в таблицах 1 и 2. являются конструктивными
параметрами сочленений. Параметр qi является переменной величиной. Конкретные
значения конструктивных параметров, заимствованные из, приведены в таблицах 1 и 2.
Таблица 1
Конструктивные параметры робота PUMA-560
| a2,м |
a3,м |
a4,м |
a5,м |
| 0.432 |
0.019 |
0.125 |
0.432 |
Таблица 2
Массо-инерционные характеристики робота PUMA-560
| Звено |
Масса |
Центры масс |
Радиусы инерции |
| i |
mi,кг |
xi,м |
yi,м |
zi,м |
kxi,м |
kyi,м |
kzi,м |
| 1 |
33.5 |
0 |
0 |
0.08 |
0.0451 |
0.0451 |
0.00579 |
| 2 |
73.3 |
-0.216 |
0 |
0.2175 |
0.05657 |
0.1847 |
0.1408 |
| 3 |
36.3 |
0 |
0 |
0.216 |
0.06728 |
0.06791 |
0.0036 |
| 4 |
8.95 |
0 |
0.02 |
0 |
0.00316 |
0.00211 |
0.00316 |
Для получения однородной матрицы 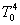 , определяющей положение
схвата манипулятора в пространстве, необходимо выполнить (в соответствии с формализмом
Денавита-Хартенберга) операции перемножения матриц , определяющей положение
схвата манипулятора в пространстве, необходимо выполнить (в соответствии с формализмом
Денавита-Хартенберга) операции перемножения матриц 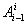 для i=1
для i=1 4: 4:
|
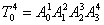
|
(2.5) |
В данной матрице нас интересует 4-й столбец, являющийся вектором положения схвата
рассматриваемого манипулятора, координаты которого имеют вид:
где
Полученный вектор 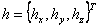 является нелинейным отображением выходных координат
системы, который в дальнейшем используется при линеаризации уравнений динамики манипулятора. является нелинейным отображением выходных координат
системы, который в дальнейшем используется при линеаризации уравнений динамики манипулятора.
2. Математическая модель динамики промышленного робота типа PUMA-560 в форме уравнения Лагранжа-Эйлера
Рассмотрим робот с п кинематическими парами, не имеющий избыточных степеней подвижности, у которого n - мерный
вектор моментов t(t) в кинематических парах связан с n - мерным вектором Q(t) углов поворота в шарнирах нелинейным
динамическим уравнением движения:
|
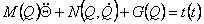
|
(2.9) |
где M(Q) - симметричная положительно определенная матрица инерции размерностью n х n,
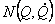 - n - мерный вектор-столбец моментов, обусловленных силами Кориолиса и центробежными силами: - n - мерный вектор-столбец моментов, обусловленных силами Кориолиса и центробежными силами:
|
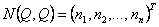
|
(2.10) |
|
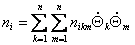
|
(2.11) |
G(Q) - n - мерный вектор гравитационной нагрузки;
Уравнение (2.9) описывает динамику манипулятора в форме Эйлера-Лагранжа. Для приведения нелинейных
дифференциальных уравнений (2.9) к специальному виду, введем обозначение:
|
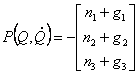
|
(2.12) |
Тогда уравнение (2.9) примет вид:
|
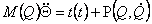
|
(2.13) |
Уравнение (2.13) в дальнейшем будет использовано при получении нелинейного уравнения специального вида.
Задача управления манипулятором заключается в создании такой системы управления, которая обеспечивает
отслеживание вектором углов поворота в шарнирах Q(t) любой заданной (опорной) траектории Qr(t),
где Qr(t) - n - мерный вектор-столбец произвольных функций времени. Целесообразно допустить, что
эти функции имеют производные первого и второго порядков, т.е. требуемые угловая скорость
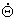 r(t) и угловое ускорение r(t) и угловое ускорение 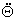 r(t)
существуют и доступны непосредственно, без необходимости операции дифференцирования Qr(t). Желательно также,
чтобы система управления манипулятором обеспечивала отслеживание траектории независимо от массы груза m, т.е.
чтобы динамические характеристики манипулятора были нечувствительны к величине полезной нагрузки. r(t)
существуют и доступны непосредственно, без необходимости операции дифференцирования Qr(t). Желательно также,
чтобы система управления манипулятором обеспечивала отслеживание траектории независимо от массы груза m, т.е.
чтобы динамические характеристики манипулятора были нечувствительны к величине полезной нагрузки.
Вверх
3. ЛИНЕАРИЗАЦИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДИНАМИКИ ПРОМЫШЛЕННОГО РОБОТА ТИПА PUMA-560
3.1 Линеаризация математической модели динамики робота на основе разложения вряд Тейлора
Аппроксимируем нелинейную математическую модель динамической системы (2.8) на временном интервале
ti<t<ti+Dt путем разложения в ряд Тейлора в окрестности номинальной операционной (рабочей) точки
линейной инвариантной по времени многомерной моделью
|
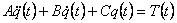
|
(3.1) |
где q(t) и T(t) - отклонения векторов углов поворота и моментов в шарнирах от своих номинальных значений
t(ti) и Q(ti) в рабочей точке P={t(ti),Q(ti),Q(ti)}, т.е
|
q(t)=Q(t)-Q(ti)
|
(3.2) |
|
T(t)=t(t)-t(ti)
|
(3.3) |
Три матрицы А, В, С размерностью n х n, входящие в линеаризованную модель (3.1), зависят от положения
рабочей точки Р и могут быть, получены из выражений:
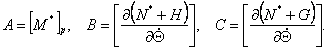
и матрица А всегда симметрическая, положительно определенная и, следовательно, не вырожденная.
Уравнение (3.1) представляет собой систему связанных линейных, не зависящих от времени дифференциальных
уравнений, описывающих динамику робота в приращениях при наличии возмущений в окрестности номинальной
операционной точки Р.
Возможны два варианта представления линеаризованной модели робота (3.1), а именно: модель в пространстве состояния,
т.е. во временной области, и модель в области комплексной переменной, т.е. в частотной области.
Для составления модели робота в пространстве состояний определяют элементы выражений 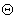 и
и 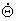 как переменные состояния системы, и уравнение (3.1) переписывают в стандартном формате : как переменные состояния системы, и уравнение (3.1) переписывают в стандартном формате :
|
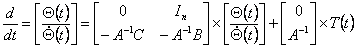
|
(3.5) |
Порядок этой модели равен 2n, вектор состояния 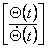 имеет размерность
2n имеет размерность
2n 1, все векторы рассматриваются во временной области. 1, все векторы рассматриваются во временной области.
Модель робота в частотной области составляем с помощью преобразования Лапласа из уравнений (3.1),
в результате чего получаем:
|
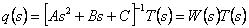
|
(3.6) |
где T(s) и q(s) - n - мерные векторы входа и выхода системы в частотной области.
3.2 Приведение уравнений динамики промышленного робота типа PUMA-560 в форме
Лагранжа-Эйлера к специальному виду
Для получения нелинейного дифференциального уравнения специального вида введем следующие
обозначения для обобщенных координат:
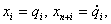
вектор (x1,x2,…,x2n) обозначается X, вектор (x1,x2,…,xn)
обозначается 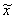 . Уравнение (2.9) можно представить в стандартной форме специального
вида, если учесть ранее введенные обозначения: . Уравнение (2.9) можно представить в стандартной форме специального
вида, если учесть ранее введенные обозначения:
|
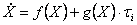
|
(3.7) |
Содержание нелинейных функций f(x) и g(x) в уравнении (3.7) станет понятным при его записи в форме компонентов:
|

|
(3.8) |
Таким образом получено векторно-матричное уравнение (3.8), на основе которого будет осуществлена линеаризация
динамической модели манипулятора с применением диффеоморфного преобразования координат и нелинейной обратной
связи по состоянию.
3.3 Линеаризация математической модели динамики робота на основе диффеоморфного преобразования координат и
нелинейной обратной связи по состоянию
Для линеаризации динамической модели промышленного робота типа PUMA-560 вводится нелинейная обратная связь вида:
и диффеоморфное преобразование Т(х) такое, что после осуществления нелинейной обратной связи и диффеоморфного
преобразования координат новая (преобразованная) система является линейной в Бруновской канонической форме с
развязанным выходом.
В выражении (3.9) фигурируют следующие обозначения:
U(x) - вектор управляющих воздействий, приложенных к манипулятору робота;
а(х) - векторная функция;
b(х) - неособая матрица;
V- вектор входных воздействий системы;
Нелинейная обратная связь может быть представлена в следующем виде:
|
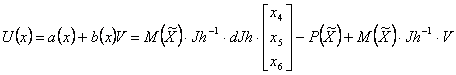
|
(3.10) |
где
|
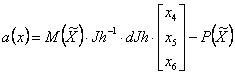
|
(3.11) |
|
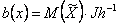
|
(3.12) |
Jh - матрица Якоби функции;
Jh-1 - матрица, обратная матрице Якоби;
DJh - матрица, определяемая согласно выражениям:
|

|
(3.13) |
|

|
(3.14) |
Диффеоморфное преобразование координат имеет следующий вид:
|

|
(3.15) |
где Lf- производные Ли;
|
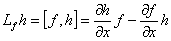
|
(3.16) |
Частные производные 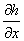 и и 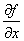 являются матрицами Якоби;
являются матрицами Якоби;
С использованием приведенной выше нелинейной обратной связи по состоянию и диффеоморфного преобразования
динамическая модель манипулятора представляется в канонической форме Brunovsky с декомпозицией по выходным
переменным:
|
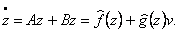
|
(3.17) |
|
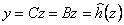
|
(3.18) |
где z - вектор состояния в преобразованной системе координат размерности (6x1);
А - блочно-диагональная матрица размерности (6x6), характеризующая
декомпозицию состояний звеньев преобразованной модели робота;
В - блочно - диагональная матрица размерности (6x3), отражающая декомпозицию
управляющих воздействий на звенья преобразованной модели робота;
С - блочно - диагональная матрица размерности (3x6), определяющая декомпозицию
выходных координат шарниров преобразованной модели робота;
|
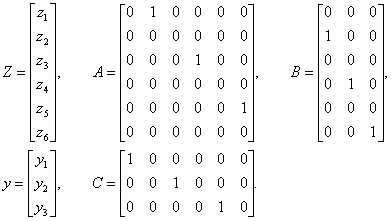
|
(3.19) |
Динамическая система, описанная уравнениями (3.17) и (3.18), состоит из трех независимых
подсистем следующей формы:
|
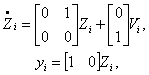
|
(3.20) |
где
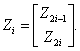
Данная линейная система с развязанным выходом показана схематически как блок BCLS
(Бруновская каноническая линейная система) на рис.3.1.
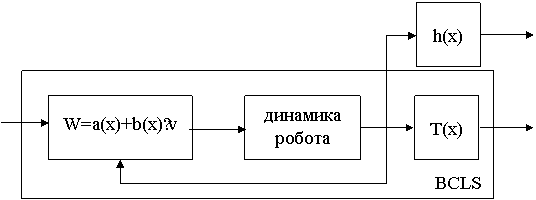
Рис.3.1 - Бруновская каноническая линейная система
Линеаризация, осуществляемая нелинейной обратной связью, является "внешней линеаризацией" в отличие
от обычной "внутренней линеаризации" (разложение в ряд Тейлора). Нелинейный характер исходной системы
не меняется. Линеаризацию системы нелинейной обратной связью можно назвать "точной линеаризацией" в
смысле управления. Точная общая линеаризация системы и развязка выхода, осуществленные нелинейной
обратной связью по состоянию и диффеоморфным преобразованием координат, создают линейную систему.
Полученная система является неустойчивой, так как каждая линейная подсистема имеет кратные нулевые
полюса. Следовательно, необходимо провести стабилизацию полученной линейной системы.
В результате проведенной линеаризации динамической модели робота с помощью нелинейной обратной связи
по состоянию и диффеоморфного преобразования координат, получена линеаризованная математическая модель
с декомпозицией состояния по сочленениям и с развязанным выходом манипулятора. На основе полученной
математической модели можно синтезировать алгоритмы оптимального управления манипулятором робота хорошо
разработанными линейными методами.
Вверх
4. СИНТЕЗ АЛГОРИТМОВ УПРАВЛЕНИЯ ПРОМЫШЛЕННЫМ РОБОТОМ ТИПА PUMA-560 МИНИМАЛЬНОЙ КОНФИГУРАЦИИ
4.1. Синтез алгоритмов многомерной системы управления промышленным роботом - многомерного
регулятора с комбинированным управлением
Подход к синтезу системы управления движением в кинематических парах, используемый в настоящей работе,
основан на концепции так называемых "обратных систем". Рассмотрим линейную, не зависящую от времени,
многомерную установку (объект регулирования)
где u и у - m-мерные векторы - столбцы входа и выхода, a W(s) - ее передаточная функция в виде матрицы
размерностью тхт. Обратным отображением (инверсией) этой установки является динамическая система, у
которой передаточная функция
Когда при последовательном соединении объекту управления (4.1) предшествует его инверсия (4.2), на вход
которой подается требуемый выходной сигнал yd (t) объекта, инверсный регулятор будет генерировать
соответствующее управляющее воздействие, обеспечивая на выходе установки воспроизведение сигнала у (t),
так как по определению произведение передаточной функции объекта и ее инверсии есть единичная матрица
размерности mхm
Данная концепция может быть использована для управления нелинейными объектами, в частности, применительно к роботам.
В случае небольших отклонений параметров объекта в окрестности рабочей точки Р нелинейная установка апроксимируется
квазилинейной инвариантной по времени моделью W1(s) на малом временном интервале
ti<t<ti+ t. В этом интервале времени инверсия
Qi(s) установки используется в качестве регулятора прямого канала управления для генерирования управляющего
воздействия uпк(t). Затем коэффициенты усиления регулятора прямого канала управления "обновляются"
(настраиваются) таким образом, чтобы компенсировать изменения во времени коэффициентов линеаризованной модели
Wi(s), обусловленные изменениями положения рабочей точки Р. Когда регулятор прямого канала управления
является точной инверсией объекта управления, ошибка отслеживания e(t)=yd(t)-y(t), представляющая
собой разность между входом регулятора (у) и выходом системы (yd) будет равна нулю. Следовательно,
представляется логичным рассматривать ошибку отслеживания е(t) как меру отклонения регулятора прямого канала
управления от точной инверсии объекта. Эта информация используется для настройки параметров регулятора прямого канала
управления, причем настройка ведется таким образом, чтобы поведение регулятора было точной инверсией поведения объекта
управления, что обеспечивает качественное отслеживание заданной траектории yd(t). t. В этом интервале времени инверсия
Qi(s) установки используется в качестве регулятора прямого канала управления для генерирования управляющего
воздействия uпк(t). Затем коэффициенты усиления регулятора прямого канала управления "обновляются"
(настраиваются) таким образом, чтобы компенсировать изменения во времени коэффициентов линеаризованной модели
Wi(s), обусловленные изменениями положения рабочей точки Р. Когда регулятор прямого канала управления
является точной инверсией объекта управления, ошибка отслеживания e(t)=yd(t)-y(t), представляющая
собой разность между входом регулятора (у) и выходом системы (yd) будет равна нулю. Следовательно,
представляется логичным рассматривать ошибку отслеживания е(t) как меру отклонения регулятора прямого канала
управления от точной инверсии объекта. Эта информация используется для настройки параметров регулятора прямого канала
управления, причем настройка ведется таким образом, чтобы поведение регулятора было точной инверсией поведения объекта
управления, что обеспечивает качественное отслеживание заданной траектории yd(t).
Кроме того, для повышения устойчивости замкнутой системы управления и улучшения качества переходных
процессов используется регулятор цепи обратной связи Ki(s), генерирующий для объекта управления
управляющий сигнал Uoc(t) в рабочей точке Р. Коэффициенты цепи обратной связи также постоянно
настраиваются в соответствии с ошибкой е(t) для компенсации изменений Wi(s). Кроме
того, при реализации закона управления синтезируется и используется дополнительный сигнал uрт(t),
соответствующий рабочей точке Р. Этот сигнал помогает улучшить качество управления, обеспечивая более быструю
адаптацию к изменениям параметров установки, и увеличивает гибкость системы управления. Исходя из всего
вышесказанного, общий закон управления определяется выражением:
|
u(t)=uпк(t)+uос(t)+uрт(t)
|
(4.4) |
Описанная методика синтеза проиллюстрирована блок-схемой на рис. 4.1
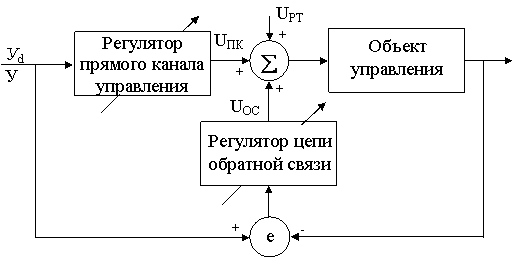
Рис. 4.1. - Структура системы управления
4.1.1. Синтез регулятора прямого канала управления
Линеаризованную модель (5.4.3.1) динамики манипулятора можно представить моделью в частотной области
(через передаточную функцию)
|
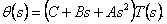
|
(4.5) |
Учитывая вышеизложенное, в качестве передаточной функции Q(s) размерностью n х n регулятора прямого
канала управления выбирается инверсия линеаризованной модели (4.5), т. е.
|
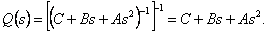
|
(4.6) |
Уравнение (4.6) дает простое выражение инверсии линеаризованной модели (3.1) манипулятора, что обеспечивает
возможность практической реализации Q(s). Необходимо отметить, что инверсия Q(s) многомерного
объекта регулирования W(s) в общем случае представляет собой сложную динамическую систему. Тогда закон
управления, реализуемый регулятором прямого канала управления, задается выражением:
|
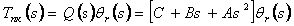
|
(4.7) |
или
|
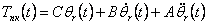
|
(4.8) |
где 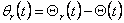 - требуемый n-мерный вектор-столбец приращений углов поворота
в шарнирах. Реализация закона управления (4.8) с использованием регулятора прямого канала управления,
представляющего собой инверсию робота, осуществляется непосредственной подачей в прямой канал управления
требуемых сигналов положения - требуемый n-мерный вектор-столбец приращений углов поворота
в шарнирах. Реализация закона управления (4.8) с использованием регулятора прямого канала управления,
представляющего собой инверсию робота, осуществляется непосредственной подачей в прямой канал управления
требуемых сигналов положения 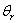 , скорости , скорости 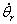 и ускорения
и ускорения 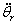 и умножения их на матрицы С, В и А соответственно. и умножения их на матрицы С, В и А соответственно.
4.1.2. Синтез регулятора обратной связи
Для повышения устойчивости замкнутой системы управления манипулятором и улучшения качества переходных процессов
используется регулятор цепи обратной связи K(s):
где Kp и Kv - матрицы (размерностью п х п) коэффициентов обратной связи по положению и скорости,
которые необходимо определить. Закон управления, реализуемый регулятором цепи обратной связи, имеет вид:
|
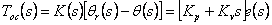
|
(4.10) |
или
|
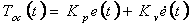
|
(4.11) |
где 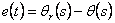 - n-мерный вектор приращений ошибки отслеживания по положению.
Фактически уравнение (4.11) представляет собой закон управления канала обратной связи по состоянию для
линеаризованной модели (3.1) робота, поскольку оно содержит сигналы обратной связи как по - n-мерный вектор приращений ошибки отслеживания по положению.
Фактически уравнение (4.11) представляет собой закон управления канала обратной связи по состоянию для
линеаризованной модели (3.1) робота, поскольку оно содержит сигналы обратной связи как по
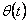 , так и по , так и по 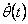 . Учитывая
результаты вышеприведенного анализа, построим систему управления движением в кинематических парах
"в приращениях", скомбинировав регулятор цепи обратной связи K(s) и регулятор прямого канала управления
Q(s) как показано на блок - схеме рис. 4.2. . Учитывая
результаты вышеприведенного анализа, построим систему управления движением в кинематических парах
"в приращениях", скомбинировав регулятор цепи обратной связи K(s) и регулятор прямого канала управления
Q(s) как показано на блок - схеме рис. 4.2.
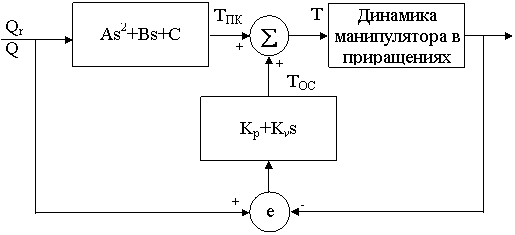
Рис. 4.2. - Система управления движением манипулятора в приращениях
С учетом рис. 4.2 закон движения в приращениях в частотной области задается следующим образом :
|
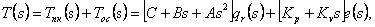
|
(4.12) |
или во временной области
|
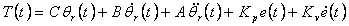
|
(4.13) |
Когда закон управления движением в приращениях применяется к нелинейной модели манипулятора,
"полный" закон управления задается выражением:
|
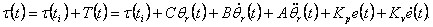
|
(4.14) |
Видно, что "полный" закон управления представляет собой сумму двух компонент. Первой из них
является значение вектора моментов в кинематических парах, приложенного в номинальной рабочей точке Р, т. е.
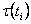 . Вторая компонента обусловлена регуляторами K(s) и . Вторая компонента обусловлена регуляторами K(s) и
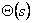 , обеспечивающими управление движением в приращениях. Пусть далее n
- мерный "полный" заданный вектор описывается выражением , обеспечивающими управление движением в приращениях. Пусть далее n
- мерный "полный" заданный вектор описывается выражением 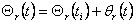 ,
a n-мерный "полный" вектор углов поворота в шарнирах равен ,
a n-мерный "полный" вектор углов поворота в шарнирах равен 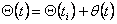 .
Подстановка этих выражений в уравнение (4.14) дает "полный" закон управления, определенный через
"суммарные" переменные: .
Подстановка этих выражений в уравнение (4.14) дает "полный" закон управления, определенный через
"суммарные" переменные:
|
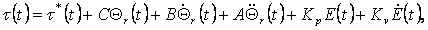
|
(4.15) |
где 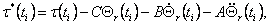 - n-мерный "суммарный" вектор ошибки отслеживания. Видно, что кроме
двух членов, соответствующих регуляторам цепи обратной связи и прямого канала управления, в полном законе управления
(4.15) присутствует третий член - n-мерный "суммарный" вектор ошибки отслеживания. Видно, что кроме
двух членов, соответствующих регуляторам цепи обратной связи и прямого канала управления, в полном законе управления
(4.15) присутствует третий член
|
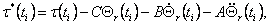
|
(4.16) |
отражающий влияние положения рабочей точки Р.
4.2. Синтез алгоритмов управления промышленным роботом на основе диффеоморфного преобразования координат и нелинейной
обратной связи по состоянию - диффеометрического регулятора
Вначале стабилизируется новая линейная и разомкнутая по выходу динамическая система. Затем для обеспечения
устойчивости стабилизированной системы к неопределенностям в значениях параметров робота и задания,
добавляется контур оптимальной коррекции ошибок для каждой линейной подсистемы с разомкнутым выходом.
4.2.1. Стабилизация
Стабилизация осуществляется использованием контура линейной обратной связи F в системе и желаемым установлением
полюсов замкнутой системы. Поскольку F является постоянной блочно - диагональной матрицей, вся система останется
линейной с разомкнутым выходом, называемой L&D - блоком (рис. 4.3). Для нового контура обратной связи вводятся
линейные ПД - регуляторы:
|
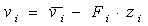
|
(4.17) |
где Fi=[fi1 fi2]. Тогда система (3.20) принимает вид :
|
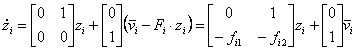 , ,
|
(4.18) |
Полюсы каждой подсистемы определяются выражением:
|
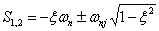 , ,
|
(4.19) |
где 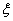 - коэффициент затухания; - коэффициент затухания; 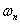 - собственная частота;
- собственная частота; 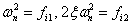 . .
Желаемый входной сигнал для каждой подсистемы можно получить из уравнений:
|
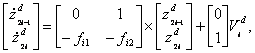 , ,
|
(4.20) |
|
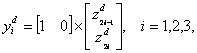 , ,
|
(4.21) |
где 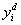 - желаемая траектория. - желаемая траектория.
4.2.2 Оптимизация ошибок
Для синтеза оптимальной системы управления необходимо рассмотреть ошибки
|
 , ,
|
(4.22) |
Из уравнений (4.18) - (4.22) можно получить
|
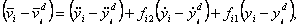 , ,
|
(4.23) |
т.е.
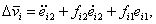
или
|
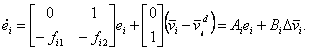 , ,
|
(4.24) |
В систему управления вводится контур оптимальной коррекции ошибок, обеспечивающий минимизацию целевой функции
|
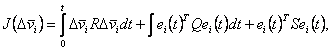 , ,
|
(4.25) |
где R - положительно-определенная матрица; Q и S - положительно-полуопределенные матрицы;
Т - время окончания процесса. В соответствии с линейной теорией оптимального управления оптимальная
коррекция определяется выражением:
|
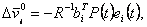 , ,
|
(4.26) |
где
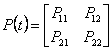
является положительно-определенной матрицей решения уравнения Риккати
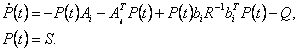
Если рассматривать установившееся решение при 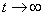 то то
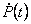 =0 и уравнение Риккати принимает форму алгебраического уравнения: =0 и уравнение Риккати принимает форму алгебраического уравнения:
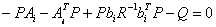
Отсюда (4.27) принимает вид:
|
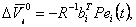 , ,
|
(4.27) |
или
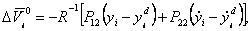
где
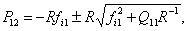
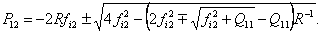
Структурная схема системы управления с оптимальной коррекцией ошибок представлена на рис. 4.3.
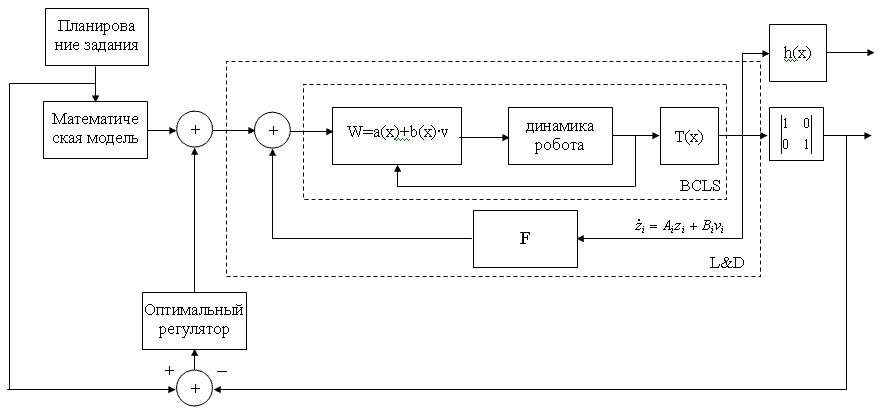
Рис. 4.3. - Система управления манипуляционным роботом с диффеометрическим регулятором
Вверх
5. ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА РАБОТОСПОСОБНОСТИ
СИНТЕЗИРОВАННЫХ АЛГОРИТМОВ УПРАВЛЕНИЯ НА ПЭВМ
С целью экспериментальной проверки работоспособности синтезированных алгоритмов управления было проведено
моделирование на ПЭВМ IBM PC. Для этого разработана программа в среде MATLAB. Проведение линеаризации прогрессивным
методом, основанным на применении теории групп Ли вручную практически невозможно. Объектом моделирования являются
регулятор, построенный с использованием классической теории многомерных систем (многомерный регулятор) и регулятор,
синтезированный на основе указанного новейшего метода управления. Моделирование проведено в двух режимах:
при отсутствии (1 режим) и при наличии (2 режим) параметрических возмущений.

Рис 5.1. - Пример работы манипулятора
Сравнительная оценка экспериментальных результатов моделирования уравнений динамики робота минимальной конфигурации
с синтезированными многомерным и диффеометрическим регуляторами показывает существенное преимущество алгоритмов
управления, основанных на новейшем методе. Так, при значительном изменении массы нагрузки для новейшего метода
ошибка отслеживания траектории не превысила 0.1 мм, в то время как ошибка многомерного регулятора превысила 4 мм.
При наличии в системе модельных ошибок (отклонение параметров модели объекта на 50%) многомерный регулятор теряет
устойчивость, диффеометрический регулятор при моделировании в аналогичных условиях сохраняет устойчивость и
требуемую точность позиционирования (0.1 мм).
Вверх
6.РАЗРАБОТКА АЛГОРИТМОВ УПРАВЛЕНИЯ НА ОСНОВЕ РОБАСТНЫХ СИСТЕМ
Следующим этапом разработки системы является создание системы робастного управления, клторая базируется на
современных формализованных подходах к математическому моделированию, исследованию и проектированных систем.
При рассмотрении адаптивных систем управления мы стремились к наилучшему управлению с точки зрения заданного критерия
оптимальности. Адаптивная САУ, реагирует в процессе функционирования на изменение свойств ОУ и внешних воздействий и
приспосабливающееся к новым условиям на основе изменения структуры и параметров управления устройств с тем, чтобы
показатель качества достигал экстремального значения.
Главной задачей синтеза робастных систем управления является поиск закона управления который сохранял бы выходные
переменные системы и сигналы ошибки в заданных допустимых пределах несмотря на наличие неопределённостей в контуре
управления. Неопределённости могут принимать любые формы, однако наиболее существенными являются шумы, нелинейности,
и неточности в знании передаточной функции объекта управления. Поэтому дальнейшая разроботка будет посвешена разработке
робастного регулятора обеспечивающего работу системы в условиях заданной неопределённости.
Вверх
Список литературы
- Шахнипур М. Курс робототехники: Пер. с англ.- М.: Мир, 1990. - 527с.
- Фу К., Гонсалес Р., Ли К. Робототехника: Пер. с англ. М.: Мир, 1989. - 621с.
- Броккет Р. У. Алгебры Ли и группы в теории управления. Математические методы в теории систем. М.: Мир, 1979.
- Андреев Ю. Н. Дифференциально-геометрические методы в теории управления. Автоматика и телемехника 1982г. вып. 10.
- Системы очувствления и адаптивные промышленные роботы / В.Б. Брагин, Ю.Г. Войлов, Ю.Д. Жабитинский и др.;
Под общ. ред. Е.П. Попова, В.В. Клюева. - М.: Машиностроение, 1988. - 392с.
- Изерман Р. Цифровые системы упрвления: Пер. с англ. - М:Мир, 1984. - 541с.
- Уткин В.И Скользящие режимы в задачах оптимизации и управления. М.: Наука, 1981г. -368с.
- Y. L. Chen, Nonlinear feedback and computer control of robot arm, Ph. D. dissertation, Dept of System Science and Math.,
Washington Univ., St Louis, MO, Dec., 1984.
- Дьяконов В. Simulink 4. Специальный справочник.-СПб:Питер, 2002. - 528с.:ил.
- Дьяконов В. Круглов В. Математические пакеты расширения MATLAB. Специальный справочник.-СПб:Питер, 2001. - 480с.:ил.
|
















