
Биография
| Реферат
| Библиотека
| Отчет о поиске
| Ссылки
| Задание
Анимица А.В., СУА-06м
Руководитель доц. Рафиков Г.Ш.
Наукові праці Донецького державного технічного університету. Серія: Обчислювальна техніка та автоматизація, випуск 118: - Донецьк: ДонДТУ, ТОВ "Лебідь", 2007.-294с.,142-145.
Особенностью современного развития производства является широкое применение средств роботизации. Поэтому в последние годы быстро расширяется использование роботов, особенно в промышленной сфере, где первостепенным является требование большой производительности и более строгого контроля качества в связи с интенсивной международной конкуренцией. Следствием такого бурного развития стали весьма активные исследования в этой области, и на их основе были выработаны несколько подходов к созданию систем управления.
В настоящее время быстро развивается автоматизация дуговой сварки (сварка плавлением) с применением промышленных роботов, которая может применяться во всех отраслях при изготовлении металлоконструкций. Сваркой плавлением можно соединять практически все используемые для изготовления конструкций металлы и сплавы любой толщины. Этот процесс очень вреден для человека, связан с сильным шумом, воздействием дыма и интенсивного света (искрение), а автоматизация обеспечивает высокое качество швов, большую стабильность и скорость работы.
Основной проблемой управления дуговой сваркой является проблема точного позиционирования, т.е. точного отслеживания заданной траектории в пространстве и времени, при непрерывном контурном управлении для выполнения относительно сложных манипуляционных задач. Основными факторами, порождающими эту проблему, является существенная нелинейность динамической и кинематической модели, динамическая взаимосвязь между отдельными системами, а также незапланированные факторы: изменение программы траектории или неожиданное изменение полезной нагрузки.
Для устранения этих проблем применён новый общий метод компенсации взаимосвязей и нелинейностей дифференциальных уравнений динамики. Данный подход основан на идее получения «внешней линеаризации» сложной нелинейной системы с использованием диффеоморфного преобразования координат и нелинейной обратной связи по состоянию. Этот метод позволяет обеспечить поблочную развязку выхода; конструктивный алгоритм нахождения нелинейной обратной связи для подсистем, в которых число выходов может быть меньше или равно числу входов; развязку выходов нелинейной обратной связью с точки зрения состояния системы; для обеспечения устойчивости системы управления нелинейная обратная связь соединяется с контролером оптимальной коррекции ошибок.
Для применения этого метода уравнение динамики промышленного робота типа PUMA-560 преобразовано к специальному виду:
|
|
(1) |
Затем произведено диффеоморфное преобразование координат уравнения (1) с использованием производных Ли, определяемое согласно выражению:
|
|
(2) |
где Lf - производные Ли (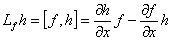 ).
).
В результате получена динамическая модель в канонической форме Brunovsky с декомпозицией по выходным переменным:
|
|
(3) |
где
|
|
(4) |
Динамическая система (3) состоит из трех независимых подсистем следующей формы:
|
|
(5) |
Данная система с развязанным выходом показана на рис. 1 как блок BCLS (Броуновская каноническая линейная система).

Рисунок 1 – Система управления с диффеоморфным регулятором
Решена задача синтеза алгоритмов стабилизации и оптимальной коррекции для обеспечения достаточно точного отслеживания заданной траектории движения сварочной головкой в пространстве и во времени.
Стабилизация осуществляется с использованием контура линейной обратной связи F в системе и желаемым установлением полюсов замкнутой системы. Выражение входного воздействия со стабилизацией имеет вид:
|
|
(6) |
Затем для обеспечения устойчивости стабилизированной системы к неопределённостям в значениях параметров робота и задания, добавлен контур оптимальной коррекции ошибок для каждой линейной подсистемы с разомкнутым выходом, letter-spacing:-.25pt'>обеспечивающий минимизацию целевой функции вида:
|
|
(7) |
Оптимальная коррекция определяется следующим выражением:
|
|
(8) |
где P(t) - положительно-определённая матрица решения уравнения Риккати:
|
|
(9) |
Произведена экспериментальная проверка работоспособности синтезированного алгоритма по выше изложенному методу в двух режимах при отсутствии и наличии параметрических возмущений.
Моделирование диффеометрического регулятора при отсутствии и при наличии возмущений показало, что ошибка отслеживания траектории не превышает 0.1мм. При значительном увеличении массы нагрузки и изменении параметров модели манипулятора ошибка отслеживания траектории (ошибка позиционирования) не превысила предельно допустимого значения 0.1мм. При отклонении параметров модели объекта на 50% диффеометрический регулятор сохранил устойчивость и требуемую точность позиционирования.
Перечень ссылок
Биография
| Реферат
| Библиотека
| Отчет о поиске
| Ссылки
| Задание