Анимица А.В., Рафиков Г.Ш. Разработка алгоритма управления роботом для сварочных работ

УДК 621.865.8

Анимица А.В., Рафиков Г.Ш. Украина(Донецк)

Тезисы доклада всеукраинской конференции "Автомптика 2007", г. Севастополь, 7-10 сентября 2007г., 112с.,34-35.

Разработка алгоритма управления манипуляционным промышленным роботом для выполнения сварочных работ с использованием диффеометрического регулятора и нелинейной ОС

В настоящее время сварка широко применяется во всех отраслях для изготовления новых и ремонта эксплуатируемых механизмов, конструкций и оборудования. Преимущества сварных конструкций общепризнанны, их повсеместно применяют взамен литых, клепаных и кованых. Эти преиму щества дают возможность уменьшить расход металла, снизить затраты труда, упростить конструкцию оборудования и сократить сроки изготовления. Одной из бурно развивающихся видов сварки является дуговая (сварка плавлением) которая может применяться во всех отраслях при изготовлении металлоконструкций. Преимущество этого вида сваркой в том, что можно соединять практически все используемые для изготовления конструкций металлы и сплавы любой толщины.

Одной из наиболее актуальных, в наше время, является задача разработки, создания и внедрения систем комплексной автоматизации процессов сварочного производства. Заметное место в решении этой задачи отводится промышленным роботам. Следствием этого стали весьма активные исследования в области создания систем управления промышленными роботами, и на их основе были выработаны несколько основных подходов.

Основной проблемой управления дуговой сваркой является проблема точного позиционирования, т.е. точного отслеживания заданной траектории в пространстве и времени, при непрерывном контурном управлении для выполнения относительно сложных манипуляционных задач. Основными факторами, порождающими эту проблему, является существенная нелинейность динамической и кинематической модели, динамическая взаимосвязь между отдельными системами, а также незапланированные факторы: изменение программы траектории или неожиданное изменение полезной нагрузки.

Для устранения проблем связанных с нелинейностью дифференциальных уравнений необходимо применить линеаризацию. Линеаризация, с помощью классического метода, с использованием разложения нелинейных дифференциальных уравнений в ряд Тейлора в окрестностях рабочей точки, нуждается в перенастройке параметров управления при изменении рабочей точки, поэтому данный метод очень громоздкий и требует быстродействующего аппаратного обеспечения.

Для устранения этих же проблем применён новый общий метод компенсации взаимосвязей и нелинейностей дифференциальных уравнений динамики с использованием диффеометрического регулятора и теории алгебры Ли. Данный подход основан на идее получения «внешней линеаризации» сложной нелинейной системы с использованием диффеоморфного преобразования координат и нелинейной обратной связи по состоянию. Этот метод позволяет обеспечить поблочную развязку выхода; конструктивный алгоритм нахождения нелинейной обратной связи для подсистем, в которых число выходов может быть меньше или равно числу входов; развязку выходов нелинейной обратной связью с точки зрения состояния системы; для обеспечения устойчивости системы управления нелинейная обратная связь соединяется с контроллером оптимальной коррекции ошибок.

Особенностью данного метода динамического управления является то, что нелинейное усилие в контроллере не нуждается в перенастройке коэффициентов усиления от задания к заданию. В данном случае такой контроллер является «интеллектуальным», так как он прямо реагирует на изменение условий задания.

Для использования данного метода был выполнен ряд преобразований над уравнениями динамики системы промышленного робота типа PUMA-560. Далее для линеаризации системы уравнений введена нелинейная обратная связь и произведено диффеоморфное преобразование координат уравнения с использованием производных Ли. В результате линеаризации получена динамическая модель в канонической форме Brunovsky с декомпозицией по выходным переменным. Данную модель можно разбить на шесть независимых подсистем, что позволяет рассматривать их как отдельные системы и выводы об устойчивости можно делать по каждой системе в отдельности.

Полученная система после линеаризации является неустойчивой, так как каждая линейная подсистема имеет полюса, равные нулю. Иначе говоря система имеет кратный нулевой полюс. Поскольку полученная динамическая модель линейна, поэтому можно синтезировать алгоритм оптимального управления хорошо разработанными линейными методами.

Вначале была стабилизирована новая линейная и разомкнутая по выходу система. Затем для обеспечения устойчивости стабилизированной системы к неопределённостям в значениях параметров робота был добавлен контур оптимальной коррекции ошибок для каждой линейной подсистемы с разомкнутым выходом.

Стабилизация осуществляется с использованием контура линейной обратной связи F(f_i1,f_i2) в системе и желаемым установлением полюсов замкнутой системы.

Затем для обеспечения устойчивости стабилизированной системы к неопределённостям в значениях параметров робота и задания, добавлен контур оптимальной коррекции ошибок для каждой линейной подсистемы с разомкнутым выходом, где уравнение ошибки будет иметь вид:

(1)

которая обеспечивает минимизацию целевой функции вида:

(2)

где R – положительно определённая матрица;
Q и S – положительно полуопределённая матрица;
T – конечное время.

В соответствии с теорией оптимального управления оптимальная коррекция определяется следующим выражением:

(3)

где P(t) - положительно-определённая матрица решения уравнения Риккати:

(4)

Если рассматривать установившееся решение при , то 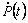=0 и уравнение Риккати принимает форму алгебраического уравнения:

(5)

Решив уравнение Риккати (5) и подставив P в выражение (3) получим окончательный вектор оптимальной коррекции:

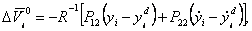
где

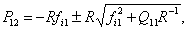
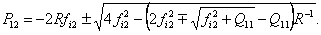
Для проверки работоспособности алгоритма было произведено моделирование по выше изложенному методу в двух режимах при отсутствии и наличии параметрических возмущений.

Результаты моделирования системы с диффеометрическим регулятором при отсутствии и при наличии возмущений показало, что ошибка отслеживания траектории не превышает 0.1мм. При значительном увеличении массы нагрузки и изменении параметров модели манипулятора ошибка отслеживания траектории (ошибка позиционирования) не превысила предельно допустимого значения 0.1мм. При отклонении параметров модели объекта на 50% диффеометрический регулятор сохранил устойчивость и требуемую точность позиционирования.

Анимица Андрей Вячеславович, ст. гр. СУА-06м, ФКИТА, ДонНТУ
Рафиков Гыяз Шагиевич, к.т.н.,доц. кафедры АТ, ДонНТУ