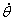 в завихрение t сварочного
инструмента следующим образом:
в завихрение t сварочного
инструмента следующим образом:
Биография
| Реферат
| Библиотека
| Отчет о поиске
| Ссылки
| Задание
Перевод с английского Анимица А.В.
Источник: http://www.professeurs.polymtl.ca/luc.baron/doc/c14.pdf
Люк Барон
Департамент инженерных машин
Политехнический институт, C.P. 6079, succ. CV
Монреаль, Квебек, Канадский H3C 3A7
E-mail: baron@meca.polymtl.ca
Резюме: Ввиду симметрии электрода сварки вокруг ее оси, операция сварки может быть выполнена только с пятью степенями свободы (СС). Однако, когда выполненный робот имеет шесть СС, стратегия предотвращения пределов перемещения может быть выполнена используя увеличенную матрицу Якобиант, так же как увеличенный вектор объединенных скоростей, действительным вращением вокруг оси электрода. В этой статье, мы изучаем адекватность этого подхода.
Резюме: из-за симметрии сварочного инструмента вокруг оси электрода, операция дуговой сварки может быть выполнена только с пятью степенями свободы (СС). Однако, когда выполнено роботом с шестью СС, стратегия предотвращения пределов перемещения в сочленгениях может быть осуществлена на увеличенной якобиевской матрице, и ее передача увеличивала вектор объединенной нормы, действительным вращением вокруг оси электрода. Этот подход, оказывается, результативный и эффективный.
Введение: С роботом дуговой сварки, программирование дорожки инструмента обычно выполняется в двух шагах. Сначала, сварочный шнур - дискретизируется в ряд трехмерных поз - то есть. положение и ориентация, каждый описываемый вектором положения p наконечника инструмента относительно происхождения части создает и вектор единицы, а именно, q, по оси инструмента и указывающий к держащему концу инструмент, оба выражены в структуре . Во вторых, этот набор трехмерных поз нанесен на декартовую систему координат, чтобы соединить место с обратной кинематической моделью сварочного робота.
Проблема планирования траектории может быть решена через вычисление вектора Dar-boux дорожки и ее производной времени, которая также предписывает угловую скорость и ускорение сварочного инструмента относительно . Как показано в [1], этот подход требует, вычисление тангенса, нормального и бинормального векторов данной дорожки инструмента, и затем решить обратную кинематическую проблему для каждого вычисления триады. Хотя дорожка инструмента, являющаяся непрерывной в декартовой системе, но с этим подходом, его соответствующая дорожка в объединенном месте, возможно, не непрерывна.
Кроме того, отмечено, что ориентация инструмента вокруг оси электрода является несоответствующей сварочной операции, и следовательно, эта задача может быть выполнена с только "пятью степенями свободы". Однако, если задача выполнена роботом с шестью СС, есть одна СС избыточная, и возможно осуществить вторичную стратегию контроля, как предотвращение пределов предотвращения в сочленениях.
Формулировка Проблемы: Этот предмет решения избыточности был уже изучен и на уровне
объединенного положения [2, 3] и на уровне объединенной нормы [4, 5]. Здесь, мы
принимаем формулировку объединенной нормы, потому что проблема решения избыточности
линейна на том уровне. Якобиан шести СС сварочного робота, а именно, J, наносит на
карту норму соединения 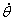 в завихрение t сварочного
инструмента следующим образом:
в завихрение t сварочного
инструмента следующим образом:
|
|
(1) |
где 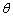 и t определены как
и t определены как
|
|
(2) |
с  и
и  соответственно угловыми и переводными скоростями сварочного инструмента относительно
исходного и выраженного в . Есть два различных подхода осуществить задачу с пятью
СС, используя шестую СС завихрение. Сначала, можно спроектировать первые три линии J
и первой части t, то есть , на перпендикуляр плана к оси электрода. С этим подходом,
обратная кинематическая проблема уменьшает до определения объединенных норм
спроектированного якобиана на спроектированное завихрение. Однако, проекторы всегда
исключительны и следовательно, специфическая структура проектирования должна
быть принята во внимание, решение для спроектированного якобиана. Второй подход
принимает действительное вращение, а именно,
соответственно угловыми и переводными скоростями сварочного инструмента относительно
исходного и выраженного в . Есть два различных подхода осуществить задачу с пятью
СС, используя шестую СС завихрение. Сначала, можно спроектировать первые три линии J
и первой части t, то есть , на перпендикуляр плана к оси электрода. С этим подходом,
обратная кинематическая проблема уменьшает до определения объединенных норм
спроектированного якобиана на спроектированное завихрение. Однако, проекторы всегда
исключительны и следовательно, специфическая структура проектирования должна
быть принята во внимание, решение для спроектированного якобиана. Второй подход
принимает действительное вращение, а именно, 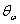 ,
наконечника инструмента вокруг оси электрода. Хотя это вращение не существует, это
добавлено к якобиану и объединенной норме, чтобы получить недоопределённый линейную
алгебраическую систему по крайней мере с одной избыточной СС. Этот второй подход
предпочтен, так как он является очень простым, чем первый.
,
наконечника инструмента вокруг оси электрода. Хотя это вращение не существует, это
добавлено к якобиану и объединенной норме, чтобы получить недоопределённый линейную
алгебраическую систему по крайней мере с одной избыточной СС. Этот второй подход
предпочтен, так как он является очень простым, чем первый.
Якобиан робота, увеличенного действительной объединенной нормой
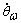 вокруг сварочной оси инструмента, а
именно,
вокруг сварочной оси инструмента, а
именно,  наносит на карту
увеличенный собственный вес
наносит на карту
увеличенный собственный вес 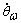 нормы
соединения в завихрение t сварочного инструмента как
нормы
соединения в завихрение t сварочного инструмента как
|
|
(3) |
где 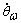 определен как
определен как
|
|
(4) |
Стратегия предотвращения пределов перемещения в сочленениях: решение уравнения (3) известно, и вычисляется как
|
|
(5) |
с h вторичной задачей и 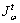 правой обобщенной инверсией
правой обобщенной инверсией  ,
т.е.
,
т.е. 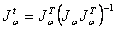 . Кроме того,
. Кроме того,
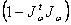 - ортогональное дополнение
- ортогональное дополнение
 проектирующий h в зону
нечувствительности
проектирующий h в зону
нечувствительности  . Таким образом
. Таким образом
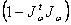 h - гомогенное решение уравнения (3),
которое соответствует самопроизвольному движению
h - гомогенное решение уравнения (3),
которое соответствует самопроизвольному движению  ,
то есть, движение
,
то есть, движение 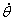 и
и
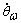 , под которым наконечник инструмента остается
постоянным относительно части. Так как
, под которым наконечник инструмента остается
постоянным относительно части. Так как 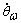 только
действителен, самопроизвольное движение
только
действителен, самопроизвольное движение  эквивалентно движению
эквивалентно движению 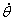 , под которым
указывается положение и только ориентация оси инструмента остаются постоянными
относительно части.
, под которым
указывается положение и только ориентация оси инструмента остаются постоянными
относительно части.
Вторичная задача выбрана как h=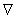 z,
где z определена как следующая объективная функция, а именно,
z,
где z определена как следующая объективная функция, а именно,
|
|
(6) |
где W - положительно-определенная матрица надбавки, и
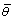 вычислена как середина двух
объединенного положения робота, вычисленная как
вычислена как середина двух
объединенного положения робота, вычисленная как
|
|
(7) |
или среднее-объединенное положение робота по сварочной дорожке инструмента A, то есть,
|
|
(8) |
где t - время. Ясно, эта задача оптимизация позволяет наконечник инструмента и ось оставлять на сварочной дорожке инструмента, сохраняя позицию совместных параметров робота в самом близком интервале или от середины совместной позиции или от среднего объединенного положения робота. Матрица надбавки W выбрана как диагональная матрица, элементы которой определены допустимыми отклонениями от этой середины - или среднего- объединенного положения.
Числовая реализация: В этой статье, мы используем схему ортогонализации, предложенную
Arenson и др. [6], чтобы передать  в более-низкой
треугольной форме, сохраняя ее число состояний. В этом подходе, решение избыточности
вычислено, не требуя прямого вычисления обобщенной инверсии
в более-низкой
треугольной форме, сохраняя ее число состояний. В этом подходе, решение избыточности
вычислено, не требуя прямого вычисления обобщенной инверсии  ,
и следовательно, избегается возведения в квадрат числа условия
проблемы. Мы вспоминаем, что число условий проблемы выражает потерю точности в течение
ее решения. Для контроля сварочных операций, возведение в квадрат ошибок очевидно недопустимо.
,
и следовательно, избегается возведения в квадрат числа условия
проблемы. Мы вспоминаем, что число условий проблемы выражает потерю точности в течение
ее решения. Для контроля сварочных операций, возведение в квадрат ошибок очевидно недопустимо.
Применение сварки при наземной прокладке трубопровода: Стратегия была осуществлена в пределах
модуля моделирования и проверена с контсрукцией манипулятора Puma-560 вместе с родовым
инструментом дуговой сварки, типа описываемого параметрами Denavit-Hartenbrg приведённых
в таб. 1. Для быстрой ссылки, мы коротко вспоминаем значение этих параметров ниже. Позвольте
нам прилагать структуру Fi чтобы связать i с zi-осью, переходя к оси соединения
i + 1, и xi-ось выравнивала по общему перпендикуляру к параметрам соединения i и i + 1.
Первый параметр 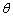 i - объединенное вращение вокруг
zi-оси; bi - расстояние перевода по zi-оси положения Fi
к общему перпендикуляру с Fi+1; ai - длина этого общего перпендикуляра;
в то время как
i - объединенное вращение вокруг
zi-оси; bi - расстояние перевода по zi-оси положения Fi
к общему перпендикуляру с Fi+1; ai - длина этого общего перпендикуляра;
в то время как 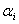 - вращение вокруг общего перпендикуляра к Fi+1.
- вращение вокруг общего перпендикуляра к Fi+1.
Примечательно, что таблица 1 включает действительное седьмое соединение, а именно,
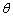 7, которое очевидно не существует, и таким образом,
не управляется роботом. Цель этого седьмого соединения состоит в том, чтобы описать выгоду свободы
задачи из-за использования симметрического электрода. Контроль этого действительного 7 СС робота по
полностью принужденной 6 СС задаче с
7, которое очевидно не существует, и таким образом,
не управляется роботом. Цель этого седьмого соединения состоит в том, чтобы описать выгоду свободы
задачи из-за использования симметрического электрода. Контроль этого действительного 7 СС робота по
полностью принужденной 6 СС задаче с  эквивалентный управлению
первоночальным 6 СС робота по 5 СС сварочной задаче с
эквивалентный управлению
первоночальным 6 СС робота по 5 СС сварочной задаче с  .
В обоих случаях, робот имеет одну СС больше чем задача, и следовательно, там является одним СС из
избыточности, чтобы решить со стратегией предотвращения пределов перемещения в суставах.
.
В обоих случаях, робот имеет одну СС больше чем задача, и следовательно, там является одним СС из
избыточности, чтобы решить со стратегией предотвращения пределов перемещения в суставах.
Таблица 1: параметры Denavit-Hartenberg Пумы 560 с общим сварочным инструментом
| соединение |
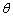 i i
|
ai | bi |
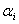
|
| 1 |
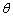 1 1
|
0.0 | 0.0 |
-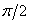
|
| 2 |
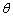 2 2
|
0.4318 | 0.0 | 0.0 |
| 3 |
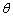 3 3
|
-0.0203 | 0.1491 |
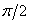
|
| 4 |
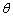 4 4
|
0.0 | 0.4330 |
-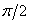
|
| 5 |
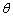 5 5
|
0.0 | 0.0 |
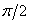
|
| 6 |
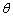 6 6
|
0.0 | 0.7294 |
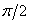
|
| 7 |
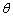 7 7
|
0.0 | -0.2000 | 0.0 |
| номер | рад. | м | м | рад |
Робот нацелен, чтобы выполнить сварку траектории при прокладке трубопровода за T = 280sec, то есть,
 , ,
|
(9) |
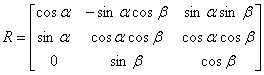 ,
,
где:
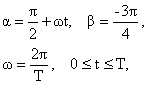 , ,
|
(10) |
где расстояния и углы,соответственно, выражены в метрах и радианах.
Рисунок 1 показывает историю времени объединенных положений робота по данной сварочной траектории, не принимая во внимание симметрию сварочного электрода. Соответствующая история времени задачи робота иллюстрирована на рис. 4. Очевидно, робот в состоянии выполнить задачу, используя полную амплитуду ее объединенного движения. Второй последовательный поворот, очевидно, не возможен, не превышая объединенные пределы.
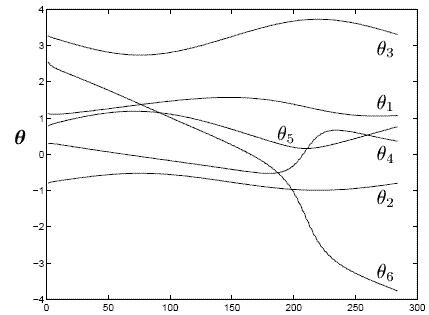
Рис. 1 - Объединенные положения без стратегии предотвращения объединенных пределов
Рисунок 2 показывает историю времени объединенных положений робота по той же самой
траектории, но контроль выполнен с увеличенным якобианом и вектором объединенной нормы
вместе с серединой объединенной стратегии робота, с 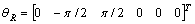 .
Соответствующая история времени
задачи робота иллюстрирована в рис. 5. Очевидно, робот в состоянии выполнить задачу,
используя намного меньше амплитуды ее объединенного движения. Здесь снова, второй
последовательный поворот не возможен, не превышая объединенные пределы.
.
Соответствующая история времени
задачи робота иллюстрирована в рис. 5. Очевидно, робот в состоянии выполнить задачу,
используя намного меньше амплитуды ее объединенного движения. Здесь снова, второй
последовательный поворот не возможен, не превышая объединенные пределы.
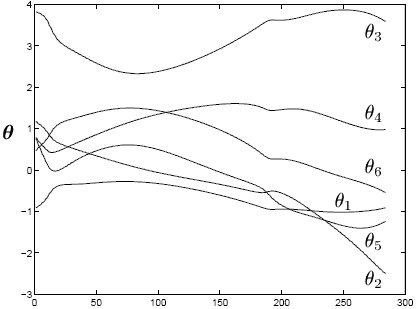
Рис. 2 - Объединенные положения с серединой объединенной стратегии предотвращения
Рисунок 3 показывает историю времени объединенных положений робота по той же самой
траектории, контроль здесь выполнен с увеличенным якобианом и вектором объединенной
нормы вместе со средней-объединенной стратегией робота, с 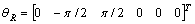 .
Соответствующая история
времени задачи робота иллюстрирована в рис. 6. Очевидно, робот все еще в состоянии
выполнить задачу, используя приблизительно ту же самую амплитуду ее объединенного
движения. Кроме того, многократные последовательные повороты здесь возможны, не превышая
пределов предотвращения в сочленениях, и следовательно, циклическая траектория возможна
с этой стратегией. Фактически, робот начинает и заканчивает круглую траекторию точно
теми же самыми объединенными положениями.
.
Соответствующая история
времени задачи робота иллюстрирована в рис. 6. Очевидно, робот все еще в состоянии
выполнить задачу, используя приблизительно ту же самую амплитуду ее объединенного
движения. Кроме того, многократные последовательные повороты здесь возможны, не превышая
пределов предотвращения в сочленениях, и следовательно, циклическая траектория возможна
с этой стратегией. Фактически, робот начинает и заканчивает круглую траекторию точно
теми же самыми объединенными положениями.
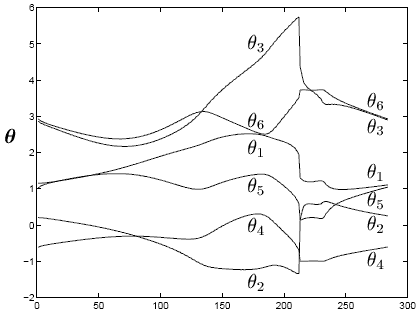
Рис. 3 - Объединенные положения со средней-объединенной стратегией предотвращения
Ясно, получающаяся траектория в объединенном месте с серединой объединенной стратегии
предотвращения (то есть  ) зависит от относительного
положения и ориентации агрегата относительно середины объединенного положения. Смещение
агрегата значительно изменяет циклическую или нециклическую природу получающейся траектории
в объединенном месте. Наоборот, средняя-объединенная стратегия предотвращения (то есть,
) зависит от относительного
положения и ориентации агрегата относительно середины объединенного положения. Смещение
агрегата значительно изменяет циклическую или нециклическую природу получающейся траектории
в объединенном месте. Наоборот, средняя-объединенная стратегия предотвращения (то есть,
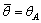 ) позволяет держать
циклическую природу траектории в объединенном пространстве траектории. Однако, смещение
блока в пределах рабочее пространство робота не даёт гарантию способности робота выполнить
траекторию в объединенном месте, не превышая пределы перемещения в сочленениях. Фактически,
выбор положения и ориентации собрания приводит к среднему- объединенному положению, которое
должно быть так близко насколько возможно к середине объединенного положения, чтобы уменьшить
до минимума вероятность превышения объединенных пределов. Таким образом, оптимальные положения
и ориентации агрегата - те, которые являются решениями следующего уравнения, то есть,
) позволяет держать
циклическую природу траектории в объединенном пространстве траектории. Однако, смещение
блока в пределах рабочее пространство робота не даёт гарантию способности робота выполнить
траекторию в объединенном месте, не превышая пределы перемещения в сочленениях. Фактически,
выбор положения и ориентации собрания приводит к среднему- объединенному положению, которое
должно быть так близко насколько возможно к середине объединенного положения, чтобы уменьшить
до минимума вероятность превышения объединенных пределов. Таким образом, оптимальные положения
и ориентации агрегата - те, которые являются решениями следующего уравнения, то есть,
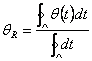 , ,
|
(11) |
для данной траектории свободной А, необходимо чтобы перевести и вращаться, вперед и вокруг, любую ось.
Заключения: стратегия предотвращения пределов перемещения в сочленениях была представлена для операций дуговой сварки, где добавляется одна СС из-за симметрии электрода относительно к его оси. В этой ситуации, сварочная задача может быть выполнена роботами только с пятью СС. Однако, когда выполнено роботами с шестью СС, возможно осуществить стратегию предотвращения пределов соединения на увеличенной якобиевской матрице и увеличенном векторе объединенной нормы действительным седьмым вращением вокруг оси электрода. С этим увеличенным подходом, возможно найти циклическую траекторию в объединенном месте, которая избегает объединенных пределов под надлежащим местоположением агрегата в пределах рабочего пространства робота.
Подтверждение: финансовая поддержка от Естественных наук и Проектирующий Совет Исследования Канады под предоставлением OGPIN-203618 с благодарностью признана.
Биография
| Реферат
| Библиотека
| Отчет о поиске
| Ссылки
| Задание