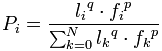
Существует две основные области исследований систем баз данных. Одна из них – это анализ моделей данных, на которые может отображаться реальный мир и на основе которых могут строиться интерфейсы для различных типов пользователей. Такие концептуальные модели включают иерархическую, сетевую, реляционную модели, а также ряд моделей, ориентированных на семантику.
Вторая область затрагивает безопасную и эффективную реализацию СУБД (систем управления баз данных). Компьютеризированные данные становятся центральным ресурсом большинства организаций. Это должно учитываться в каждой реализации, предназначенной для производственного использования, путем гарантирования безопасности данных в случаях параллельного доступа, восстановления и реорганизации. Одно из основных критических замечаний ко многим ранним СУБД относилось к отсутствию эффективности при обработке предлагаемых ими мощных операций, в особенности, доступа к данным на основе их содержимого через запросы. Оптимизация запросов предназначена для решения этой проблемы путем интеграции большого числа методов и стратегий, простирающихся от логических преобразований запросов до оптимизации путей доступа и хранения данных на уровне файловых систем.
Проблема оптимизации запросов требует решения следующих задач:
Преобразование запроса к более эффективному непроцедурному представлению (логическая оптимизация).
Выбор набора альтернативных процедурных планов выполнения запроса.
Оценка стоимости выполнения запроса по выбранному плану и т.д.
Для каждой задачи существует более одного подхода к их решению. Например, проблемы, связанные с логической оптимизацией запросов, породили направление, называемое семантической оптимизацией [1]. Очень многие исследователи заняты проблемами оценок стоимости процедурных планов выполнения запросов (и до сих пор вопрос о достоверности оценок до конца не ясен) [2].
Особенно много исследований в последние годы посвящается оптимизации запросов и выбору эффективных способов выполнения реляционных операций в распределенных реляционных системах управления базами данных [3]. Здесь существует очень много вариантов и физической организации распределенных баз данных (с поддержкой копий отношений в нескольких узлах сети, с горизонтальным или вертикальным разделением отношений в нескольких узлах, с поддержкой мгновенных снимков базы данных и т.д.), и алгоритмов выполнения реляционных операций при каждой такой организации.
Цели работы:
Разработка модели системы выбора оптимального глобального плана распределённого запроса.
Исследование и выбор параметров этой системы.
Разработка алгоритма на основе муравьиных колоний для определения наиболее оптимального глобального плана запроса.
Оптимизация запросов к базе данных является наиболее важным и интересным направлением исследований и разработок во всей области баз данных. Важность этого направления определяется тем, что от развитости компонента оптимизации запросов критически зависит общая производительность любой SQL-ориентированной СУБД. Это направление наиболее интересно, потому что при решении задач оптимизации можно использовать самые разнообразные подходы и методы из различных областей вычислительной науки и математики: методы оптимизации программ, применяемые в компиляторах языков программирования, математическую логику, математическую статистику, методы искусственного интеллекта, распознавания образов и т.д.
Большинство современных оптимизаторов используют метод полного перебора для формирования и выбора оптимального глобального плана распределённого запроса. Для небольших распределённых БД (баз данных) это оправданно, т.к. само количество возможных вариантов не так уж и велико. Однако в последнее время набирают популярность распределённые системы с большим количеством узлов (например, облачные технологии), для которых полный перебор всех вариантов может существенно сказаться на производительности.
Актуальность этой работы состоит в использовании алгоритма, не осуществляющего полный перебор, но при этом возвращающего один из наиболее оптимальных результатов.
Научная новизна:
На основе модели графа операций (переходов) разработана уникальная графовая модель процесса оптимизации глобального запроса. В процессе выполнения магистерской работы будут исследованы её параметры.
Впервые применён муравьиный алгоритм для решения задачи оптимизации запросов.
В результате работы планируется получить приложение, которое находит оптимальный глобальный план запроса для заданных серверов и таблиц БД, а также затрат на соединение с серверами.
Большинство исследований в данной области не продвинулись дальше теоретического уровня. Стоит выделить работы руководителя исследовательских работ в Microsoft Research Сураджита Чаудхари [4], Матиаса Ярке и Юргена Коха [5], Сергея Кузнецова [6]. В некоторых исследованиях предлагаются механизмы динамической обработки запросов, такие как eddy [7]. В пределах ДонНТУ исследования в сфере распределённых БД и систем обработки данных проводились магистрами Подлесной Я.И. [8], Барановой С.С. [9], Шегалем Е.И. [10]. Также в этой магистерской работе были использованы материалы Керенцевой М.А., Савковой Е.О., Мартыненко Т.В. [11].
Среди реализованных систем можно отметить систему TinyDB, оптимизатор которой учитывает энергопотребление.
Для поиска оптимального пути по графу можно применить такие алгоритмы, как:
Основной недостаток этих алгоритмов – в том, что фактически они используют метод полного перебора.
Муравьиный алгоритм (алгоритм оптимизации подражанием муравьиной колонии, англ. ant colony optimization, ACO) — один из эффективных полиномиальных алгоритмов для нахождения приближённых решений задачи коммивояжёра, а также аналогичных задач поиска маршрутов на графах. Суть подхода заключается в анализе и использовании модели поведения муравьёв, ищущих пути от колонии к источнику питания и представляет собой метаэвристическую (англ. metaheuristic, meta — «за пределами» и heuristic — «найти») оптимизацию. Первая версия алгоритма, предложенная доктором наук Марко Дориго в 1992 году, была направлена на поиск оптимального пути в графе.
В основе алгоритма лежит поведение муравьиной колонии — маркировка более удачных путей большим количеством феромона. Работа начинается с размещения муравьёв в вершинах графа (городах), затем начинается движение муравьёв — направление определяется вероятностным методом, на основании формулы вида:
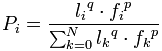
где: Pi – вероятность перехода по пути i, li – величина, обратная весу (длине) i-ого перехода, fi – количество феромона на i-ом переходе, q – величина, определяющая «жадность» алгоритма, p – величина, определяющая «стадность» алгоритма и q + p = 1. Обновление феромонов происходит согласно формуле: 
i, j = (1 - 
)i, j +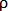 
i, j, где i, j — количество феромона на дуге i,j, 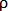— скорость испарения феромона, i, j — количество отложенного феромона, обычно определяется как
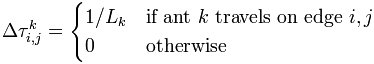
где Lk — стоимость k-го пути муравья (обычно длина).
Решение не является точным и даже может быть одним из худших, однако, в силу вероятностности решения, повторение алгоритма может выдавать достаточно точный результат. В реальном мире муравьи (первоначально) ходят в случайном порядке и по нахождению продовольствия возвращаются в свою колонию, прокладывая феромонами тропы. Если другие муравьи находят такие тропы, они, вероятнее всего, пойдут по ним. Вместо того, чтобы отслеживать цепочку, они укрепляют её при возвращении, если в конечном итоге находят источник питания. Со временем феромонная тропа начинает испаряться, тем самым уменьшая свою привлекательную силу. Чем больше времени требуется для прохождения пути до цели и обратно, тем сильнее испарится феромонная тропа. На коротком пути, для сравнения, прохождение будет более быстрым и как следствие, плотность феромонов остаётся высокой. Испарение феромонов так же имеет свойство избежания, стремления к локально-оптимальному решению. Если бы феромоны не испарялись, то путь, выбранный первым, был бы самым привлекательным. В этом случае, исследования пространственных решений были бы ограниченными. Таким образом, когда один муравей находит (например, короткий) путь от колонии до источника пищи, другие муравьи, скорее всего пойдут по этому пути, и положительные отзывы в конечном итоге приводят всех муравьёв к одному, кратчайшему, пути.
Оригинальная идея исходит от наблюдения за муравьями в процессе поиска кратчайшего пути от колонии до источника питания и проиллюстрирована на рисунке ниже.
Первый муравей находит источник пищи (F) любым способом (а), а затем возвращается к гнезду (N), оставив за собой тропу из феромонов (b).
Затем муравьи выбирают один из четырёх возможных путей, затем укрепляют его и делают привлекательным.
Муравьи выбирают кратчайший маршрут, так как у более длинных феромоны сильнее испарились.
Среди экспериментов по выбору между двумя путями неравной длины, ведущих от колонии к источнику питания, биологи заметили, что, как правило, муравьи используют кратчайший маршрут. Модель такого поведения заключается в следующем:
Муравьи используют окружающую среду как средство общения. Они обмениваются информацией косвенным путём, через феромоны, в ходе их «работы». Обмен информации имеет локальный характер, только те муравьи, которые находятся в непосредственной близости, где остались феромоны — могут узнать о них. Такая система называется «Stigmergy» и справедлива для многих социальных животных (была изучена в случае строительства столбов в гнёздах термитов). Данный механизм решения проблемы очень сложен и является хорошим примером самоорганизации системы. Такая система базируется на положительной (другие муравьи укрепляют феромонную тропу) и отрицательной (испарение феромонной тропы) обратной связи. Теоретически, если количество феромонов будет оставаться неизменным, с течением времени, по всем маршрутам, невозможно будет выбрать путь. Однако из-за обратной связи, небольшие колебания приведут к усилению одного из маршрутов и система стабилизируется к кратчайшему пути.
На момент написания реферата выполнены следующий цели:
Оптимизаторы реляционных СУБД представляют собой наиболее сложные компоненты систем. Эффективность системы в целом во многом определяется тем, насколько мощной является оптимизация. Во всех существующих направлениях, связанных с оптимизацией, остается множество нерешенных проблем. Большинство из них имеют переборный характер и требуют развитых эвристических решений.
Большей частью в стороне остались проблемы оптимизации, возникающие при использовании специализированной аппаратуры машин баз данных, где главное внимание уделяется возможностям распараллеливания выполнения запросов. Спектр возможных архитектур машин баз данных достаточно широк, и проблемы оптимизации имеют свою специфику для каждой из конкретных архитектур.
Другая специфическая проблема оптимизации запросов и структур хранения и стратегий доступа относится к системам управления базами данных в оперативной памяти. Такие системы становятся все более актуальными в связи с постоянным увеличением объемов доступной в ЭВМ оперативной памяти и ее удешевлением. Особенно интересны возможности использования оперативной памяти, сохраняющей информацию после выключения питания. Если удастся добиться удешевления и этого вида аппаратуры, могут наступить революционные изменения в подходах к организации и баз данных, и систем управления ими с соответствующим смещением акцентов в области оптимизации.
Тем не менее, в ближайшие годы, скорее всего, наиболее распространены будут по-прежнему системы управления базами данных, хранимыми в традиционно организованной внешней памяти. Поэтому и традиционные оптимизаторы еще долго будут сохранять свою актуальность.
Chakravarthy U.S., Fishman D.H., Minker J. Semantic Query Optimization in Expert Systems and Database Systems // Expert Database Syst.: Proc. 1st Int. Workshop, Menlo Park, Calif., Feb. 1986. New York, 1986.– c. 326-341
Yao S.B. Approximating Block Acess in Database Organizations // Commun. ACM.– 1977.– 20, N 4.– c. 260-261
Lohman G.M., Daniels D., Haas L.M., Kistler R., Selinger P.G. Optimization of Nested Queries in a Distributed Relational Database // Proc. 10th Int. Conf. Very Large Data Bases, Singapore, Aug. 27-31, 1984. New York, 1984.
Методы оптимизации запросов в реляционных системах [электронный ресурс]. – Режим доступа: http://www.sdteam.com/t1951
Оптимизация запросов в системах баз данных [электронный ресурс]. – Режим доступа: http://citforum.ru/.../query_optimization/
Методы оптимизации выполнения запросов в реляционных СУБД [электронный ресурс]. – Режим доступа: http://citforum.ru/.../art_26.shtml
Eddies: Continuously Adaptive Query Processing [электронный ресурс]. – Режим доступа: http://db.cs.berkeley.edu/papers/sigmod00-eddy.pdf
Динамическая оптимизация распределения данных по узлам сети [электронный ресурс]. – Режим доступа: http://masters.donntu.ru/.../index.htm
Динамическая оптимизация распределения данных по узлам вычислительной сети [электронный ресурс]. – Режим доступа: http://masters.donntu.ru/.../index.htm
Исследование свойств распределенных систем обработки данных [электронный ресурс]. – Режим доступа: http://masters.donntu.ru/.../index.htm
Разработка графо-аналитической модели учета нагрузок веб-базированных систем [электронный ресурс]. – Режим доступа: http://masters.donntu.ru/.../article2.htm