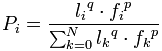
Існує дві основні області досліджень систем баз даних. Одна з них – це аналіз моделей даних, на які може відображатися реальний світ і на основі яких можуть будуватися інтерфейси для різних типів користувачів. Такі концептуальні моделі включають ієрархічну, мережеву, реляційну моделі, а також ряд моделей, орієнтованих на семантику.
Друга область стосується безпечної і ефективної реалізації СУБД. Комп'ютеризовані дані стають центральним ресурсом більшості організацій. Це повинно враховуватися в кожній реалізації, призначеної для виробничого використання, шляхом гарантування безпеки даних у випадках паралельного доступу, відновлення і реорганізації. Одне з основних критичних зауважень до багатьох ранніх СУБД відносилося до відсутності ефективності при обробці пропонованих ними потужних операцій, особливо, доступу до даних на основі їх вмісту через запити. Оптимізація запитів призначена для вирішення цієї проблеми шляхом інтеграції великого числа методів і стратегій, що тягнуться від логічних перетворень запитів до оптимізації шляхів доступу та зберігання даних на рівні файлових систем.
Проблема оптімизації запросів потребує рішення наступних задач:
Перетворення запиту до більш ефективного непроцедурного представлення (логічна оптимізація).
Вибір набору альтернативних процедурних планів виконання запиту.
Оцінка вартості виконання запиту за обраним планом і т.д.
Для кожної задачі існує більше одного підходу до їх вирішення. Наприклад, проблеми, пов'язані з логічною оптимізацією запитів, породили напрямок, який називається семантичної оптимізацією [1]. Дуже багато дослідників зайняті проблемами оцінок вартості процедурних планів виконання запитів (і до цих пір питання про достовірність оцінок до кінця не ясне) [2].
Особливо багато досліджень в останні роки присвячується оптимізації запитів і вибору ефективних способів виконання реляційних операцій в розподілених реляційних системах управління базами даних [3]. Тут існує дуже багато варіантів і фізичної організації розподілених баз даних (з підтримкою копій відносин в декількох вузлах мережі, з горизонтальним або вертикальним поділом відносин в декількох вузлах, з підтримкою миттєвих знімків бази даних і т.д.), і алгоритмів виконання реляційних операцій при кожної такої організації.
Цілі роботы:
Розробка модели системы вибору оптимального глобального плану розподіленого запиту.
Дослідження і вибір параметрів цієї системи.
Розробка алгоритму на основі мурашиных колоній для визначення найбільш оптимального глобального плану запиту.
Оптимізація запитів до бази даних є найбільш важливим і цікавим напрямком досліджень і розробок у всій області баз даних. Важливість цього напрямку визначається тим, що від розвиненості компонента оптимізації запитів критично залежить загальна продуктивність будь-який SQL-орієнтованої СУБД. Цей напрям найбільш цікавий, тому що при вирішенні задач оптимізації можна використовувати найрізноманітніші підходи та методи з різних областей обчислювальної науки і математики: методи оптимізації програм, що застосовуються в компіляторах мов програмування, математичну логіку, математичну статистику, методи штучного інтелекту, розпізнавання образів і т . д.
Більшість сучасних оптимізаторів використовують метод повного перебору для формування та вибору оптимального глобального плану розподіленого запиту. Для невеликих розподілених БД це виправдано, тому що сама кількість можливих варіантів не таке вже і велике. Проте останнім часом набирають популярність розподілені системи з великою кількістю вузлів (наприклад, хмарні технології), для яких повний перебір всіх варіантів може значно позначитися на продуктивності.
Актуальність цієї роботи полягає у використанні алгоритму, який не здійснює повний перебір, але при цьому повертає один з найбільш оптимальних результатів.
Наукова новизна:
На основі моделі графа операцій (переходів) розроблена унікальна графова модель процесу оптимізації глобального запиту. В процесі виконання магістерської роботи будуть досліджені її параметри.
Вперше застосовано мурашиний алгоритм для вирішення задачі оптимізації запитів.
В результаті роботи планується отримати програму, яка знаходить оптимальний глобальний план запиту для заданих серверів і таблиць БД, а також витрат на з'єднання з серверами.
Більшість досліджень в даній області не просунулися далі теоретичного рівня. Варто виділити роботи керівника дослідницьких робіт у Microsoft Research Сураджита Чаудхарі [4], Матіаса Ярке та Юргена Коха [5], Сергія Кузнецова [6]. В деяких дослідженнях пропонуються механізми динамічної обробки запитів, такі як eddy [7]. В межах ДонНТУ дослідження у сфері розподілених БД та систем обробки даних проводилися магістрами Підлісної Я.І. [8], Барановою С.С. [9], Шегалєм Є.І. [10]. Також у цій магістерській роботі були використані матеріали Керенцевой М.А., Савковой Е.О., Мартиненко Т.В. [11].
Серед реалізованих систем можна відзначити систему TinyDB, оптимізатор якої враховує енергоспоживання.
Для пошуку оптимального шляху по графу можна застосувати такі алгоритми, як:
Основний недолік цих алгоритмів – в тому, що фактично вони використовують метод повного перебору.
Мурашиний алгоритм (алгоритм оптимізації наслідуванням мурашиної колонії, англ. ant colony optimization, ACO) – один з ефективних поліноміальних алгоритмів для знаходження наближених рішень задачі комівояжера, а також аналогічних завдань пошуку маршрутів на графах. Суть підходу полягає в аналізі та використанні моделі поведінки мурах, що шукають шляхи від колонії до джерела живлення і являє собою метаевристичну (англ. metaheuristic, meta – «за межами» і heuristic – «знайти») оптимізацію. Перша версія алгоритму, запропонована доктором наук Марко Доріго в 1992 році, була спрямована на пошук оптимального шляху в графі.
В основі алгоритму лежить поведінка мурашиної колонії – маркування більш вдалих шляхів великою кількістю феромона. Робота починається з розміщення мурашок у вершинах графа (містах), потім починається рух мурашок – напрям визначається імовірнісним методом, на підставі формули виду:
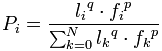
де: Pi – ймовірність переходу по шляху i, li – величина, зворотна вазі (довжині) i-ого переходу, fi – кількість феромонів на i-му переході, q – величина, що визначає «жадібність» алгоритму, p – величина, що визначає «стадність» алгоритму і q + p = 1. Оновлення феромонів відбувається згідно з формулою: 
i, j = (1 - 
) i, j +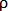 
i, j, де i, j – кількість феромонів на дузі i, j, 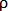– швидкість випаровування феромону, i, j – кількість відкладеного феромона, зазвичай визначається як
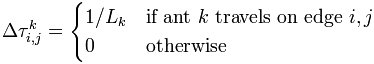
де Lk — вартість k-го шляху мурахи (зазвичай довжина).
Рішення не є точним і навіть може бути одним з гірших, проте, через імовірнісність рішення, повторення алгоритму може видавати досить точний результат. У реальному світі мурашки (спочатку) ходять у випадковому порядку і після знаходження продовольства повертаються у свою колонію, прокладаючи феромонами стежки. Якщо інші мурахи знаходять такі стежки, вони, найімовірніше, підуть за ними. Замість того, щоб відстежувати ланцюжок, вони зміцнюють його при поверненні, якщо в кінцевому підсумку знаходять джерело живлення. З часом феромонна стежка починає випаровуватися, тим самим зменшуючи свою привабливу силу. Чим більше часу потрібно для проходження шляху до мети і назад, тим сильніше випарується феромонна стежка. На короткому шляху, для порівняння, проходження буде більш швидким і як наслідок, щільність феромонів залишається високою. Випаровування феромонів так само має властивість уникнення, прагнення до локально-оптимального рішення. Якби феромони не випаровувалися, то шлях, обраний першим, був би самим привабливим. У цьому випадку, дослідження просторових рішень були б обмеженими. Таким чином, коли одна мураха знаходить (наприклад, короткий) шлях від колонії до джерела їжі, інші мурахи, швидше за все підуть цим шляхом, і позитивні відгуки в кінцевому підсумку призводять всіх мурах до одного, найкоротшого, шляху.
Оригінальна ідея виходить від спостереження за мурахами в процесі пошуку найкоротшого шляху від колонії до джерела живлення і проілюстрована на малюнку нижче.
Перша мураха знаходить джерело їжі (F) будь-яким способом (а), а потім повертається до гнізда (N), залишивши за собою стежку з феромонів (b).
Потім мурахи вибирають один з чотирьох можливих шляхів, потім зміцнюють його і роблять привабливим.
Мурахи вибирають найкоротший маршрут, так як у більш довгих феромони сильніше випарувалися.
Серед експериментів з вибору між двома шляхами нерівної довжини, що ведуть від колонії до джерела живлення, біологи помітили, що, як правило, мурашки використовують найкоротший маршрут. Модель такої поведінки полягає в наступному:
Мурахи використовують навколишнє середовище як засіб спілкування. Вони обмінюються інформацією непрямим шляхом, через феромони, в ході їх «роботи». Обмін інформацією має локальний характер, тільки ті мурахи, які знаходяться в безпосередній близькості, де залишилися феромони – можуть дізнатися про них. Така система називається «Stigmergy» і справедлива для багатьох соціальних тварин (була вивчена у випадку будівництва стовпів в гніздах термітів). Даний механізм вирішення проблеми дуже складний і є гарним прикладом самоорганізації системи. Така система базується на позитивній (інші мурахи зміцнюють феромонну стежку) і негативною (випаровування феромонної стежки) зворотного зв'язку. Теоретично, якщо кількість феромонів буде залишатися незмінною, з плином часу, по всіх маршрутах, неможливо буде вибрати шлях. Однак через зворотній зв'язок, невеликі коливання призведуть до посилення одного з маршрутів, і система стабілізується до найкоротого шляху.
На момент написання реферату виконані наступний цілі:
Оптимізатори реляційних СУБД являють собою найбільш складні компоненти систем. Ефективність системи в цілому багато в чому визначається тим, наскільки потужною є оптимізація. У всіх існуючих напрямках, пов'язаних з оптимізацією, залишається безліч невирішених проблем. Більшість з них мають перебірний характер і вимагають розвинених евристичних рішень.
Здебільшого в стороні залишилися проблеми оптимізації, що виникають при використанні спеціалізованої апаратури машин баз даних, де головна увага приділяється можливостям розпаралелювання виконання запитів. Спектр можливих архітектур машин баз даних досить широкий, і проблеми оптимізації мають свою специфіку для кожної з конкретних архітектур.
Інша специфічна проблема оптимізації запитів і структур зберігання і стратегій доступу відноситься до систем управління базами даних в оперативній пам'яті. Такі системи стають все більш актуальними у зв'язку з постійним збільшенням обсягів доступної в ЕОМ оперативної пам'яті і її здешевленням. Особливо цікаві можливості використання оперативної пам'яті, що зберігає інформацію після виключення живлення. Якщо вдасться добитися здешевлення і цього виду апаратури, можуть наступити революційні зміни в підходах до організації і баз даних, і систем управління ними з відповідним зміщенням акцентів у галузі оптимізації.
Тим не менш, у найближчі роки, швидше за все, найбільш поширені будуть як і раніше системи управління базами даних, що зберігаються в традиційно організованою зовнішньої пам'яті. Тому й традиційні оптимізатори ще довго будуть зберігати свою актуальність.
Chakravarthy U.S., Fishman D.H., Minker J. Semantic Query Optimization in Expert Systems and Database Systems // Expert Database Syst.: Proc. 1st Int. Workshop, Menlo Park, Calif., Feb. 1986. New York, 1986.– c. 326-341
Yao S.B. Approximating Block Acess in Database Organizations // Commun. ACM.– 1977.– 20, N 4.– c. 260-261
Lohman G.M., Daniels D., Haas L.M., Kistler R., Selinger P.G. Optimization of Nested Queries in a Distributed Relational Database // Proc. 10th Int. Conf. Very Large Data Bases, Singapore, Aug. 27-31, 1984. New York, 1984.
Методы оптимизации запросов в реляционных системах [електронний ресурс]. – Режим доступу: http://www.sdteam.com/t1951
Оптимизация запросов в системах баз данных [електронний ресурс]. – Режим доступу: http://citforum.ru/.../query_optimization/
Методы оптимизации выполнения запросов в реляционных СУБД [електронний ресурс]. – Режим доступу: http://citforum.ru/.../art_26.shtml
Eddies: Continuously Adaptive Query Processing [електронний ресурс]. – Режим доступу: http://db.cs.berkeley.edu/papers/sigmod00-eddy.pdf
Динамическая оптимизация распределения данных по узлам сети [електронний ресурс]. – Режим доступу: http://masters.donntu.ru/.../index.htm
Динамическая оптимизация распределения данных по узлам вычислительной сети [електронний ресурс]. – Режим доступу: http://masters.donntu.ru/.../index.htm
Исследование свойств распределенных систем обработки данных [електронний ресурс]. – Режим доступу: http://masters.donntu.ru/.../index.htm
Разработка графо-аналитической модели учета нагрузок веб-базированных систем [електронний ресурс]. – Режим доступу: http://masters.donntu.ru/.../article2.htm