Прогнозирование курса биржевых котировок на основе статистических данных финансового рынка с использованием современных методов моделирования

Введение

Существование в рамках современной экономической системы обусловлено множественными рисками. Колебания валютных курсов, изменение спроса и предложения в тех или иных областях, различные внутренние и внешние факторы экономико-политического характера безусловно влияют как на всю систему в целом, так и на отдельные её составляющие на всех уровнях. Необходимость формирования стратегии действий в условиях подобного рода неопределённости безусловно актуализирует задачу моделирования данных процессов для всех участников рынка – от государств, для которых динамика и предсказуемость изменения курса национальной валюты определяет уровень доверия населения и предпринимателей к правительству страны, до непосредственно предпринимателей разного уровня и физических лиц, для которых динамика курсов валют определяет вектор инвестиций и рыночные стратегии.

При этом, достоверность и долговечность разрабатываемых моделей выходит на первый план в рамках задачи планирования – чем точнее прогнозы модели, чем более долгосрочный прогноз она возвращает, тем более детализированную стратегию может формировать тот или иной участник рынка.

Цель и задачи исследования, планируемые результаты

Целью данного исследования является определение инструментальной области и формирование вектора развития дальнейших исследований в области разработки методов, способных повысить предсказательную точность моделей, используемых при анализе поведения рынка.

1. Основные понятия и определения

Используемые методы и приемы прогнозирования в контексте финансов можно классифицировать по следующим параметрам[1]:

• По признаку оценки: на качественные (как правило — это экспертные оценки, основанные на суждениях и умозаключениях) и количественные (основанные на расчёте числовых показателей)
• По информационной составляющей: на статические (формализованные) и интуитивные.

Таким образом, учитывая требования к универсальности методов в рамках задачи прогнозирования поведения системы, объектом данного исследования в основном будут как раз количественные формализованные методы, основным источником информации для которых будет служить история цены актива, представленная в виде временных рядов.

1.1. Временной ряд

Временные ряды (ряды динамики) – это наборы изменяющихся во времени значений некоторого показателя, сгруппированные в хронологическом порядке [2]. Как правило они представляют собой последовательные наборы значений $y_{1},y_{2},...,y_{n}$, называемыми так же уровнями ряда, каждый из уровней имеет в соответствии некоторый момент времени $t_{1},t_{2},...,t_{n}$

Классификация временных рядов весьма разнообразна. Их разделяют по множеству признаков [2], например:

• По форме представления уровней: на ряды абсолютных и средних показателей, ряды средних величин;
• По характеру временного ряда: на моментные и интервальные;
• По временному расстоянию между уровнями ряда: на равноотстоящие и неравноотстоящие;

В данном контексте наиболее весомым параметром классификации является характер случайного процесса, разделяющее ряды на стационарные и нестационарные.

1.2. Стационарность

Случайный процесс является строго стационарным (стационарным в узком смысле), если его конечномерные распределения инвариантны относительно сдвига по времени, т.е. если его многомерная плотность вероятности произвольной размерности $n$ не изменяется при одновременном сдвиге всех временных отрезков $t_{1},t_{2},...,t_{n}$ на одинаковую величину $\tau$[3][4]:

Данный фактор во многом определяет какие методы будут использоваться во время анализа временного ряда. Это связано с тем, что большинство алгоритмов, на основе которых строятся различные статистические критерии, спектральные и корреляционные методы всегда отталкиваются от постоянства математического ожидания и дисперсии, что как раз и является следствием стационарности [3]. Более того, т. к. данное свойство является определяющим в контексте временных рядов, именно его и указывают во многих источниках в качестве определения стационарности, расширяя таким образом введённое понятие. Таким образом в широком смысле определение стационарности звучит следующим образом: случайный процесс $x(t)$ называется стационарным, если его математическое ожидание и дисперсия постоянны во времени, а автоковариационная функция зависит лишь от разности аргументов [4]:

Важным замечанием здесь будет то, что на практике чисто теоретическое определение стационарности случайного процесса не применимо. Гипотеза о стационарности исходного временного ряда проверяется с помощью некоторых статистических критериев, позволяющих оценить с некоторой доверительной вероятностью оценить, насколько характеристики временного ряда удовлетворяют критерию стационарности (например KPSS-test).

На практике, временные ряды редко когда оказываются стационарными, в то время как стационарные ряды изучены намного лучше. Поведение таких рядов более предсказуемо, поэтому легче поддаётся анализу и, что самое важное прогнозу [3], поэтому, если есть такая возможность, выполняются процедура сведения к стационарности, первым и важнейшим этапом которой является выделение трендовой составляющей [6], после чего, в т.ч. с помощью методов спектрального анализа, выделяют оставшиеся детерминированные компоненты модели временного ряда – циклическую и сезонную.

1.3. Модели временных рядов

В основе всех временных рядов лежит случайный процесс, охарактеризовать который можно различными способами: описав некоторые его статистические характеристики, такие как функция распределения или же построив его некоторую характеристическую модель [7].

Вариантов моделей, моделирующих такие процессы существует весьма обширное количество. Одной из наиболее часто встречающихся моделей является так называемая аддитивная модель, характеризующая процесс как сумму некоторой детерминированной ($q$) и случайной ($\xi$) составляющей, которую так же часто называют шумом:

Наряду с аддитивными моделями, очевидно, существуют и мультипликативные, а также смешанные модели в которых одновременно присутствует как аддитивная, так и мультипликативная составляющие:

Кроме того, для стационарных временных рядов, существует ряд моделей, описывающих их через математическое отношение между последующими и предыдущими значениями временного ряда, а также, в некоторых случаях, их шумами. Такие модели называются авторегрессионными и могут быть сведены к следующей формуле:

1.4. Тренд, цикл и сезонность

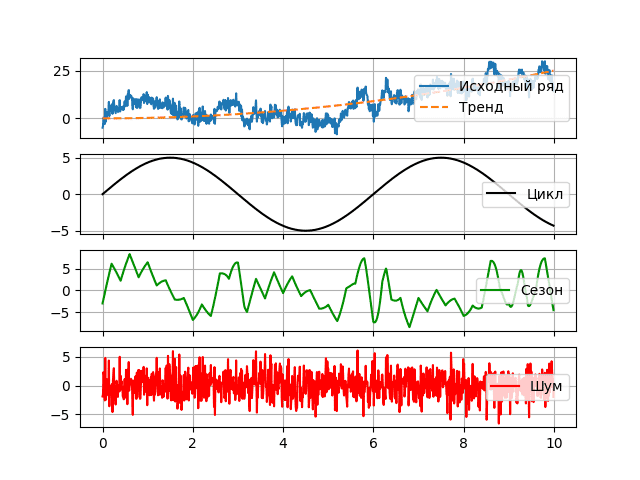
Детерминированная составляющая временного ряда $q$ может быть любой, сколь угодно сложной математической функцией. От способа её разбиения зависит подкласс модели, однако в общем случае, все модели так или иначе оперируют следующими компонентами: трендовой, сезонной и циклической:

Тренд ($\tau$) представляет собой некоторую общую тенденцию, наблюдаемую в течение длительного периода времени. Обычно описывается простой монотонной функцией от времени [8].

Наличие сезонной компоненты ($s$) связывается с наличием в случайном процессе факторов, влияние которых определяется некоторой периодичностью (день недели, месяц, год). Как правило она связана с некоторыми факторами, происходящими в рекальной жизни – такими как выходные дни, праздники, время сбора урожая, время отпусков и пр. Особым свойством сезонной компоненты является возможность её плавающий характер – возможность изменения с течением времени, поэтому их называют квазипериодическими [7].

Цклическая (периодическая) компонента ($p$) представляет собой некоторую неслучайную функцию с ярко выраженной тригонометрической составляющей, определяющую длительные периоды смены циклов [9].

При анализе временных рядов, сезонными называют квазипериодические компоненты высокой частоты, в то время как циклами являются гораздо более устойчивые к изменениям более долгосрочные компоненты. При этом в рамках одной модели может существовать несколько сезонных и циклических компонент, а взаимосвязь может быть описана различными отношениями. Таким образом, например, общий вид аддитивных может быть представлен в виде следующего выражения:

где $\omega_\tau, \omega_s, \omega_p$ – коэффициенты наличия или отсутствия, принимающие исключительно значения 1 и 0.

1.5. Точка бифуркации

При анализе и вычислении трендовой составляющей важно помнить о том, что система, порождающая случайный процесс может быть подвержена влиянию различных внутренних и внешних факторов, в следствие которого характер его тренда может значительно изменяться.

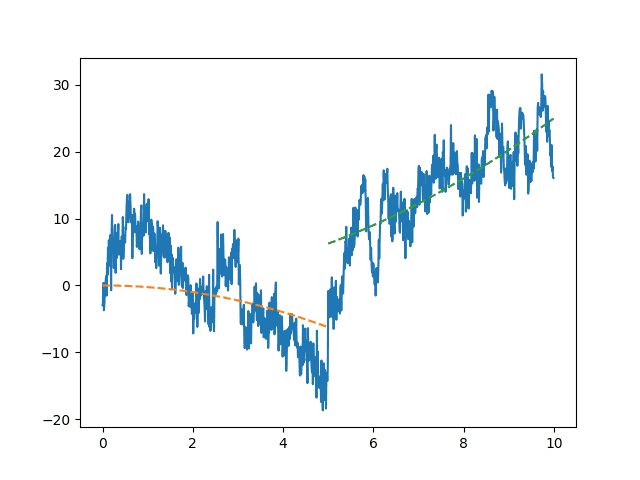
В то же время, методы экстраполяции с достаточной точностью могут описывать поведение в рамках одного процесса, однако в то же время они не годятся в момент их смены [10]. Таким образом, одним из этапов исследования временного ряда является поиск так называемых точек бифуркации - моментов времени в исследуемом ряде, соответствующих резкому изменению поведения системы. В интервалах же между точками бифуркации системы, её поведение предсказуемо и стабильно, определяемо с помощью вышеописанных факторов.

1.6. Спектральный анализ

После выделения трендовой составляющей детерминированной части ряда, возникает необходимость определения различных периодических и квазипериодических его компонент и в этом случае серьёзным подспорьем могут стать методы спектрального анализа [11], позволяющие выявить скрытые циклические паттерны во временных рядах. При этом многие модели временных рядов (Сезонная декомпозиция, SARIMA) в той или иной степени предполагают, что исследователю известны некоторые параметры частотных характеристик ряда, что делает методы спектрального анализа мощным инструментом при обработке временных рядов.

Методов спектрального анализа существует достаточно много и все они основываются на одной идее – они переводят данные из плоскости значение/время в плоскость амплитуда/частота, выводя на передний план тем самым частотные характеристики ряда.

1.7. Нейросетевое моделирование

Отдельного упоминания в контексте моделирования временных рядов достойны технологии нейросетей. Важным аспектом этих алгоритмов является их способность к обобщению – нейронные сети в процессе обучения способны находить нетривиальные связи внутри данных, а значит и повышать предсказательную способность модели.

Рекуррентные нейронные сети. Этот вид алгоритмов хорошо подходит для обработки последовательностей [12]. Основная идея таких нейросетей, в отличие от перцептрона, заключается в том, что выход нейросети на очередном элементе последовательности зависит от предыдущих результатов.

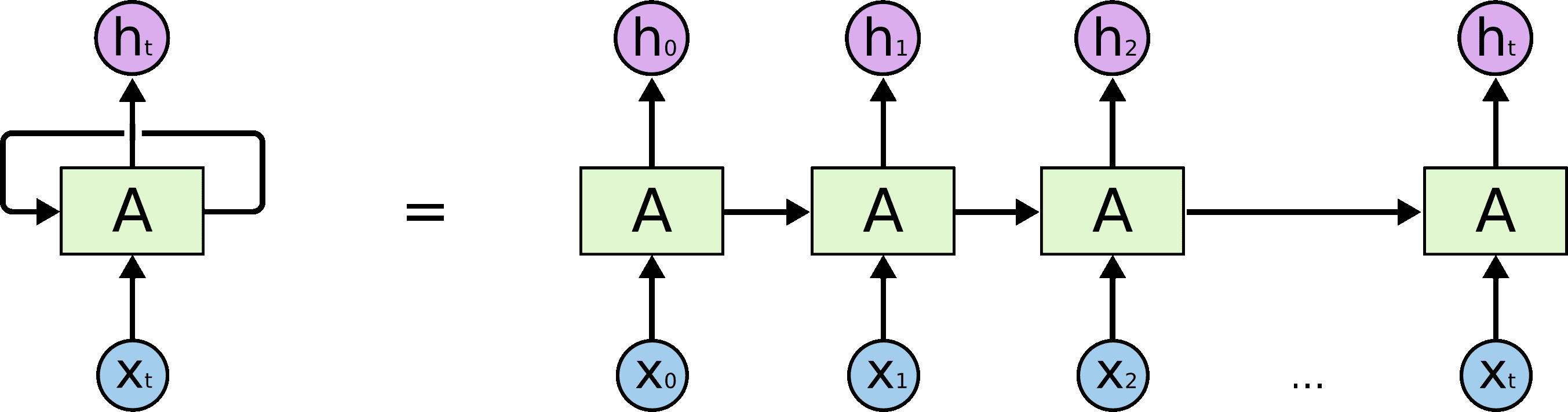
Вследствие своей структуры, можно сказать, что рекуррентные нейронные сети в общем смысле являются представителями авторегрессионных моделей, т.к. они отображают взаимосвязь между разнесёнными во времени уровнями временного ряда.

Однако у рекуррентных нейронных сетей всё же существует ряд недостатков: проблема взрыва и затухания градиента и проблема распараллеливания. В силу того, что в процессе вычислений возникает многократное повторение умножений на одно и то же значение весов, градиенты либо стремиться к бесконечности, либо к нулю, что делает получение информации от далёких по времени состояний затруднительным [13]. Данную проблему решают с помощью внесения определённых изменений в структуру модели. Однако проблема распараллеливания возникает как следствие самой архитектуры нейросети: распараллелить вычисления нельзя, поскольку каждое следующее внутреннее состояние системы зависит от предыдущего.

Отказываясь от рекуррентной модели данные проблемы решают нейросети-трансформеры, основной идей которых стало то, что токены проходят через слои параллельно друг с другом, взаимодействуя с помощью внутреннего слоя Multi-head attention. Это специальный слой, позволяющий каждому входному токену взаимодействовать с другими с помощью механизма внимания [15].

На вход этого слоя подаются вектора $Query$ и некоторое количество пар $(Key, Value)$. Каждый из них преобразуется линейным преобразованием, после чего вычисляется скалярное произведение $Query$ со всеми $Key$ по очереди, обрабатывается с помощью логистической функции и суммируются в единый вектор с $value$. Его отличие от раннее встречавшихся в других работах attention-ов заключается в том, что таких слоёв параллельно тренируется несколько (на рисунке – $h$). После чего результат ещё раз конкатенируется, обрабатывается с помощью обучаемого линейного преобразования и возвращается.

С точки зрения прогноза временных рядов, такой многослойный механизм позволяет обрабатывать последовательность с разных аспектов – случайное заполнение начальных весов вполне достаточно для того, чтобы направить поиск закономерностей по разным путям. Кроме того, подобный механизм позволяет проектировать мультимодальные системы, способные на одновременную обработку разных типов данных.

2. Обоснование направления дальнейшей разработки

Таким образом, для увеличения точности моделирования финансовых процессов, необходимо подходить к проблеме комплексно, увеличивая точность на всех этапах анализа и моделирования временных рядов.

2.1. Поиск точек бифуркации

Т.к. в точках бифуркации поведение системы изменяется непредсказуемым образом, необходимо исключение их влияния на анализируемый ряд, путём исключения соответствующих трендовых составляющих. Однако, во многих случаях визуальный анализ не позволяет однозначно указать на наличие таких точек в ряде. Отсюда возникает необходимость в определённом алгоритме, позволяющем с высокой достоверностью находить моменты смены процессов, которым подчиняется поведение ряда, а также способном подтверждать наличие этих точек.

Алгоритм поиска точек бифуркации, основан на замене отрезков временного ряда математической моделью и сравнении моделей этих моделей. При этом в качестве тренда выступать любая модель, детерминированная для исходных и прогнозируемых значений времени [10].

Так как предполагается, что найденная точка бифуркации делит ряд на два независимых отрезка, можно утверждать, что для нахождения оптимального тренда для прогноза, дальнейший поиск мест слома тренда необходимо и достаточно проводить в области, лежащей справа на временной шкале относительно точки бифуркации.

Таким образом, алгоритм поиска точек бифуркации временного ряда можно описать следующим образом. Предположим, имеется временной ряд $y(x):(x_i, y_i), i=0,1,2,...N$, а также предполагаемая модель $f(x)$, имеющая $k$ степеней свободы. В таком случае, для каждого $n_1\in[k-1;N-(k-1)]$ необходимо рассчитать:

Получив, в итоге, $2k-1$ потенциальных точек бифуркации и по две модели ряда для каждой из них, оценив которые с помощью метрики расстояния, можно определить, какая из моделей подходит наилучшим образом, минимизируя найденные расстояния. Например:

В данном случае в качестве метрики использовался квадрат расстояния, однако, следует упомянуть, что он не является универсально лучшим, список метрик довольно разнообразный [16][17]. Найденное таким образом значение $n_1$ будет соответствовать точке бифуркации временного ряда при использовании модели $f$ на указанном промежутке.

Далее, с помощью статистических тестов (например F-критерия Фишера), необходимо определить статистическую значимость полученного разбиения, сравнив отношение дисперсии всего $\sigma_{\mbox{ряда}}$ ряда и суммарной дисперсии двух его отрезков $ \sigma_{\mbox{ступ}} $ с критическим значением $F_{\mbox{кр}}$

Выполнение неравенства (14) в данном случае определяет статистическую значимость разбиения с заданной при определении $F_{\mbox{кр}}$ доверительной вероятностью $\alpha$ – в этом случае, процесс поиска точки бифуркации повторяется для $i \in \lbrack n_1;M \rbrack $, в противном – за модель всего ряда полагается $ \overline{y}=f(x_i), i \in \lbrack 1;N \rbrack $ и алгоритм завершает свою работу.

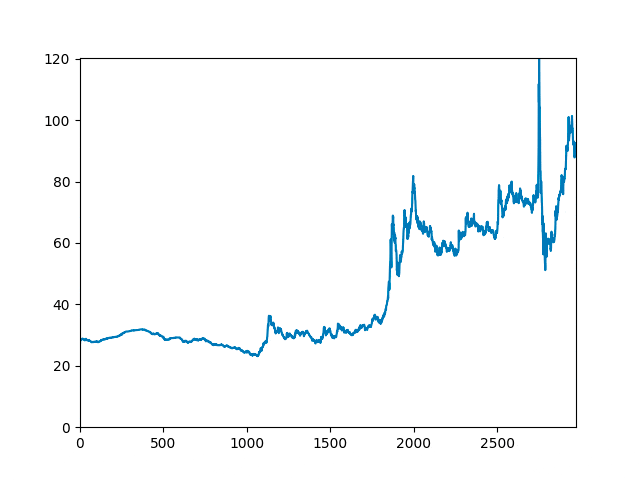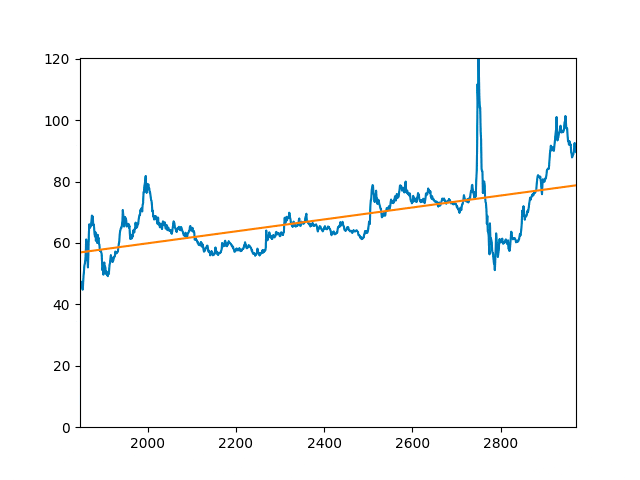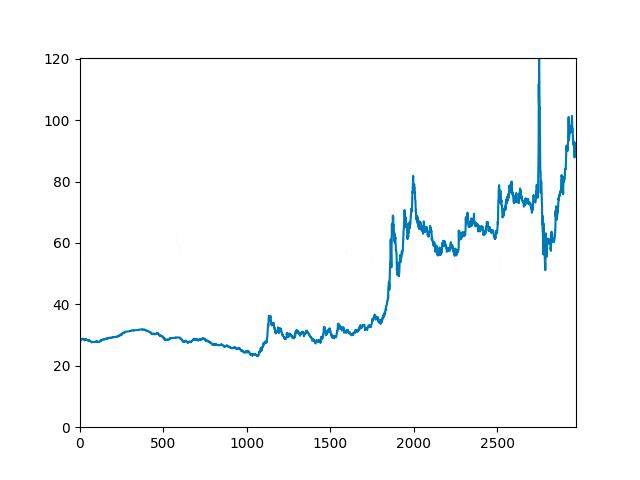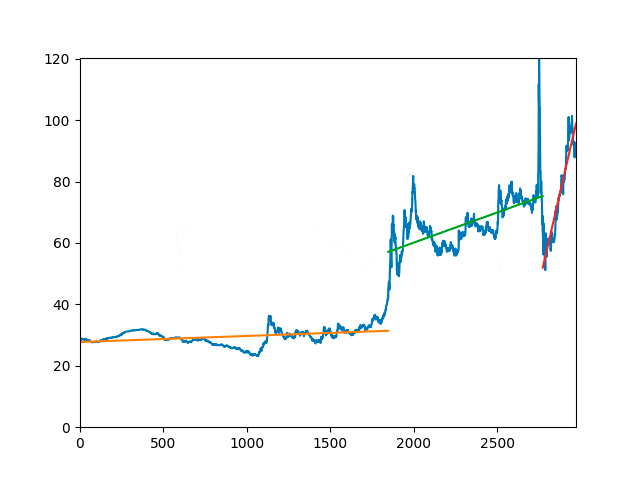
2.2. Спектральный анализ

Спектральный анализ представляет собой один из наиболее эффективных методов выявления причинных связей между компонентами изучаемых процессов. Применяя принципы спектрального разложения измеряемых функций на индивидуальные спектральные компоненты, можно выделить значимую информацию даже в условиях влияния помех [18]. Базируясь на идее разложения функции в некотором частотном диапазоне, данная группа методов способна помочь исследователям с достаточно большой точностью оценить периодическую и сезонную составляющие модели временного ряда.

Стоит отметить, что, несмотря на широкое множество инструментов спектрального анализа, основной фокус данного раздела направлен на одну конкретную группу методов, а именно – вейвлет-преобразование. Это связано с их общей универсальностью: данный вид преобразований реализует компромиссное решение между разрешением во временном и частотном спектрах. Кроме того, вейвлет преобразование разворачивает ряд в трёхмерном пространстве амплитуда/время/частота, что позволяет чётко выделять локализованные во времени временные составляющие, а возможность обратного синтеза ряда позволяет производить преобразования над данными на этапе разложения.

Таким образом можно определить три направления применимости спектральных преобразований при моделировании поведения временного ряда: визуальный анализ спектральной компоненты, использование шумоподавления для подготовки данных и моделирование разложений.

2.2.1. Визуальное выделение частотных компонент ряда

По сути своей, это направление – прямое применение вейвлет-анализа к временному ряду. Построив скейлограмму ряда с помощью непрерывного вейвлет-преобразования, становится возможной визуальная оценка периодических компонент:

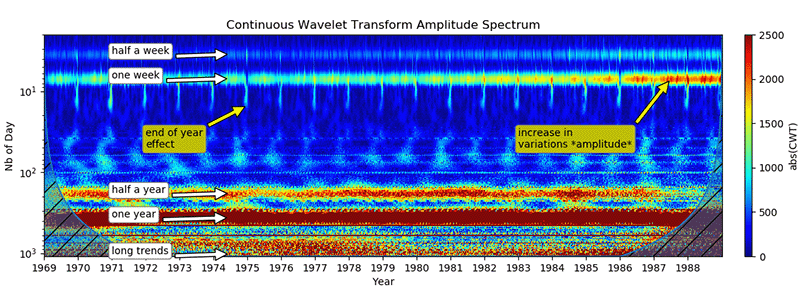
Непрерывное вейвлет преобразование, разворачивая ряд пространстве амплитуда/частота/время, позволяет визуально оценить частотные составляющие, время их появления и исчезновения, что позволяет их примерно описать, сформировав некоторую модель, которая в дальнейшем может быть уточнена с помощью различных методов фиттинга.

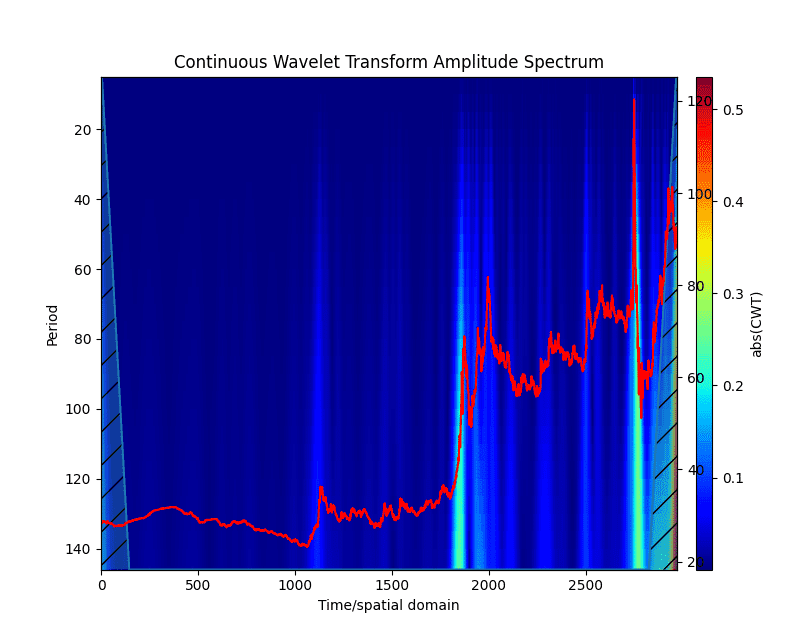
В дополнение к методу, описанному в предшествующем разделе, точки бифуркации ряда будут достаточно чётко видны на скейлограмме – в моменты смены тренда на ней будет видны чётко выраженные пики, затрагивающие если не все, то большинство частот (рис. 7).

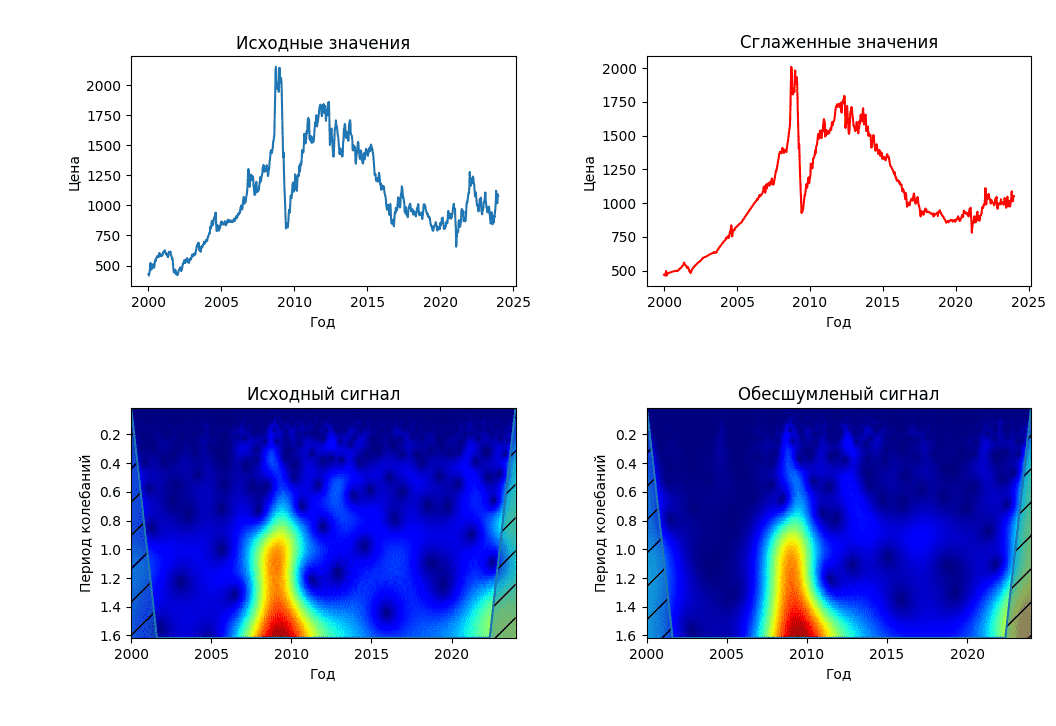
2.2.2. Использование шумоподавления

Для большинства сигналов их низкочастотная составляющая является наиболее важной частью потому, что с ее помощью можно идентифицировать сигнал. Высокочастотная составляющая в свою очередь несет в себе очертания сигнала. Если в сигнале её удалить, то он поменяется, но основное его поведение останется распознаваемым. Однако если удалить большое количество низкочастотных компонент сигнала, он станет нераспознаваемым. В вейвлет-анализе приближения исследуются на больших масштабах, низкочастотные составляющие и детализации – на маленьких.

Для шумопонижения в данном методе используется трешолдинг [19] (пороговая обработка данных) – техника исследования сигналов, содержащих шум, осуществляющая декомпозицию исходного сигнала в вейвлет-спектр, который в дальнейшем подвергается обработке.

Выбирается некоторое значение коэффициента фильтрации $k$, определяющее степень сглаживания значений и соответствующая ему степень трешолдинга $\Delta$, как правило рассчитывающаяся по формуле:

где $Y_{max}$ – наибольшее значение амплитуды в спектре.

Таким образом, значения меньше $\Delta$ в спектре заменяются на 0, а выше или равные ему – ужимаются в направлении 0 на $\Delta$. При жёстком трешолдинге, значения меньше $\Delta$ заменяются на 0, а большие значения при этом остаются неизменными.

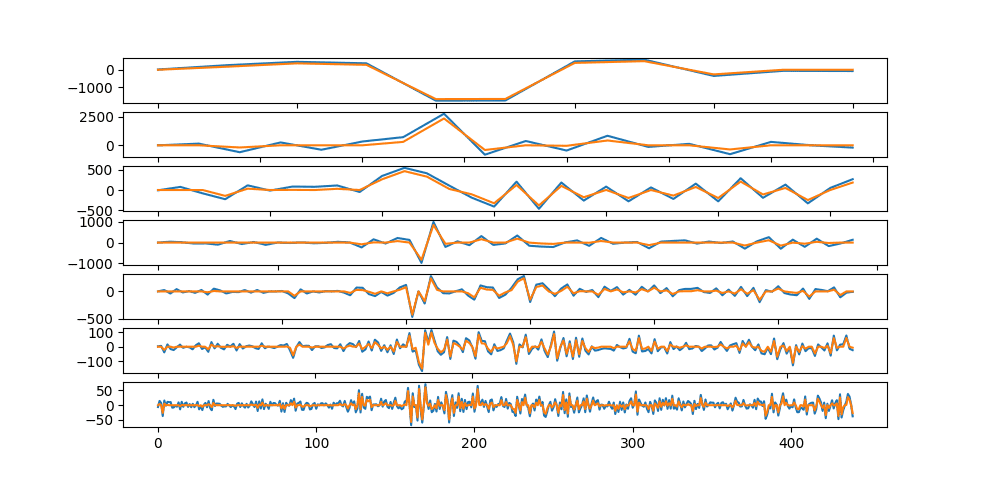
После чего исходный сигнал синтезируется обратно:

2.2.3. Синтез новых значений ряда с помощью разложений

Как уже было сказано раннее, результатом работы вейвлет-преобразования является некоторое количество последовательностей, упорядоченных во времени. Данные последовательности, в свою очередь, отражают процессы, происходящие внутри систем, порождающих ряд, разложенные на некотором спектре частот (Рис. 6), при этом значения этих последовательностей сохраняют сохранять упорядоченность во времени. Следовательно, представляется возможность анализировать их как отдельные временные ряды с последующим моделированием и предсказанием новых значений в каждом частотном спектре отдельно. При этом, синтезировав ряд с учётом новыми значениями, можно получить прогноз.

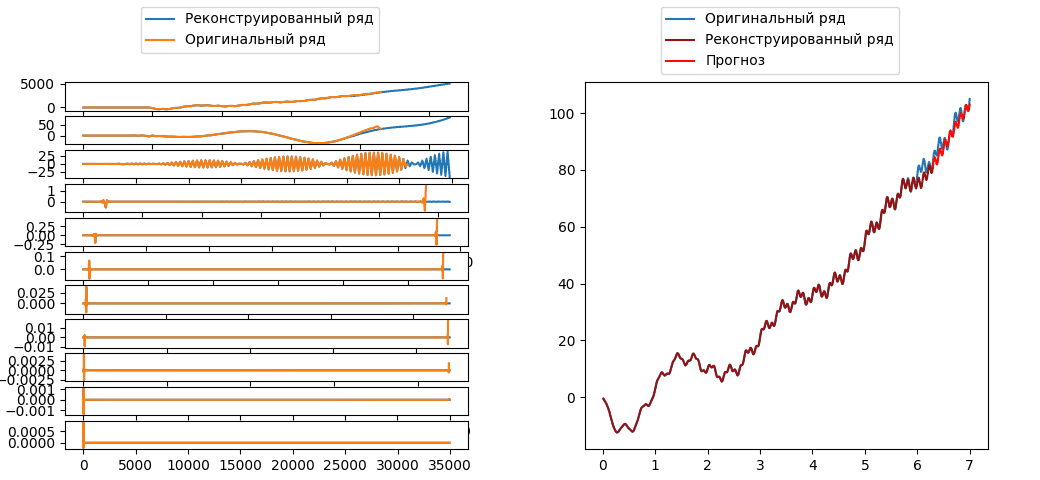
Допустим на вход алгоритма дискретного вейвлет-преобразования поступает последовательность чисел длинны $N$. Один этап такого разложения вычленяет две составляющие – низкочастотную и высокочастотную. Данные наборы значений также называют коэффициентами аппроксимации ($cA$) и детализации ($cD$). Таким образом, если длина фильтра преобразования равна L, то длина результирующих последовательностей будет равняться:

Следовательно, таким образом, для прогнозирования $\Delta$ следующих значений оригинального ряда, необходимо сформировать $\DeltaN_{cA}=\DeltaN_{cD}$ новых значений искомых последовательностей:

На следующем этапе, за исходную последовательность принимают уже набор коэффициентов аппроксимации и алгоритм повторяется. Следовательно, если $i$ – номер итерации цикла, то из (7) и (8) следует:

Так как временные ряды представляют собой некоторые конечные числовые последовательности, при декомпозиции возникает необходимость их экстраполяции. Это неизбежно влияет на структуру данных у границ последовательностей [20], в той или иной степени искажая результаты. Данный эффект хорошо изучен и называется краевым эффектом. При классическом применении вейвлет-анализа данный эффект необходимо лишь иметь ввиду при работе с периодограммой, существует множество способов экстраполяции сигнала [21] и степень доверия к таким данным определяется исследователем. При восстановлении де исходного ряда эффект и вовсе нивелируется. В случае же применения этого метода в ключе, описанном в данном разделе, влияние данного эффекта может сказаться на выстроенной модели.

Допустим в качестве исходного ряда выступает следующая последовательность:

В таком случае, результатами работы алгоритма являются последовательности коэффициентов:

Так как в процессе расчётов вейвлет как-бы «скользит» вдоль исходного ряда, то при длине фильтра $L$, для вычисления $cA_i$ и $cD_i$ используется следующий диапазон значений $y$:

Следовательно, краевые эффекты возникают на границах значений в пределах $\gamma=\lfloor\frac{L}{2}\rfloor$ элементов от края.

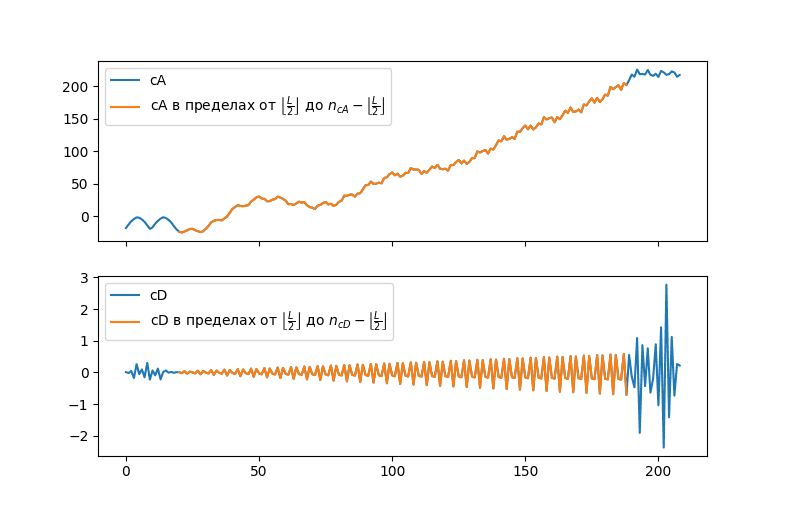
При этом, чем ближе к границе, тем больше экстраполированных значений и тем меньше реальных значений ряда будет использовано при расчётах. А следовательно, тем более сильным будет влияние искажающих факторов. В то же время, находящиеся в этих пределах значения ряда несут в себе полезную информацию, которая сильнее всего будет влиять на данные точек в пределах $\gamma$ значений от края. Следовательно, при построении моделей необходимо искать компромисс между двумя позициями: отказ от использования значений, находящихся в пределах γ от границ будет значить потерю данных, находящихся в этих точках при формировании модели ряда, в то же время, использование этих точек будет неизбежно искажать результаты модели.

2.3. Информационный контекст

Несмотря на все их достоинства, проблема вышеописанных подходов заключается в том, что они исследуют временной ряд как исключительную абстракцию, «в отрыве от внешнего мира». Это значит, что предсказать, к примеру, положение новой точки бифуркации в ряде не представляется возможным.

Обычная практика в таком случае – использование метода экспертных оценок. Проанализировав поведение системы с помощью некоторого пула экспертов, можно с определённой долей вероятности предсказать её поведение. Однако, стоит учитывать, что в таком случае, полученный результат будет содержать в себе изрядную долю субъективности, что так или иначе может повлиять на точность прогноза.

С другой же стороны, существует огромное множество интернет-ресурсов и площадок, на которых публикуются различные анонсы, новости и заявления. Известны случаи, когда высказывания публичных спикеров становились причинами изменений на фондовом рынке. Это можно назвать информационным контекстом финансовых временных рядов.

Сформировав на основе истории цен тех или иных активов и соответствующих им новостных постов, обучающую выборку, возможно попытаться обучить модель, предсказывающую поведение системы.

По аналогии с алгоритмами генерации изображений [22], на вход такой модели должен попадать некоторый набор числовых последовательностей, представляющих собой набор цен того или иного актива за определённый период, и текстовый промпт, являющийся, в данном случае, набором новостных статей по заданному активу, первичный анализ которого возможно возложить на уже существующие в открытом доступе NLP модели. Полученные таким образом наборы токенов будут, наряду с наборами параметров, на вход внутренних слоёв, результатом работы которых будет некоторая оценка семантической близости полученных на входе наборов данных.

Таким образом данный алгоритм должен исполнять роль эксперта в данной области, оценивая, насколько текущие параметры и внешний вид моделей соответствует информационному контексту.

Выводы

Исследование временных рядов требует в основе своей комплексного подхода и одновременного применения различных методик, позволяющих выделить ту или иную составляющую временного ряда. Рассмотренные методы исследования финансовых временных рядов представляют собой эффективные подходы к анализу и моделированию динамических процессов. Однако, основная их проблема, как и большинства других, заключается в работе с временными рядами как абстракциями, без учёта влияния внешних факторов. Это накладывает определённые требования на сам ряд, а так же безусловно ограничивает прогностическую способность исследователя. Подход с использованием экспертных оценок, хоть и способен принимать во внимание внешний информационный контекст, но при этом уязвим для когнитивных искажений и субъективных ошибок самих экспертов.

Следовательно, одним из перспективных направлений дальнейших исследований, может быть, интеграция информационного контекста в анализ финансовых временных рядов. Введение новостных статей, анонсов и заявлений как дополнительных параметров анализа позволит учесть внешние факторы, которые могут оказывать влияние на общую динамику рынка. Это создаст более реалистичные и прогностически ценные модели, способные учесть не только внутренние процессы, но и реакции рынка на внешние события. Параллельно с этим, дальнейшие исследования могут и должны быть направлены на разработку и совершенствование уже существующих методов анализа и моделирования рядов динамики.

Список использованных источников

1. Бизнес-прогнозирование: какой метод выбрать. / В. Клавдеева – Управление предприятием – 2023
2. Теория статистики: Учебно-методический комплекс. / В.Г. Минашкин, Р.А. Шмойлова, Н.А. Садовникова, Л.Г. Моисейкина, Е.С. Рыбакова – М.: Изд. центр ЕАОИ. – 2008.
3. Методы анализа и прогнозирования временных рядов / С. В.Поршнев, Н. Т.Сафиуллин – УрФУ - 2022
4. Краткий курс теории случайных процессов. [Электронный курс] / М.К. Ризаева, Т.Ю Гаджиева - Дагестанский Государственный университет - 2018 - Режим доступа: [ссылка]
5. Анализ времененных рядов. [Электронный ресурс] / А.Михайлов - 2023 - Режим доступа:[ссылка]
6. Методы анализа временных рядов [Электронный ресурс] / Н.А. Хованова, И.А. Хованов - 2001 - Режим доступа:[ссылка]
7. Анализ временных рядов и прогнозирование. / Н.А. Садовникова Р.А. Шмойлова – М.: «Футурис» – 2009
8. Телятников З. Анализ временных рядов. / З.Телятников - k-tree - 2023
9. Методы анализа временных рядов / Т.В. Саженкова, И.В. Пономарѐв, С.П. Пронь – Барнаул: Издво Алт. ун-та. – 2020
10. Алгоритм поиска момента смены тренда во временных рядах метеорологических величин / А.Д. Кузнецов, А.Г. Саенко, О.С. Сероухова, Т.Е. Симакина - Вестник ТвГУ. Серия: Прикладная математика - 2019
11. Спектрально-кореляционный анализ равномерных рядов / В.В. Витязев - Изд-во С.Петербю ун-та - 2001
12. Understanding LSTM Network. [Электронный курс] / Б. Рохрер - 2015 - Режим доступа: [ссылка]
13. Нейросети для работы с последовательностями / А. Янина - Учебник по машинному обучению - 2023
14. Рекуррентные нейронные сети [Электронный курс] / В.Кустивкова - Приволжский научно-образовательный цент суперкомпьютерных технологий - 2018 - Режим доступа: [ссылка]
15. Attention Is all you need. [Электронный курс] / A.Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. Gomez, L. Kaiser, I. Polosukhin - 2023 - Режим доступа: [ссылка]
16. Оценка возможностей метода аналогов для текущего прогноза температуры воздуха / Восканян К.Л., Кузнецов А.Д., Сероухова О.С., Симакина Т.Е. - Вестник ТвГУ. - Серия: Прикладная математика. - 2019.
17. Текущее прогнозирование экологических измерений на основе поиска аналогов / Восканян К.Л., Кузнецов А.Д., Сероухова О.С., Симакина Т.Е. - Сборник тезисов XI научно-прикладной международной конференции «Естественные и антропогенные аэрозоли» - 2018 г.
18. Применение спектрального анализа при обработке геофмизческих данных / А.И. Банщиков, Б.А. Спасский - Вестник Пермского Университета - 2011
19. PyWavelets: A Python package for wavelet analysis / Gregory R. Lee, Ralf Gommers, Filip Wasilewski, Kai Wohlfahrt, Aaron O’Leary – Journal of Open Source Software – 2019
20. Анализ способов устранения краевого эффекта при спектральном анализе сигналов методом вейвлет-преобразования / Киселёв Б.Ю. – Международный журнал прикладных и фундаментальных исследований № 10 – 2017
21. Statistics and Machine Learning Toolbox Documentatio [Электронный ресурс] / The MathWorks Inc. – 2023 – Режим доступа: [ссылка]
22. Как работают нейронные генераторы картинок [Электронный ресурс] / А.Капранов - 2022 - Режим доступа: [ссылка]