Мищук Юлия Константиновна
Факультет:
Компьютерных наук и технологий
Специальность:
Программное обеспечение автоматизированных систем
Тема магистрской диссертации:
Анализ эффективности вычислительных систем с использованием Марковской модели
Руководитель:
Фельдман Лев Петрович
Реферат по теме выпускной работы:
«Анализ эффективности вычислительных систем с использованием марковской модели»
Цели и задачи
- Обзор и анализ современных вычислительных систем.
- Обзор и анализ методов анализа вычислительных систем.
- Разработать модель однородного кластера с совместным использованием дискового пространства
- Программно реализовать модель на параллельных системах.
- Оценить эффективность реализации.
Актуальность
В связи с необходимостью увеличения вычисляемых мощностей во многих сферах жизнедеятельности человека, активно разрабатываются алгоритмы улучшения работы вычислительных систем – систем обработки данных, настроенных на решение задач, конкретной области применения. Основополагающими в теории вычислительных систем являются модели и аппарат теории марковских процессов.
Понятие архитектуры высокопроизводительной системы является достаточно широким, поскольку под архитектурой можно понимать и способ параллельной обработки данных, используемый в системе, и организацию памяти, и топологию связи между процессорами, и способ исполнения системой арифметических операций. Рассматривается кластерная архитектура многопроцессорных вычислительных систем [1]. Учитывая трудоёмкость и большие объемы данных, марковские модели не использовались в больших системах, поэтому задача является актуальной [2]. В данной работе необходимо проанализировать эффективность распараллеливания метода и выяснить, насколько ускорилось моделирование многопроцессорной системы [3].
Научная значимость
Создание и использование современных суперкомпьютерных систем стало в наше время одним из основных направлений в ведущих странах мира. Одной из основных проблем, возникающих при проектировании и эксплуатации параллельных и распределенных вычислительных систем (ВС) является выработка рекомендаций рационального использования ресурсов вычислительной среды. Одним из эффективных способов решения этой проблемы может быть использование рзультатов непрерывных или дискретных аналитических моделей [4].
Обзор исследований и разработок по теме
Существует целый ряд отраслей (таких, как: науки о Земле (физика атмосферы, метеорология, климатология, физика океана); математическая лингвистика (распознавание речи, анализ текста); биология, экология; экономика; социальные науки; информатика (распределенные вычислительные системы, распознавание образов, ведение БД) ; медицина; фармацевтика и т.д.), в которых возникает необходимость решения больших объемов вычислений за приемлемое счетное время [5].
Рост вычислительной мощности компьютерных систем, появление современных суперкомпьютеров, кластеров рабочих станций, постоянное повышение мощности компьютерных систем приводит к тому, что задачи, которые еще в недалеком прошлом не могли быть решены в реальном масштабе времени, успешно решаются благодаря использованию параллельных алгоритмов, реализуется на многопроцессорных системах, обладающих высоким быстродействием.
В связи с этим, активно разрабатываются алгоритмы улучшения работы вычислительных систем. Работы в этом направлении не теряют своей актуальности и требуют дальнейшего развития, нахождения новых решений.
В ДонНТУ над этими вопросами работают:
- Доктор технических наук, профессор, Фельдман Лев Петрович,
- Кандидат технических наук, доцент Михайлова Татьяна Васильевна,
- Кандидат технических наук, доцент Ладыженский Юрий Валентинович
так же в последние годы подобной тематикой занимались магистранты:
Дяченко Татьяна Федоровна (Руководитель: к.физ-мат.н., доцент Дацун Наталья Николаевна)
Тема магистерской работы: «Исследование параллельного алгоритма построения Марковских моделей вычислительных систем»Кучереносова Ольга Владимировна (Руководитель: д.т.н., профессор Башков Евгений Александрович)
Тема магистерской работы: «Исследование эффективности параллельных вычислительных систем»Алтынпара Евгений Олегович (Руководитель: к.т.н., доцент Ладыженский Юрий Валентинович)
Тема магистерской работы: «Решение задач большой размерности на кластере»Морозов Роман Николаевич (Руководитель: к.т.н., доцент Ладыженский Юрий Валентинович)
Тема магистерской работы: «Распределенные алгоритмы решения задач высокой размерности на вычислительном кластере»Завалкин Дмитрий Александрович (Руководитель: д.т.н., профессор Фельдман Лев Петрович)
Тема магистерской работы: «Анализ и оценка эффективности параллельных разностных методов решения ОДУ на кластере»Аль-Масри Мохаммед Рида (Руководитель: к.т.н., доцент Ладыженский Юрий Валентинович)
Тема магистерской работы: «Параллельные методы решения систем линейных алгебраических уравнений на вычислительном кластере»
Общие понятия
Структура ВС — это совокупность комплексируемых элементов и их связей. В качестве элементов ВС выступают отдельные ЭВМ и процессоры.
Существует большое количество признаков, по которым классифицируют вычислительные системы: по целевому назначению и выполняемым функциям, по типам и числу ЭВМ или процессоров, по архитектуре системы.
В 1966 году Майклом Флинном (Flynn) был предложен чрезвычайно удобный подход к классификации архитектур вычислительных систем [6]. В основу было положено понятие потока, под которым понимается последовательность элементов, команд или данных, обрабатываемая процессором. Соответствующая система классификации основана на рассмотрении числа потоков инструкций и потоков данных и описывает четыре архитектурных класса:
-
SISD = Single Instruction Single Data
Одиночный поток команд и одиночный поток данных. К этому классу относятся последовательные компьютерные системы, которые имеют один центральный процессор, способный обрабатывать только один поток последовательно исполняемых инструкций.
-
MISD = Multiple Instruction Single Data
Множественный поток команд и одиночный поток данных. Теоретически в этом типе машин множество инструкций должно выполняться над единственным потоком данных. До сих пор ни одной реальной машины, попадающей в данный класс, не было создано.
-
SIMD = Single Instruction Multiple Data
Одиночный поток команд и множественный поток данных. Эти системы обычно имеют большое количество процессоров, в пределах от 1024 до 16384, которые могут выполнять одну и ту же инструкцию относительно разных данных в жесткой конфигурации. Единственная инструкция параллельно выполняется над многими элементами данных.
-
MIMD = Multiple Instruction Multiple Data
Множественный поток команд и множественный поток данных. Эти машины параллельно выполняют несколько потоков инструкций над различными потоками данных. В отличие от многопроцессорных SISD-машин, упомянутых выше, команды и данные связаны, потому что они представляют различные части одной и той же выполняемой задачи. Например, MIMD-системы могут параллельно выполнять множество подзадач, с целью сокращения времени выполнения основной задачи.
Следует отметить, что хотя систематика Флинна широко используется при конкретизации типов компьютерных систем, такая классификация приводит к тому, что практически все виды параллельных систем (несмотря на их существенную разнородность) относятся к одной группе MIMD. Как результат, многими исследователями предпринимались неоднократные попытки детализации систематики Флинна. Так, например, для класса MIMD предложена практически общепризнанная структурная схема, в которой дальнейшее разделение типов многопроцессорных систем основывается на используемых способах организации оперативной памяти в этих системах [7].

Рисунок 1 — Структурная схема для класса MIMD
Кластер представляет собой два или больше компьютеров (часто называемых узлами), объединяемых при помощи сетевых технологий на базе шинной архитектуры или коммутатора и предстающих перед пользователями в качестве единого информационно-вычислительного ресурса. В качестве узлов кластера могут быть выбраны серверы, рабочие станции и даже обычные персональные компьютеры. Преимущество кластеризации для повышения работоспособности становится очевидным в случае сбоя какого-либо узла: при этом другой узел кластера может взять на себя нагрузку неисправного узла, и пользователи не заметят прерывания в доступе.
Кластеризация может быть осуществлена на разных уровнях компьютерной системы, включая аппаратное обеспечение, операционные системы, программы-утилиты, системы управления и приложения. Чем больше уровней системы объединены кластерной технологией, тем выше надежность, масштабируемость и управляемость кластера.
Модель однородного кластера с совместным использованием дискового пространства
Одной из систем классификации кластерных систем является классификация по совместному использованию одних и тех же дисков отдельными узлами: кластеры с совместным и раздельным использованием дискового пространства [8].
В работе рассмотрена модель кластера с совместным использованием дискового пространства. Одна из разновидностей кластера с совместным использованием дискового пространства представлена на рис. 2. Упрощенная модель кластера с совместным использованием дискового пространства приведена на рис. 3. [9].

Рисунок 2 — Кластер с совместным использованием дискового пространства
(анимация: создана в программе — Mp GIF Animator, объем — 104 КБ, количество кадров — 5, количество циклов повторения — 10, размер — 398x399)
Реализация
Определяющими при распараллеливании алгоритма являются:
- количество узлов вычислительного кластера;
- количество процессов на кластере;
- способ размещения данных;
- методы коммутации.
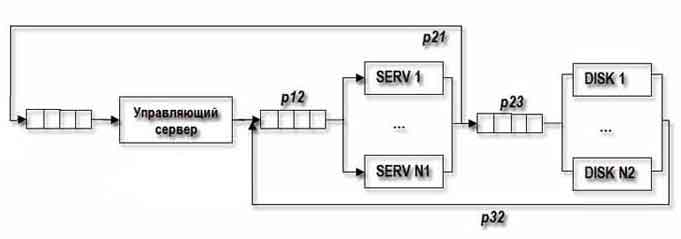
Рисунок 3 — Структурная схема кластера с совместным использованием дискового пространства.
В вычислительной системе, приведенной на рисунке 3, М задач или пользователей, N1 однотипных кластеров-серверов и N2 дисков, на которых хранятся данные. Каждый из М пользователей посылает с вероятностью P 12, запрос к одному из N1 серверов, которые, в свою очередь, обрабатывая этот запрос, обращаются к одному из N2 дисков с вероятностью P 23. Вероятность завершения обслуживания задачи одним из N2 дисков и поступление на i-й сервер тогда будет – P 32 [i = 1..N1].
Алгоритм
Алгоритм, примененный в параллельной реализации марковских моделей [2,10], состоит из двух частей: вычислений матрицы переходных вероятностей и вектора стационарных вероятностей.
Расчет стационарных вероятностей реализован с использованием итерационного алгоритма, в котором в качестве базового используется алгоритм умножения матрицы на вектор.

Рисунок 4 — Параллельный алгоритм расчета вектора стационарных вероятностей.
Вычисление элемента матрицы переходных вероятностей не зависит от соседних элементов, следовательно, в основе параллельной реализации этой части параллельного алгоритма можно использовать принцип распараллеливания по данным [4]. Суть заключается в том, в задаче выделены отдельные независимые части – ветви программы, которые при наличии нескольких обрабатывающих устройств могут выполняться параллельно и независимо друг от друга.
В качестве базовой подзадачи в алгоритме взят расчет строки матрицы переходных вероятностей, которая характеризуется одинаковой вычислительной трудоемкостью.
Рисунок 5 — Параллельний алгоритм построения матрицы переходных вероятностей.
Оценка эффективности
Вычисление основных характеристик происходит по следующим формулам:
 |
Среднее число свободных устройств в s-м узле вычисляется по формуле. |
 |
Среднее число занятых устройств в s-м узле определяется по формуле. |
 |
Загрузка устройств определяется по следующей формуле. |
 |
Среднее число задач, находящихся в s-м узле. |
 |
Среднее числo задач, находящихся в очереди к s-му узлу. |
 |
Среднее время пребывания в s-м узле. |
 |
Среднее время ожидания в s-м узле. |
 |
Среднее время пребывания в вычислительной системе. |
 |
Среднее время ожидания в вычислительной системе. |
Планируемые практические результаты:
Параллельный алгоритм марковских моделей многопроцессорных вычислительных систем позволяют моделировать любые многопроцессорные структуры. Эти алгоритмы можно использовать при анализе, синтезе и модернизации вычислительных структур. Они быстро вычисляются в масштабе реального времени и поэтому могут использоваться для реконфигурации вычислительных систем в режиме реального времени.
Вывод
В работе дано решение актуальной научной задачи, связанной с развитием методов и исследования параллельного алгоритма построения марковских моделей многопроцессорных вычислительных систем в корпоративных компьютерных сетях для анализа качества их функционирования, прогнозирования свойств и моделирования.
Использование параллельного алгоритма позволяет повысить эффективность исследуемой вычислительной структуры.
Предполагается исследование эффективности параллельного алгоритма построения марковской модели на параллельных структурах различной топологии с целью выяснения оптимальности параллельной вычислительной структуры.
Замечание! При написании данного автореферата магистерская работа еще не завершена. Окончательное завершение: декабрь 2010 г. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Литература
1. Основы вычислительных систем. Курс лекций. Модели и методы. [Электронный ресурс] / Интернет-ресурс. — Режим доступа: http://256bit.ru/education/infor2/lecture7-2.htm
2. Михайлова Т.В. Параллельный алгоритм построения дискретной модели Маркова // Искусственный интеллект. Интеллектуаьные и многопроцесорные системы. Материалы Международной научно-технической конференции, 25-30 сентября 2006г., Таганрог-Донецк-Минск, 2006. – С. 275–279
3. Мищук Ю.К. Моделирование параллельной реализации марковских моделей в многопроцессорных вычислительных системах // Наукові праці Донецького національного технічного університету. — Донецьк, ДонНТУ, 2010. – с. 238-240
4. Фельдман Л.П., Михайлова Т.В., Ролдугин А.В. Реализация параллельного алгоритма построения марковских моделей. // Наукові праці ДонНТУ. Серія: Інформатика, кібернетика та обчислювальна техніка, випуск 10. - С.17-20
5. Ефимов С.С. Обзор методов распараллеливания алгоритмов решения некоторых задач вычислительной дискретной математики. [Электронный ресурс] / Интернет-ресурс. — Режим доступа: http://cmm.univer.omsk.su/sbornik/jrn17/efimov.pdf
6. Image Processing. Классификация параллельных вычислительных систем. [Электронный ресурс] / Интернет-ресурс. — Режим доступа: http://iproc.ru/parallel-programming/lection-2/
7. Информационно-аналитический портал. Высокопроизводительные вычисления на WINDOWS-кластерах. Классификация вычислительных систем. [Электронный ресурс] / Интернет-ресурс. — Режим доступа: http://www.winhpc.ru/?id=36
8. Спортак М., Франк Ч., Паппас Ч. и др. Высокопроизводительные сети. Энциклопедия пользователя. — К.: ДиаСофт, 1998. — 432 с.
9. Фельдман Л.П., Михайлова Т.В. ВЕРОЯТНОСТНЫЕ МОДЕЛИ АНАЛИЗА ОЦЕНКИ ЭФФЕКТИВНОСТИ КЛАСТЕРНЫХ СИСТЕМ // Материалы второго Международного научно-практического семинара: Высокопрозводительные параллельные вычисления накластерных системах,Нижегородский государственный университет им. Н.И. Лобачевского, 2002. C. 307-314
10. Фельдман Л.П., Михайлова Т.В. Использование аналитических методов для оценки эффективности многопроцессорных вычислительных систем. //Электронное моделирование, Т.29, №2, 2007. - С.17-27
